Well written programs are modular, meaning that they are composed of separate parts that can be used without looking at the details of the code (the implementation). That is, a module can be understood in terms of what it does rather than how it does it. We have seen that well written functions can have this property, and last week started looking at structures and signatures as a way of writing modular code at the level of data and a set of functions that operate together, rather than just at the level of single functions.
If the code itself is not to form the description of what a module does, then we must have some other means of describing modules. Signatures are one way of describing what a module does without specifying its implementation, by providing a list of all the types, exceptions, variables and functions of the module without providing any code. However this still forms are an incomplete specification of what a module does. While there have been efforts at formal specification languages that precisely characterize what modules do, in practice programmers must make judicious use of comments and documentation to describe the modules of a system. It is crucially important that as the specifications of a module change, this documentation changes (as many others may depend on it. Thus it is good practice for this documentation to be in the code itself, and be in a special part of the code where programmers know to be particularly careful to check and change comments when they change code.
In SML comments about what a module does go in the signature, and when changing a signature one should be particularly careful to make corresponding changes to the comments. A good thing is that a well defined signature rarely needs to change, whereas its implementation may change more frequently.
Suppose we are implementing an abstraction for a finite set of natural numbers. The interface might look something like this:
signature NATSET = sig (* a "set" is a finite set of natural numbers: e.g., {1,12,0}, {}, {1003} *) type set (* empty is the empty set *) val empty : set (* single(x) is the set {x}. Requires: x >= 0 *) val single : int -> set (* union is the set union of two sets. *) val union : set*set -> set (* intersection is set intersection of two sets. *) val intersection : set*set -> set (* contains(x,s) is whether an element x is a member of set s *) val contains: int*set -> bool (* size(s) is the number of elements in s *) val size: set -> int end
In a real signature for sets of natural numbers we might want
additional operations such as map and fold, but let's
keep this relatively simple. Note that at the top of the signature definition is
a comment describing the overall data abstraction. Each declaration in the
signature has a comment that describes what that value or function is, but not
how it works. The only function that can create a set from an integer is
single, this function is commented to note that it is required that
its argument be non-negative, as only natural numbers can be stored in these
sets. These comments together with the definitions in the signature form
the specification of what the data abstraction does.
A simple implementation of NATSET would be to use singly-linked lists (the
built-in lists in SML):
structure NatSet :> NATSET = struct (* NATSET's as lists of non-negative integers that may contain duplicates *) type set = int list val empty = [] (* Enforce non-negativity of elements when creating a set*) fun single(x) = if x<0 then raise Fail "Natural numbers are non-negative" else [x] fun contains(x,s) = List.exists (fn y => x=y) s fun union(s1,s2) = s1@s2 fun intersection(s1,s2) = List.filter (fn (x) => contains(x,s2)) s1 (* Account for possible duplicates when computing set size*) fun size(s) = case s of [] => 0 | h::t => size(t) + (if contains(h,t) then 0 else 1) end
This implementation has the advantage of simplicity, although its performance will be poor for large sets. In particular, determining the size of a set is O(n2) time for n elements and intersection is O(mn) time for two sets of size m and n. Today we are focusing on defining abstract data types more than on their implementations so will settle for things that work even if they are somewhat inefficient. If the sets are always small, it might not even be worth writing an implementation that is more efficient. Having used a data abstraction that hides the implementation, we are free to write such a better implementation later, when it becomes clear its a performance issue.
Notice that the types of the functions aren't written down in the implementation; they aren't needed because they're already present in the signature, just like the specification comments that are also in the signature and don't need to be replicated in the structure.
How do we know
whether this implementation of NatSet satisfies its interface NATSET?
First, SML requires that the structure define all the types, functions and
values specified in the signature. However, we also need to know that this
implementation, which provides a particular "how", meets the specification in
the comments that describe NATSET.
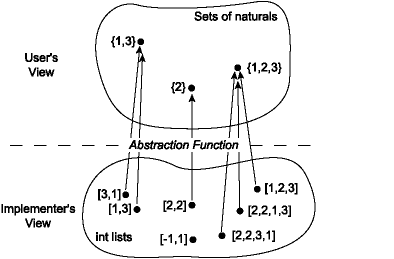
One useful way of thinking about implementations of data abstractions is in
terms of an abstraction function A,
that maps from values of the concrete (implementation) type to those of
the abstract (specification) type. It should be possible to
represent every valid value of the abstract type using a value of the concrete
type (A should be onto).
However, it need not be the case that every concrete value have a corresponding
abstract value (A can be a partial
function). Nor need it be the case that there is a single concrete value
for each abstract one (A can be
many-to-one). Our implementation of NatSet has the following
abstraction function,

One might express this abstraction function in English as:
"The list [a1, ..., an]
represents the smallest set that contains all the elements a1, ..., an.
Note the list may contain duplicates. "
The latter note is not strictly necessary, but helps make it clear that there
are multiple possible lists corresponding to the same set.
When there are values of the concrete type that do not correspond to any
values of the abstract type (a partial abstraction function), the implementation
must not allow such values to be created by the user of the abstraction.
Similarly, when there are multiple values of the concrete type that can
correspond to a single value of the abstract type (a many-to-one abstraction
function), the implementation must ensure that such values appear to be
identical from the user's point of view. Both of these are potential
sources of subtle bugs, and so care must be taken. Our implementation of
NatSet is both partial and many-to-one. Note that the comments in
the implementation address each of these cases. The only operation that
can create sets from numbers is in the function single, so it
ensures that negative numbers cannot be used (partial function). The only
operation that can distinguish between single and duplicate occurrences of the
same element of a set is size, and so it ensures that it handles
duplicates (many-to-one).
Additional constraints beyond the abstraction function are often referred to
as representation invariants, or rep invariants for short. They
specify restrictive properties of the concrete type that must hold in order for that type to correctly
represent the abstract type. For NatSet the requirement:
"The list [a1, ..., an] contains
no negative numbers."
is such a rep invariant. Rep invariants and abstraction functions are both
often useful for thinking about an implementation of a data abstraction.
Note that representation invariants specify restrictive properties that must
hold true for values of the concrete type. This often helps for instance
here in keeping track of the non-negativity of the elements.
It is important to verify that data abstractions work properly, and careful reasoning such as we have done for NatSet should still be supplemented with testing. Good test cases often derive from the abstraction function and the representation invariants, as these suggest things that might go wrong with an implementation. More generally, tests often consider boundary or "boundary" cases. For instance, here we use 0 as an element, because this is the smallest allowable element. We also test that unions and intersections with duplicate and non-duplicate entries have the correct size.
A useful notion in testing is that of an assertion of some invariant property that should hold. A simple form of assertion simply raises an exception if some expression does not evaluate to true.
fun assert(e) = e orelse raise Fail "Failed assertion";
A more advanced form of assertion would allow one to also assert that an expression raises a particular exception. For instance, in order to verify that single works correctly we want to test that for a negative number it raises a Fail exception.
(* an element in one set is the union of the two *)
assert(NatSet.contains
(1,NatSet.union (NatSet.single(0), NatSet.single(1)))
=true);
assert(NatSet.contains
(0,NatSet.union (NatSet.single(0), NatSet.single(1)))
=true);
(* equal elements are not double counted *)
assert(NatSet.size
(NatSet.union (NatSet.single(1), NatSet.single(1)))
=1);
(* a union has size of both sets *)
assert(NatSet.size
(NatSet.union (NatSet.single(1), NatSet.single(2)))
=2);
(* intersection membership and sizes *)
assert(NatSet.contains
(1,NatSet.intersection (NatSet.single(1), NatSet.single(1)))
=true);
assert(NatSet.size
(NatSet.intersection (NatSet.single(1), NatSet.single(1)))
=1);
assert(NatSet.size
(NatSet.intersection (NatSet.single(1), NatSet.single(2)))
=0);
We will now turn to a slightly better implementation of the NATSET
data abstraction where rep invariants are a little more helpful. NatSet1
again represents a NATSET using a list, but this time with no
duplicates in the list. One might express the abstraction function as:
"The list [a1, ..., an] represents the set
that contains the elements a1, ..., an. "
and the representation invariant as:
"The list [a1, ..., an] contains no negative
numbers and no duplicates."
Note that the abstraction function for this implementation is one-to-one, and
that we are able to enforce that with a representation invariant that there be
no duplicates in the list.
structure NatSet1 :> NATSET = struct (* NATSET's as lists of non-negative integers with no duplicates *) type set = int list val empty = [] (* Enforce non-negativity of elements when creating a set*) fun single(x) = if x<0 then raise Fail "Natural numbers are non-negative" else [x] fun contains(x,s) = List.exists (fn y => x=y) s (* Ensure no duplicates when computing union *) fun union(s1, s2) = foldl (fn(x,s) => if contains(x,s) then s else x::s) s1 s2 fun intersection(s1,s2) = List.filter (fn (x) => contains(x,s2)) s1 fun size(s) = length s end
The initial comment describes the abstraction function and the representation invariants, additional comments note where each of the representation invariants are enforced.
Note that the rep invariant makes it easier to write code that is correct,
because it means that we don't have to write code that works for all possible
incoming concrete representations - only those that satisfy the rep invariant.
This is why NatSet1.union doesn't have to consider lists that
contain duplicate elements.
Rep invariants are also useful even when writing modules that are not easily considered to be providing abstract data types. Sometimes it is difficult to identify an abstract view of data that is provided by the module; the abstraction function can be expressed only approximately. A rep invariant can be useful even without an abstraction function, because it documents the possible representations that the code is expected to handle correctly. This is helps one understand how the code works, and also is useful in maintenance, because the maintainer can avoid changes to the code that violate the invariant. One way to think of the rep invariant is that it is a contract between the implementer and him or herself (or themselves if there are multiple ones). In contrast the specification for the abstract data type is a contract between the implementer and the user. Just as it is not always easy to come up with good data abstractions and good implementations, it is also not always easy to come up with good representation invariants. However, they can be useful for writing and maintaining bug free code.
A third possible implementation of NATSET is in terms of binary
vectors that indicate the presence or absence of each element. The
abstraction function for this representation might be written:
"The Boolean vector v represents the set of all
natural numbers i such that sub(v,i)=true."
Note that this representation is a total rather than a partial function, as there cannot be any values
of the concrete type that do not correspond to values of the abstract type
(the index of a vector is non-negative).
structure NatSet2 :> NATSET = struct (* NATSET's as boolean vectors indicating presence or absence of * each element *) type set = bool vector val empty:set = Vector.fromList [] (* Raise a more reasonable error for negative numbers *) fun single(x) = if x<0 then raise Fail "Natural numbers are non-negative" else Vector.tabulate(x+1, fn(y) => x=y) fun contains(x,s) = x >= 0 andalso x < Vector.length(s) andalso Vector.sub(s,x) fun union(s1,s2) = let val len1 = Vector.length(s1) val len2 = Vector.length(s2) fun merge(i) = (i < len1 andalso Vector.sub(s1, i)) orelse (i < len2 andalso Vector.sub(s2, i)) in Vector.tabulate(Int.max(len1, len2), merge) end fun intersection(s1,s2) = let val len1 = Vector.length(s1) val len2 = Vector.length(s2) fun merge(i) = (i < len1 andalso Vector.sub(s1, i)) andalso (i < len2 andalso Vector.sub(s2, i)) in Vector.tabulate(Int.min(len1, len2), merge) end fun size(s) = Vector.foldl (fn (b,n) => if b then n+1 else n) 0 s end
You may be able to think of more complicated ways to implement sets that are (usually) better than any of these three. We'll talk about some alternative set implementations soon.
An important role of specification is to enable local reasoning. A
module together with a specification of what it does allows someone to use the
module without looking at the rest of
it (its implementation). We can also judge whether the rest of the program works
just based on this specification, and without
looking at the code of the module. However, we cannot generally reason locally about the
individual functions in module implementations. The problem
is that we don't have enough information about the relationship between the
concrete types (e.g., int list, bool vector) and the
corresponding abstract type (e.g., set). This lack of information
can be addressed by adding two new kinds of comments to the implementation: and abstraction
function and a representation invariant for the data type.
It is important to note that a strong rep invariant is not always the best choice, because it restricts future changes to the module. As we saw in the simple case of enforcing no duplicates in a list, operations may be implemented assuming that that the rep invariant holds for the input. If the rep invariant is ever weakened (made more permissive), some parts of the implementation may break. Thus, one of the most important purposes of the rep invariant is to document exactly what may and what may not be safely changed about a module implementation. A weaker rep invariant forces the implementer to work harder to produce a correct implementation, because less can be assumed about concrete representation values, but conversely it gives more flexibility for future changes to the code.