Problem Set 3: LZW Compression

Due Thursday, October 5, 2006, 11:00 pm.

Sep 23: Two executable files exe.x86-win32 (for Windows) or exe.x86-linux (for Linux) are now available for you to run the compression/decompression algorithms and see the expected output. To run an SML executable, type at the command prompt: "sml @SMLload=exe.x86-<os> <XY> <input> <output>". where X is 'c' or 'd' (compress or decompress), and Y is 'f' or 'v' (fixed or variable code size). The maximum number of bits is 12. For instance, to compress file 'sample.txt' in windows, using variable code size, run "sml @SMLload=exe.x86-win32 cv sample.txt sample.bin". Note: the directory of the sml executable program must be in your path.

This problem several parts. You will write your solutions in the appropriate files and submit the files separately on CMS. To get you started, we are providing a zip file containing several files. You can edit the necessary files, and submit your solution using CMS when you have finished. Remember that non-compiles and warnings will receive an automatic zero.

You will compile multiple structures at once using the Compilation Manager (CM).  We provided a file sources.cm that contains a list of all files that need to be compiled.  Use the compilation manager by typing CM.make(); at the command prompt. This command will automatically compile all of the programs that have changed since the last time CM was invoked.

For this assignment you will be working with a partner; you may use the code of either partner in doing this problem set (but not the code of anyone else).

[Download the zip file ps3.zip]

Part 1: Maps

Consider first maps with integer key, implemented as lists of key-value pairs (i.e., an association list). To avoid traversing the entire list when looking up a key that is not mapped, the implementation will maintain the list sorted. Furthermore, the map will keep the map size in a separate field so that it can return it without traversing the entire list. The type that describes polymorphic maps from integers to values of arbitrary types is:

type 'a map = (int * 'a) list * int

We have provided specifications in the file map.sig and an implementation of the lookup  function get in the file listmap.sml. Your tasks for this part include the following:

1. Write the appropriate description of the representation invariant (RI) and the abstraction function (AF).
2. Write the repOk function that raises an exception if the given structure is not well-formed, and returns it unchanged otherwise.
3. Finish the implementation of the functions that implement the map functionality.

To do: submit the file listmap.sml.

Part 2: Tries

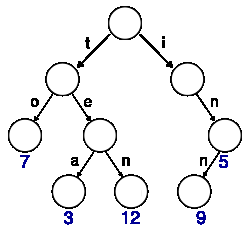
A trie is a tree structure whose edges are labeled with the elements of the alphabet. Each node can have up to N children, where N is the size of the alphabet. Nodes correspond to strings of elements of the alphabet. More precisely, each node corresponds to the sequence of elements traversed on the path from the root to that node. The map binds a string s to a value v by storing the value v in the node of s. The advantage of this scheme is that if efficiently represents common string prefixes, and lookups or inserts are achieved using quick searches starting from the root.

Suppose we want to build a map from strings of ASCII characters to integer codes. In this case, edges are labeled with ASCII characters, and integer codes are stored in (some of) the nodes. Here is an example: 

The above trie describes the map {"to"->7, "tea"->3, "ten"->12, "in"->5, "inn"->9}. The values (shown in blue) are stored in the nodes. Note that nodes might not have values. For instance the node that corresponds to string "te" doesn't have a value. Hence, "te" is not in the map.

It is sometimes useful to define a cursor pointing into the trie, in order to cache the last search in the trie and advance the cursor one step at a time.

In this part you will implement tries that map strings of integers (int list) to values of arbitrary types ('a). It is strongly recommended  that you build on the code from the previous part, and implement the outgoing edges from each node using a map of integers. For this, we have defined the trie using a functor that takes a MAP argument:

functor TrieFn(M: MAP): TRIE = struct
    ... 
end

Your task is to do the following:

1. Interface specifications. Before you begin implementing the trie data structure, you need to finish its specifications in the signature TRIE. The existing specifications may be incomplete, incorrect, or nonexistent.
    
2. Representation. You must decide how you will represent a trie. Briefly inspect the functions below to decide if certain pieces of information would make their implementation simpler. Then define an appropriate trie type.

   type 'a trie = (* your implementation here *)

3. Next to the representation type write a comment giving the abstraction function and representation invariant for tries.
    

4. Implement the function repOK. If the input trie satisfies the representation invariant, then repOK simply returns the input trie.  Otherwise, repOK raises Fail.

 
5. Trie operations. Implement the empty value, representing an empty trie. Then implement the functions put, get, size, and tabulate. The put function adds a new mapping to a trie. If the value to be inserted is associated with a list of integers that already exist in the trie, then the code should raise an exception ElementExists. The function get returns the binding of a string in the trie. If the string does not exist in the trie, then an exception NotFound must be raised. Finally, the function size returns the size of a trie; and tabulate(n,f) creates a new trie with n bindings, where binding k is f(k), for k between 0 and n-1.

   val empty: 'a trie
   val put: 'a trie * int list * 'a -> 'a trie
   val get: 'a trie * int list -> 'a
   val tabulate: int * (int -> int list * 'a) -> 'a trie
   val size: 'a trie -> int

   Note: the functions that build new tries are important since the course staff will use them to generate the inputs for testing other functions. Therefore, be careful to implement them correctly.
    

6. Cursor support. Next, define an appropriate type to describe a cursor into a trie structure. Make sure the type contains enough information to support the cursor operations defined below.

   type 'a cursor = (* your implementation here *)

   Implement the following functions:

   val cursor: 'a trie * int list -> 'a cursor
   val advance: 'a cursor * int -> 'a cursor option
   val getc: 'a cursor -> 'a option
   val putc: 'a trie * 'a cursor * int * 'a -> 'a trie

   The function cursor returns a cursor positioned at the node that corresponds to the string given as argument. In the string doesn't exits, the exception NotFound is raised. The function advance moves the cursor one position down the tree, following the edge that corresponds to the value passed as an argument. This function returns NONE if no such edge exists. The function getc yields the value stored at the node that the cursor points to. Finally, putc(t,c,x,v) advances cursor c along the edge x (creating the edge if it doesn't exit), inserts value v at that position in trie t, and returns the updated trie. The appropriate exception is raised if a value already exists at the insertion point.
   

Part 3: The LZW Algorithm

Ordinary files (both binary and text files) consist a sequence of characters, where each character is represented using an 8-bit ASCII code. However, this representation fails to take advantage of repeated sequences of characters. For example, the string “of the” occurs very frequently in written English. Thus, it would be very useful to encode “of the” using fewer than 6 bytes = 48 bits (one byte per character).  The LZW algorithm proposed by Lempel and Ziv in the late '70s, and then enhanced by Welch in the '80, is a widely used compression method that automatically identifies such recurring strings and compactly encodes them using integer codes.

The algorithm has two parts: the compression and the decompression algorithms. To simplify the presentation of these algorithms, consider for now a scheme where all codes have a fixed number of bits. For instance, the compression outputs a sequence of 12-bit codes; and decompression reads in a sequence of 12-bits codes.

Dictionaries are the key data structures in both algorithms. The compression part grows a map from strings of bytes to their codes, and the decompression part grows the inverse map, from the codes being read to their associated strings. The structures you have implemented in the previous parts are good matches for these dictionaries. The nice thing about LZW is that it doesn't need to store the dictionary in the output file: the dictionary is automatically reconstructed during the decompression phase!

Compression Algorithm

prefix <- ""
loop:
  read next input byte c
  if D contains prefix + c then
     prefix <- prefix + c
  else
     output code D(prefix)
     insert (prefix + c) into D
     prefix <- c

output code D(prefix) 

At each iteration the algorithm appends the new character to the current prefix, and checks whether the resulting string is in the dictionary. If not, it outputs the code of the previous prefix, and inserts the new prefix in D. At the end, the code of the last prefix is printed out.

Example: consider the text "AND_BANANAS". Here is how the compression algorithm works for this string. We use the notation [X] for output (e.g., 12-bit) codes. If X is a character, [X] is its ASCII code; if X is a number, [X] is the code X itself.

Decompression Algorithm

During decompression, the algorithm maps codes back to strings of integers. The decompression dictionary D' is initializes to map each code c between 0 and 255 to the string containing just c. For instance, 65->"A". As it runs, the algorithm remembers the last string being printed out, called prev in the pseudo-code below.

read code c
output string D'(c)
prev <- c
loop:
  read next code c
  lookup string s <- D'(c)
  if s not found then s <- prev + first(prev)  
  write string s
  insert prev + first(s) into D'
  prev <- s

In this pseudo-code, first(s) represents the first character of string s. The dictionary D' constructed during decompression is the inverse of the dictionary D constructed during compression. The entries in D' are added in the same order as the corresponding entries in D.

The if statement in the code above treats the special case where the algorithm looks up the code that is just about to be inserted; although the string of that code is not known, the first character is known and that is what makes the algorithm work. The table below illustrates the functioning of the decompression algorithm for the above example. The special situation mentioned above occurs in the line before the last.

Algorithm Variations

So far, we have assumed a simple model where the codes in the compressed file have a fixed size S. This model makes it easy for the decompressor to get the next code at each step, by reading the next S bits. However, for small files this can actually cause an increase in file size. In the example above, the "compressed" text has 8*12 =96 bits, whereas the original text has only 11*8 = 88 bits.

A better scheme is to use variable bit size: start with 8 bits and increase the bit size as the algorithm proceeds. Of course, the compressor and decompressor must be in synch regarding the bit size. The solution is to use as many bits as needed to represent the current code (which can be derived from the dictionary size, since dictionaries only grow). For compression the current code is the number in the "Insert to dictionary" column minus one; for decompression it is the number in the "Insert to dictionary" column.  In the above example, the first "A" uses 8 bits, and the remaining codes use 9 bits. We suggest you first implement the algorithm for fixed bit sizes, and then extend it to support variable bit sizes.

Another concern is what needs to be done when the dictionary becomes full (i.e., codes reach the maximum number of bits). In this assignment, you will stop adding new codes to the dictionaries when they become full. (Other alternatives include emptying the dictionary, allowing to accumulate new string patterns; or keeping around the frequently used codes, and dropping the others). 

Your LZW algorithm will be parameterized on: 1) a boolean flag indicating fixed or variable size; and 2) an integer (greater than 8) denoting the maximum code size in bits. Once this size is reached, the dictionaries remain unchanged. The parameterization is achieved using a functor LzwFn(S:SCHEMA). The signature SCHEMA defines the two parameters. Check the file test.sml to see how to instantiate different schemas and run compressing and decompressing tests.

The structure BinIO in the Basis Library provides the necessary functionality for manipulating binary files. Bytes read and written when accessing binary files are represented as Word8.word (essentially, unsigned 8-bit integers). Furthermore, to help you with reading and writing  bit sequences, we have provided a BitIO structure (in files bitio.sig and bitio.sml). Note that, unlike the corresponding function in BinIO, the input and output functions in BitIO are written in a functional style: they return the new file handle (called stream) after each I/O operation. Don't forget to capture the resulting value and use it for the subsequent I/O operations!

To do: Implement compress and  decompress in lzw.sml.

Part 4: Proof by Induction

fun findMiddle(l) =
  let
    fun help(m, l') =
      case (m,l') of
        (x::xs,[]) => x
      | (x::xs,[y]) => x
      | (x::xs,y::y2::ys) => help(xs, ys)
      | _ => raise Fail "SML is broken"
  in
    case l of
      [] => raise Fail "Can't find the middle of an empty list"
    | x::xs => help(l,xs)
  end

Prove that findMiddle(l) correctly finds the middle  of a non-empty list l.  Make sure you include all parts of the proof and to clearly label each part. The middle element of a list with n elements is the element at index ceil(n/2) -1, where indices start at 0.

To do: turn in the solution to part 3 in the file induction.txt.

Bonus Points: Higher-order fun

The following problem will count for 5 bonus points (the total max is still 100). Consider the following four higher-order functions.

fun peel f x = (f (x div 10) (x mod 10))
fun sub f x y = (f (Int.abs(y*y-x)))
fun swap f x y = (f y x)
fun dummy x = x

We can think of these four functions as basic building blocks, and construct new functions with them, without using any operators, literals, constants, keywords, functions, etc. For instance, we can define "val magic = peel(sub dummy)".  The problem asks you to write three magic expressions magic1, magic2, and magic3 that will yield the values indicated below.  For each answer, provide a high-level explanation (i.e., not the step-by-step evaluation) why they produce the desired results:

magic1 32 = 7
magic2 4 = 5 
magic3 151 = 15 

Turn in the solution in the file hofun.sml.