Introduction
Pattern matching of strings is a frequently used primitive operation. The first pass in a compiler uses pattern matching to group individual characters into lexically meaningful groups such as identifiers and numbers. Many applications and tools generate regularly formatted textual output. Textual pattern matching is essential for programmatically detecting and extracting information from such textual output.
One might imagine implementing a custom pattern matcher for each string processing problem, a time consuming and error prone procedure. Fortunately, theoretical computer science results provides several elegant yet simple formulations of the pattern matching problem which yield immediate practical benefits.
In this recitation, we will discuss two such practical pattern matching systems: deterministic finite automata (DFA) and regular expressions. Each system provides a formal, structured way of specifying a pattern to recognize. Given a string and a DFA or regular expression specification, there exists natural and reasonably efficient algorithms to specify determine whether the given string matches the given specification.
While the two appear to be very different, they turn out to be equivalent in expressive power: every DFA has an equivalent regular expression, and vice versa.
Here, we will focus on how to interpret DFAs and regular expressions; see CS 381/481/682, or Sipser's Introduction to the Theory of Computation for the DFA/regular expression equivalence proofs. These theorems are constructive, meaning that they precisely show how to convert one to the other, and thus specify algorithms for performing this conversion.
Deterministic Finite Automata
You have already seen deterministic finite automata (DFA) in Problem Set 2. Here, we generalize DFAs to arbitrary inputs, not just strings over the alphabet { a, b} . DFA descriptions are of the following form:
- A set of states. For an automaton with n states, we will denote states with all numbers from 1 to n
- A start state
- A set of final (accepting) states
- A transition function (see below).
DFA specifications describe the behavior of a machine on a character-by-character basis. A DFA is given an input string, which is read one character at a time.
Whenever the DFA reads a character (and only then), the automaton moves from its current state p to a "next" state q. State q depends on both state p and on the character read in input. The moves from one state to the next as a result of reading an input character are described by the transition function. Given any state and any character that can appear in the input, the transition function specifies the next state.
A DFA accepts an input string s if and only if the automaton ends up in a final (accepting) state after reading the entire input string.
The DFA implementation presented here is more efficient than the one from PS2. Recall that PS2 defined the transition function with a list. Each time an input symbol was processed, the list was scanned for the current state and the current input symbol. Hence, the running time per input symbol was linear in the number of states. Once the string is finished, the matching algorithm needed to scan through the list of accept states to see whether the current state was an accept state.
One way to improve performance is to reduce the cost of these lookups using more efficient data structures, such as a binary search tree or an array. We will use arrays here.
The transition function maps (state, input_symbol) tuples to states. This precisely matches the lookup operation of a two-dimensional array. We map the state, which is an integer, into the first dimension, and the ordinal, or numerical value, of a Char into the second dimension. We will need a S - by - C array, where S is the number of states, and C is the number of ordinals. The list of accept states can be thought of as a function mapping states to boolean values, where the function is true if the state is an accept state, and false if the state is not an accept state. To encode this function, we will need a S-long one dimensional array.
The number of states is available from the DFA description, and the largest ordinal is Char.maxOrd + 1, since the ordinals start at 0 and go up to Char.maxOrd. Thus, the first step is to allocate an Array2 to store the transition table, and an Array to store the accept state table. Once the arrays are instantiated, update is called to initialize the arrays to the appropriate values corresponding to the DFA.
Note that the transition table is stored as an Array2 of datatype dest. It is often possible to detect that a string cannot possibly match the language of a DFA. For instance, this can occur if the DFA accepts only strings consisting of {0, 1}, but the input contains letters. We handle this case specially by encoding these transitions as Error values in the transition table.
Note that this is only an optimization and does not increase the expressive power of a DFA. Rather than directly encoding such transitions, we could instead force all transitions to a "junk" state m, which is not an accept state, and which transitions back to m on all symbols. Once the DFA enters such a state on a prefix of a string, it can never escape state m, and therefore will not accept the string.
The structure of the matching algorithm closely matches that of the list representation. The string is processed one character at a time, from left to right. The induction variable pos keeps track of the current position in the array, and state tracks the current state. At each position, the transition Array2 is indexed with the state and current input symbol in to yield the next state. Once the string is fully processed, the final state is checked against the accept table to see whether the input should be accepted or rejected.
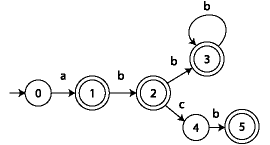
a b c accept ============== 0 1 - - F 1 - 2 - T 2 - 3 4 T 3 - 3 - T 4 - 5 - F 5 - - - T
Here is the code that implements DFAs:
type state = int (* Note: 0 is the start state *)
datatype dest =
State of state (* Edge destination is another state *)
| Error (* if no next state *)
type DFA = {table: dest Array2.array, accept: bool Array.array}
(* Check whether the DFA "pattern" accepts "text" *)
fun search({table, accept}: DFA, text: string): bool =
let
(* Give the next state of the DFA, assuming that it is in
* state "state" and the next character is text[pos]. *)
fun next_state(pos: int, state: int): dest =
let
val char = Char.ord(String.sub(text, pos))
in
Array2.sub(table, state, char)
end
(* Walk the DFA down the string "text" from position "pos",
* returning whether it accepts the rest of the string. *)
fun search(pos: int, state: int): bool =
if pos = String.size(text)
then Array.sub(accept, state)
else case next_state(pos, state) of
Error => false
| State(s) => search(pos + 1, s)
in
search(0,0)
end
(* Create DFA shown in the diagram and table above. *)
- val nbOfStates = 6;
val nbOfStates = 6 : int
-
- val table = Array2.array(nbOfStates, Char.maxOrd + 1, Error);
val table = - : dest Array2.array
-
- Array2.update(table, 0, Char.ord(#"a"), State 1);
val it = () : unit
-
- Array2.update(table, 1, Char.ord(#"b"), State 2);
val it = () : unit
-
- Array2.update(table, 2, Char.ord(#"b"), State 3);
val it = () : unit
- Array2.update(table, 2, Char.ord(#"c"), State 4);
val it = () : unit
-
- Array2.update(table, 3, Char.ord(#"b"), State 3);
val it = () : unit
-
- Array2.update(table, 4, Char.ord(#"b"), State 5);
val it = () : unit
-
-
- val accept = Array.array(nbOfStates, false);
val accept = [|false,false,false,false,false,false|] : bool array
-
- Array.update(accept, 1, true);
val it = () : unit
- Array.update(accept, 2, true);
val it = () : unit
- Array.update(accept, 3, true);
val it = () : unit
- Array.update(accept, 5, true);
val it = () : unit
-
(* Test the DFA on various strings. *)
- search({table = table, accept = accept}, "");
val it = false : bool
-
- search({table = table, accept = accept}, "a");
val it = true : bool
-
- search({table = table, accept = accept}, "b");
val it = false : bool
-
- search({table = table, accept = accept}, "abbbbbbb");
val it = true : bool
-
- search({table = table, accept = accept}, "abcb");
val it = true : bool
-
- search({table = table, accept = accept}, "abcba");
val it = false : bool
-
Regular Expressions
Regular expressions provide a high-level description syntax for specifying patterns. Regular expressions consist of pieces of text that are interspersed with operators that specify how those pieces relate to one another in a matched string. One can think of regular expressions as a small programming language. The regular expression syntax allows programmers to express patterns as operations on pieces of text, instead of with state-by-state, character-by-character actions.
In the examples below, we will use only "a" and "b" as symbols in the regular expression.
Parenthesis may be used in arbitrary locations in regular expressions. They denote grouping, just as in arithmetic expressions.
A character is the most basic regular expression. It matches itself. For instance, the regular expression
a
accepts the language
{ "a" }
. (period) is a special character that accepts any symbol.
In fact, characters and . are the only elements in regular expressions that explicitly match text.
Concatenation is the most commonly used operator. Two regular expressions e0 and e1 are concatenated simply by being next to each other. A string s = s0 s1 (s1 followed by, or concatenate, s0) is accepted by a concatenated expression e0 e1 if and only if e0 accepts s0 and e1 accepts s1.
For instance, the regular expression
ab
is composed of the regular expressions a and b, and matches the string
"ab"
Similarly, the regular expression
abc
matches the string
"abc"
Note that there are multiple ways to interpret regular expression abc: as the concatenation of ab and c, or the concatenation of a and bc. Since concatenation is associative, either interpretation is fine. However, we will see later that the regular expression grammar will unambiguously choose a bc.
The ? operator is appended to a regular expression. It signifies optional, or "zero or one". e ? matches either a string that matches e, or the empty string "". Note that once we introduce this non-associative operator, grouping becomes important. For instance,
''a(a)?''
matches "a" and "aa", whereas
''(aa)?''
matches "" and "aa".
The | operator is an infix operator that joins two regular expressions. It signifies "either or". Hence, e1 | e2 accepts "s" if either e1 or e2 accepts "s". For instance "(a*)|(b*)" matches any string consisting 0 or more 'a,' or any string consisting of 0 or more 'b'-s.
The * operator is appended to regular expressions, just like the ? operator. It means "zero or more." Hence, if e matches a string "s", then e* matches "", "s", "ss", "sss", ... . Note that if e matches multiple strings, then e* matches any sequence of strings that matches e. Hence, (a|b)* matches "", "a", "b", "aa", "ab", "ba", ....
Just as in arithmetic expressions, operator precedence is important in regular expressions. * and ? have highest precedence. This means that aa? is equivalent to a(a?). In a departure from most regular expressions, | shares the same precedence as * and ?, and so ab|aba is equivalent to a(b|a)ba. In perl and extended UNIX regular expressions, | actually has lowest precedence, so the expression in question means (ab)|(aba).
Our definition simplifies the definition of the grammar by removing a precedence level. We have two precedence orders: in increasing order, they are
- concatenation
- *,?, |
In contrast, if | was lower than concatenation, then the precedence, in increasing order would be
- |
- concatenation
- *, ?
AST nodes, tokens
The datatype regexp represents the AST, and the datatype token represents the tokens.
Notice that the AST does not contain any factor or term nodes. At parse time, the abstract nodes are generated directly, with the extraneous concrete nodes, which are only needed for disambiguation, eliminated.
The tokens correspond to the textual elements of regular expression that are below the grammatic level of abstraction. In the case of regular expressions, each token is a single character, but it is possible to consider more complicated tokens, such as "escaped" parentheses \( or \). These would map to Literals with character values ( and ), respectively, rather than LParen and RParen, thus allowing the user to specify parentheses in her patterns.
Lexer
The lexer is defined in tokenize. tokenize converts the input string into a list of tokens. The translation is straightforward, except for spaces. Spaces are omitted, rather than converted. This is standard practice: while spaces may be critical during tokenization, such as to separate different identifiers, they are omitted from the actual token stream.
Match algorithm
The match algorithm is essentially an interpreter. The major divergence from the interpreters that you have seen before is that it is written using continuation passing style (CPS). The continuation is the helper parameter k, with type char list -> bool. Essentially, this type is the same as match, specialized with a regular expression. A continuation essentially encodes the how to handle the remainder of a computation.
Under a CPS, the helper can be interpreted as follows: match the left part of the input list cs with the regular expression. Then, call the continuation with the remainder. For instance, in the Char case, the next character is removed, and if the character matches, the continuation is called with the remainder of the string.
Note the following:
- In concatenation-like operations such as Concatenation and Star, a new continuation is created to capture the fact that after handling e1, e2 must still be matched. It is incorrect to call k directly, since it should not be called until after the string for the current regexp is fully matched.
- In operations where there are two choices, such as Or, Star, or Optional, the computation effectively branches in two. Both possibilities are evaluated, and if either matches, then there was a match. Note that this branching can dramatically increase the cost of evaluating the regular expression. There exist straightforward algorithms that rely on conversion to automata that don't have analogous decision points, and thus execute in polynomial time.
Regular Expression Grammar
Note: you do not have to understand in great detail how properties like precedence of the operators emerge from the specification of the grammar. You need to understand the grammar to the extent that you can understand what the code does.
Here is the regular expression grammar. Note that it is written to respect operator precedence, to be unambiguous, and to be parseable with a simple parser.
rexp = term Empty | term rexp term = factor | factor? | factor* | factor '|' term factor = <character> | . | (rexp)
Non-terminals (rexp,term,factor) that are listed higher have lower precedence than those that are listed lower. To see why, notice that it is impossible for ?, a highest precedence operator, to follow any expression other than a factor, namely a parenthesized expression or a single-character match (<character> or .).
The definition of rexp forces concatenation to group to the right (right associative). That is, aaa parses as a(aa). Note that the only term that can match multiple elements, namely rexp, falls to the right. As we shall see shortly, this design choice allows us to use a straightforward recursive descent parser.
The Empty token does not correspond to any textual input. It is added for technical reasons, to simplify the matching algorithm.
Note that this grammar generates a rather convoluted concrete syntax tree even for simple regular expressions.
- parse_rexp (tokenize (String.explode "a"));
val it = (Concat (Char #"a",Empty),[]) : regexp * token list
-
- parse_rexp (tokenize (String.explode "a*"));
val it = (Concat (Star (Char #"a"),Empty),[]) : regexp * token list
-
- parse_rexp (tokenize (String.explode "abc"));
val it = (Concat (Char #"a",Concat (Char #"b",Concat (Char #"c",Empty))),[])
: regexp * token list
-
- parse_rexp (tokenize (String.explode "a*b?(c|d)"));
val it =
(Concat
(Star (Char #"a"),
Concat
(Optional (Char #"b"),
Concat (Concat (Or (Char #"c",Char #"d"),Empty),Empty))),[])
: regexp * token list
-
- parse_rexp (tokenize (String.explode "(ab+)|(c?d*)"));
val it =
(Concat
(Or
(Concat (Char #"a",Concat (Char #"b",Concat (Char #"+",Empty))),
Concat (Optional (Char #"c"),Concat (Star (Char #"d"),Empty))),Empty),
[]) : regexp * token list
Recursive Descent Parser
We'll now discuss the actual implementation of the regular expression parser.
parse_rexp defines this parser. Unlike MiniML, which used an autogenerated parser, this parser is hand-coded. The parser is recursive descent: the code structure matches that of the grammar, modulo some factoring out of common functionality between different right hand sides. A parse routine is defined for each non-terminal rexp, term, and factor.
Each right hand side corresponds to a particular case in the corresponding parse routine. The right-hand sides are translated into sequential programs, left to right. Where a non-terminal occurs in the right hand side, the parse routine contains a call to the non-terminal's parse routine. Where a terminal occurs, it is removed from the input list.
Please note:
- The terminals are used to distinguish between the possible right hand sides
- When the code for a right hand side hits the end of the right hand side, it uses the next terminal to disambiguate a decision. This terminal is not consumed, since it doesn't actually occur in the right hand side. It actually occurs to the right of the non-terminal in another rule! This occurs in parse_rexp, with the RParen.
- The parse routines construct the abstract syntax tree.
Note that the function call below leads to an infinite loop. Do you understand why? Is it possible to enter a regular expression whose AST would be represented by Star Empty?
helper (Star Empty) [#"a"] (List.null)
And here is the code:
datatype regexp =
Empty (* matches the empty string *)
| Char of char (* Char(c) matches a string "c'" iff c = c' *)
| Any (* Any matches a string "c" for any c *)
| Optional of regexp
| Or of regexp * regexp (* Or(r1,r2) matches s iff r1 matches s or r2
matches s *)
| Concat of regexp * regexp (* Concat(r1,r2) matches s iff we can break
s into two pieces s1 and s2 such that r1
matches s1 and r2 matches s2. *)
| Star of regexp (* Star(r) matches s iff
Or(Empty,Concat(r,Star(r))) matches s.
That is, if zero or more copies of r
concatenated together matches s. *)
(* raised when we encounter a syntax error *)
exception SyntaxError of string
(* tokens processed by the parser *)
datatype token = Literal of char
| VertBar
| Asterisk
| QMark
| LParen
| RParen
| Period
(* convert list of characters into a list of tokens *)
fun tokenize (inp : char list): token list =
(case inp of
nil => nil
| (#"|" :: cs) => (VertBar :: tokenize cs)
| (#"." :: cs) => (Period :: tokenize cs)
| (#"?" :: cs) => (QMark :: tokenize cs)
| (#"*" :: cs) => (Asterisk :: tokenize cs)
| (#"(" :: cs) => (LParen :: tokenize cs)
| (#")" :: cs) => (RParen :: tokenize cs)
| (#" " :: cs) => tokenize cs
| (c :: cs) => Literal c :: tokenize cs)
fun parse_rexp (ts: token list): regexp * (token list) =
let
val (term, rest) = parse_term ts
in
case rest of
([] | RParen::_) => (Concat(term, Empty), rest)
| _ => let
val (exp, rest') = parse_rexp rest
in
(Concat(term, exp), rest')
end
end
and parse_term (ts: token list): regexp * (token list) =
let
val (factor, rest) = parse_factor ts
in
case rest of
QMark::tl => (Optional factor, tl)
| Asterisk::tl => (Star factor, tl)
| VertBar::tl => let
val (term, rest') = parse_term tl
in
(Or(factor, term), rest')
end
| _ => (factor, rest)
end
and parse_factor (ts: token list): regexp * (token list) =
case ts of
(Literal c)::tl => (Char c, tl)
| Period::tl => (Any, tl)
| LParen::tl => let
val (exp, rest) = parse_rexp tl
in
case rest of
RParen::tl => (exp, tl)
| _ => raise SyntaxError "parantheses not properly balanced"
end
| _ => raise SyntaxError "incorrect regular expression"
fun match (rexp: string) (s: string): bool =
let
fun helper (exp: regexp) (cs: char list) (k: char list -> bool): bool =
case (exp, cs) of
(Empty, _) => k cs
| (Char c, []) => false
| (Char c, c'::tl) => (c = c') andalso (k tl)
| (Any, []) => false
| (Any, _::tl) => k cs
| (Or(e1, e2), _) => (helper e1 cs k ) orelse (helper e2 cs k)
| (Concat(e1, e2), _) => helper e1 cs (fn cs' => helper e2 cs' k)
| (Star e1, _) => (k cs) orelse (helper e1 cs (fn cs' => helper exp cs' k))
| (Optional e, _) => (k cs) orelse (helper e cs k)
val (exp, _): regexp * token list = parse_rexp(tokenize (String.explode rexp))
in
helper exp (String.explode s) (List.null)
end
- match "a*" "";
val it = true : bool
-
- match "a*" "aaaaaaaaa";
val it = true : bool
-
- match "aa" "a";
val it = false : bool
-
- match "aa" "aa";
val it = true : bool
-
- match "aa" "aaaa";
val it = false : bool
-
- match "a*b?a" "aaaaaba";
val it = true : bool
-
- match "a*b?a" "aaaaa";
val it = true : bool
-
- match "(a*)|(b*)" "aaaaa";
val it = true : bool
-
- match "(a*)|(b*)" "bbb";
val it = true : bool