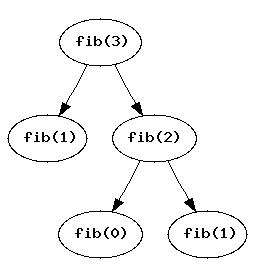
Figure 1: fib(3)
Consider the following code. Notice that the datatype that is defined is pretty much the same as the type used for normal lists, except a reference is used to refer to the tail of the list.
datatype 'a list = Empty | Node of 'a * 'a list ref val dummy = ref Empty: int list ref; val lst = Node(3, dummy); val () = dummy := lst; val lst2 = Node(1, ref (Node(2, ref (Node(3, dummy))))); val () = dummy := lst2;
This example shows a general way for creating loops in data structures. First initialize the reference to point to some garbage dummy value, and then update the reference to point back to the thing that contains it to "tie the knot."
Consider the following function for printing these lists:
fun printLst (l: int list): unit =
case l of
Empty => raise Fail "can not happen"
| Node(h, t) => (print (Int.toString h); printLst (!t))
Notice that this function will never halt if you attempt to print a circular list with it.
Consider the following implementation of the fibonacci function:
fun fib(n:int):int = if n = 0 then 1 else if n = 1 then 1 else fib(n - 2) + fib(n - 1)
The following call-graph shows the processing which results from fib(3):

Now consider the following picture representing the calls that from running fib(5):
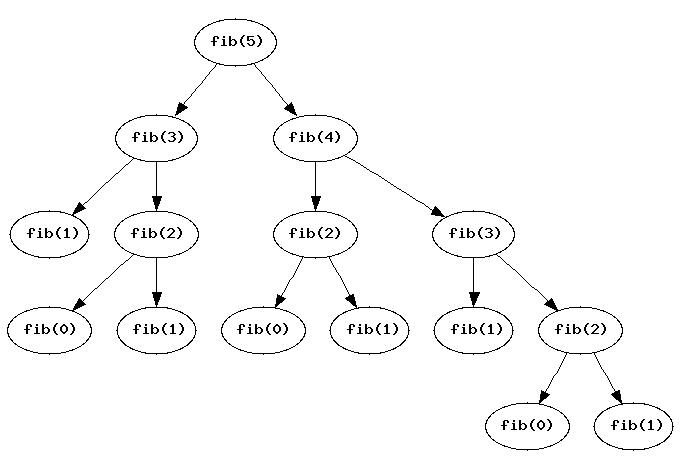
Notice that the subtree from figure 3 is recomputed twice. The subtree for fib(3) is recomputed even more times. If we were doing fib(6) or higher, we would see even more wasteful re-computation. It is inefficient to recompute these subtrees repeatedly; we should be able to remember the value of a call after the first time we compute it, so that we don't need to recompute the value again in the future. This is the intuition behind the memoization technique:
local
val known = Array.array(100, ~1) (* initialize all values to -1 *)
in
fun fibo(n:int):int =
if n = 0 then 1
else if n = 1 then 1
else if Array.sub(known, n) <> ~1 then Array.sub(known, n)
else (Array.update(known, n, fibo(n - 2) + fibo(n - 1));
Array.sub(known, n))
end
The base cases of remain the same. In what was previously the recursive case, we first check the array of known values to see if we have already computed this value. If so, we simply return it. Otherwise, we do recursion to compute it and store it in the known array for future use.
The local keyword may be new to you. It means that known is declared outside of fibo but is only visible to fibo. If known were declared inside of fibo, it would get reinitialized with every call, so all the references to known would point to different arrays.