Problem Set 2: Datastructures and polymorphism
Due on Monday, September 20, 12:01 am
Instructions
This assignment covers datastructures and polymorphism, and
provides more challenging practice with functional programming than
the previous assignment. Several of the problems can be solved
concisely using higher order functions from the Basis library such as
filter, fold, map, or find. Use of these is strongly encouraged.
As always, please start the assignment early, and be sure to see
the consultants in the lab or TAs during office hours if you encounter
difficulty. We suggest reading each problem in its entirety before
writing code, so that you can identify common functionality between
different requirements, and factor this helper functions.
There are three problems in this assignment, with several subproblems each.
Modify the .sml template files from ps2.zip. We will autograde your
homework, so do not modify the .sig files, and do not rename or change
the signatures of the variables or functions that we provide. The
autograder will directly access these name bindings.
Do not modify sources.cm, as it will not be submitted. Make sure
that your code compiles under CM with the provided sources.cm before
submitting! To compile the code with CM, change to the directory
containing your PS2 files, start SML, and evaluate
CM.make();
Non-compiling code will receive an automatic zero.
Unlike last time, you will submit each modified .sml file individually
through CMS.
Towers of Hanoi
The towers of Hanoi puzzle consists of three pegs, labeled A, B, and C,
and n discs, with no two discs being of the same size (radius). A peg holds a stack
of discs, and we identify discs with integer numbers 1, 2, ...,
n. The higher the
number, the bigger the radius of the disc. At each step, exactly one
disc is taken from a peg, and it is moved onto another peg subject to the constraint
that a bigger disc can never be placed over a
smaller disc. Any disc can be placed onto a peg if the peg has no disc
on it (is empty). Initially all discs are stacked on top of each other
in a correct configuration on peg A. The goal of the game is to move
all n discs from peg A onto peg B. This puzzle was originally invented
by Edouard Lucus, a French mathematician, in 1883.
The problem can be solved using the
following algorithm: To move a stack of k discs from peg A to peg B,
we first move k-1 discs from A to C, then move the remaining (kth)
disc from peg A to B, and then finally move all k-1 discs on C to
B. Now, how do we move k-1 discs from peg A to C, as
the first step above requires? We simply repeat
this algorithm recursively: to move k-1 discs from A to C we first move
k-2 discs from A
to B, then move the top remaining disc (the (k-1)th disc) from A to C. Then
we move k-2 discs from peg B to C. There are now k-1 discs on C.
In this assignment you will write a structure capable of solving
instances of the Tower of the Hanoi problem.
Part 1 : Creating a simple stack
First implement a simple stack in stack-student.sml. A stack is a
LIFO (Last in, First out) data structure that grants access to only a
single element at a time (the topmost element). New elements added to
the stack are placed on the top, and elements taken from the stack are
removed from the top. We will use a list of integers to represent a
stack, with the topmost element at the front of the list. Also, we
will represent discs as integers storing their radii ("size").
More formally, we will use the following type definitions:
type disc = int
type stack = int list
type peg = string * stack
type towers = peg * peg * peg
type move = disc * string * string
Note that the type declaration does not create a new type, it just
gives a new, more convenient name to another type.
You must carefully implement the following functions (whose types are also
given in stack.sig, a file that you should NOT modify in any way):
empty : stack
Returns a stack with no elements.
height : stack -> int
Returns the number of elements in the stack.
isEmpty : stack -> bool
Returns true if the stack is empty.
push : stack * disc -> stack
Puts the specified disc on the top of the stack.
pop : stack -> disc * stack
Removes the topmost element of the stack, and returns it together with the
'leftover' stack.
top : stack -> disc
Returns the topmost element of the stack without removing it.
Be sure your stack works properly and comprehensively before
continuing on to the next part. Think of all special cases that might arise!
Part 2 : Solving the Towers of Hanoi
Now you will use the stack you have implemented to implement the
solution algorithm discussed above. We have defined the type of peg
for you in towers.sig (again, you should not modify this file) to be a
tuple containing a string and a stack. The string is meant to be the
peg's name or descriptor. Note that the stack closely matches the legal
move operation on a stack: discs can only be placed on or removed from
the top of a stack.
A move is a single step in the Hanoi puzzle, and consists of
taking a single disc from one peg and placing it onto another. We
define a move as a tuple of (disc, source peg, destination peg).
Each disc is represented by the integer number corresponding to its
size (see introduction). A disc with a higher number is larger than a
disc with a lower number, and hence higher number disc cannot be above
a lower number disc in a peg.
The source and destination pegs are represented by their string
names. The pegs are named "A", "B", and "C".
A solution to the Hanoi puzzle consists of an ordered
list of moves, that when applied to an initial configuration of all
discs in order on peg A, cause them to end up on peg B in the same
configuration as they were initially on peg A.
To make the types of functions in this structure easier
to read, we define "towers" to be a tuple of three pegs: A, B, and C,
with A being the starting peg and B being the final peg (C is the
auxiliary peg that will help you complete this task).
You will implement the following functions in towers-student.sml:
makePeg : string * int -> peg
Returns a new peg with the name, provided in the first
argument. This peg should have the first n discs already on it, where
n is specified as an argument.
isValid : peg -> bool
Indicates whether the given peg is in a valid configuration. We
define a valid configuration as one in which no disc is under a disc
with a larger size (i.e. for all i >= 1, stack(i-1) > stack(i)), where stack(k) denotes the kth element on the stack.
Note that a peg is not guaranteed to be in a consistent state. The underlying
stack that you implemented does not enforce this validity condition; the
condition is a property of this specific application of your stack. Therefore,
this function is necessary to ensure that your code is working with valid
stacks.
isLegalMove: disc * peg -> bool
Returns true if the specified disc can be placed on top of the
specified peg without creating an invalid configuration on the peg.
moveDisc : peg * peg -> peg * peg
Moves the top disc from the first peg onto the second peg (and
returns the resulting new pegs).
solve : towers -> towers * move list
This function, given an initial configuration specified in the input,
outputs a series of moves IN ORDER (i.e. the first element of
the list is the first move to be made) that will cause all discs
intially on the first peg to be moved onto the second peg. It should
also return the final configuration of pegs that would result from
applying the list of moves generated.
Here is some sample output that your program is expected to produce. In this case we have 3 discs on peg A initially and generate a move list that shows how to move them onto peg B:
- val a = makePeg("a", 3);
val a = ("a",[1,2,3]) : peg
- val b = makePeg("b", 0);
val b = ("b",[]) : peg
- val c = makePeg("c", 0);
val c = ("c",[]) : peg
- solve(a,b,c);
val it =
((("a",[]),("b",[1,2,3]),("c",[])),
[(1,"a","b"),(2,"a","c"),(1,"b","c"),(3,"a","b"),(1,"c","a"),(2,"c","b"),
(1,"a","b")]) : towers * move list
Be sure to test your Hanoi solver thoroughly using your own test cases in addition to the one we have provided.
Deterministic Finite Automata
In this problem we will concern ourselves with deterministic finite automata (DFAs). A DFA consists of the following elements:
- A set of states. For an automaton with n states, we will denote states with all numbers from 1 to n
- A start state
- A set of final (accepting) states
- A transition function (see below).
A
DFA is given an input string, which will be read one character at a
time. Our DFAs will read only strings consisting of characters #"a",
#"b". The empty string is a valid input to a DFA.
Whenever the DFA reads a character (and only then), the automaton moves from its current state p to a "next" state q. State q depends on both state p
and on the character read in input. The moves from one state to the
next as a result of reading an input character are described by the
transition function. Given any state and any character that can appear
in the input, the transition function specifies the next state. You can
assume that the transition function never returns an invalid state.
A DFA accepts an input string s
if and only if the automaton ends up in a final (accepting) state after
having started in the start state and after reading the entire input
string.
If the DFA starts in state s0 and reads in a string consisting of characters c0 c1 c2 . . . cn, then the sequence of the DFAs states will be s0 s1 s2 . . . sn. If there exist two integer numbers k and l such that 0 <= k < l <= n and sk = sl, we say that the input string lead to a loop (or cycle) in the sequence of states.
We implement DFAs using the following types:
datatype state = int
(* current state * input character * next state *)
type transition = state * char * state
(* current state * initial state * final states * transition function *)
type dfa = state * state * state list * transition list
Note that we don't explicitly represent the set of all states
(we can do this because we rely on the correctness of the transition
function to provide us with the correct "next" state at any time).
Here is an example of a DFA:
(2, 1, [2], [(1,#"a",1), (1,#"b",2), (2,#"b",2), (2,#"a",3), (3,#"a",3),
(3,#"b",3)])
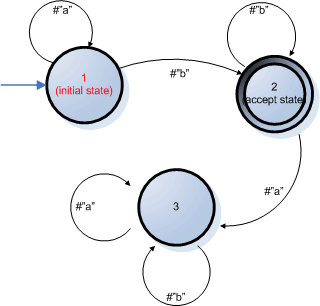
This
automaton is currently in state 2, its start state is state 1, and it
has a unique final state, 2. If the automaton is in state 1, then it
will stay there as long as the DFA sees only a 's in the input. The first b
character, if it occurs at all, will 'move' the automaton to state 2.
When in state 2, the DFA will stay there as long as it reads an
uninterrupted sequence of b 's. If an a occurs while
the automaton is in state 2, the DFA will reach state 3. State 3 is a
trap for this automaton - once there, the state does not change, not
matter what the input character is.
An interesting question is
that of the set of strings, if any, that a DFA accepts. If you study
the diagram above, you will realize that all strings consisting of an
unspecified number of a 's followed by at least one b will be accepted. For example, b, ab, bb, aaabbbbb will all be accepted, but a, abba, ababab will not be accepted.
Requirements
Complete the skeleton code in
dfa2.sml- Given a list of states l and a new state p, write a function that determines whether p is already in l or not. If p is already in l, the function returns l, otherwise p is prepended to l and the extended list is returned.
fun addNewState(states : state list, newstate : state) : state list = ...
- A transition function for a DFA should be complete,
i.e. it should define transitions for all possible combinations of
states and input characters. Assume that all states of the DFA appear
at least once in some position in the transition list.
fun isComplete(automaton: dfa): bool = ...
(* solve using fold, collect states that correspond to #"a" and #"b"
transitions into two lists, compare lists for completeness *)
- Given a string and a dfa, will the DFA accept the string? Also, what state does the automaton end up in?
fun testAccept(automaton: dfa, s: string): bool * state = ...
- Given a DFA and a string, will the string trigger a loop in the sequence of state transitions?
fun hasloop(automaton: dfa, s: string): bool = ...
It is possible to construct a DFA that
simulates the action of two DFAs in parallel. The standard construction
constructs a new state space from the Cartesian product (pair) of the
states of both DFAs. Let start, start' be the start states of both
DFAs. The start state of the composite automaton is START =
(start,start'), that is, the pair containing the start state of both
component DFAs.
We assume that any character read in by the
composite automaton is "seen" simultaneously by both component
automata. If the composite automaton is in state (p, q) and the current
input character would trigger transitions from p to r in the first
automaton, and from state q to t in the second automaton, then the
composite automaton will move from state (p, q) to state (r, t).
For this requirement, we would like you to simulate the action of this joint automaton, but not actually create it.
Write
the function that given two automata and an input string returns the list
of states composite automaton passes through until it complete reads in
the input string. List the states within the state tuple in the natural
order, i.e. the order in which the automata were specified, beginning with
the composite start state. Start the composite automaton
in its start state.
fun parallel(a0: dfa, a1: dfa, s: string): (state * state) list = ...
Problem 3: Fold on Binary Search Trees with BST abstract data type
We use the following datatype to represent a node in a binary search tree:
datatype 'a treenode = EMPTY | NODE of 'a treenode * 'a * 'a treenode
A binary search tree is a regular binary tree in which any node
n has the property that its associated key is strictly greater
than all of the keys associated with nodes in its left subtree, and it
is strictly smaller than any of the keys associated with nodes in its
right subtree. Equivalently, for each node n the node has the
property that its key is strictly greater than the key of its left
child (if such a child exists), and it is strictly smaller than the
key of its right child (if such a child exists).
Since our tree is parameterized, the notion of ordering will be
different depending for different underlying types 'a. For
this reason we represent a binary search tree as both a tree and an
ordering function for said tree:
type 'a bst = {root:'a treenode, compare:'a * 'a -> order}
In bst.sml we have provided a partial implementation of
binary search trees. It is your task to complete it. Further
specification of how each of the functions should behave is provided
in bst.sig. We have provided the following functions for
you:
(* Creates an empty binary search tree which uses given comparison function *)
val empty:('a * 'a -> order) -> 'a bst
(* evaluates to true if given binary search tree is empty *)
val isEmpty:'a bst -> bool
(* adds given element to given binary search tree.
* if said element already existed in said BST, returns it unchanged *)
val add:'a bst * 'a -> 'a bst
-
(* creates a binary search tree from a list and a comparison function *)
val fromList:'a list->('a * 'a -> order)->'a bst
1. The following BST operation has been left unimplemented. Please fill
in the body for it in bst.sml:
(* Checks if a tree is balanced. A tree is balanced if, for all nodes
|(# of nodes in left subtree) - (# of nodes in right subtree)| <= k *)
fun isBalanced({compare, root}:'a bst, k:int):bool
As you have seen, one extremely useful function when working with
lists is foldl and its dual foldr. In the following
we will extend the notion of 'folding' to binary search trees. Given
list l=[e1, e2, e3, ...,
ek] function foldl f a0 l is equivalent to
expression f(lk, ... f(l3, f(l2,
f(l1, a0)))). The equivalent expression for foldr is
f(l1, f(l2, f(l3,
... f(lk, a0))).
As opposed to lists, where we have two standard ways of examining each value
in sequence (left-to-right and right-to-left), in the case of binary trees we
have three systematic traversal orders. The following datatype declaration
captures this choice.
datatype traversal = PREORDER | INORDER | POSTORDER
- In pre-order traversal, first the node itself is visited, then the
left subtree, then the right subtree.
- In in-order traversal, first the left subtree is visited, then the
node itself, then the right subtree.
- In post-order traversal, first the left subtree is visited, then
the right subtree, then the node itself.
2. You will implement the function fold in bst.sml:
val fold:traversal -> ('a * 'b -> 'b) -> 'b -> 'a bst -> 'b
Given a BST t and its associated traversal (visiting order) o,
let us assume that the resulting enumeration of nodes is
n1, n2,
n3, ..., nk. Expression
fold o f a0 t
is equivalent to
f(nk, ... f(n3, f(n2, f(n1, a0)))).
The latter expression appears very similar to that for
foldl. Keep in mind, however, that the order of the nodes
depends on the traversal chosen.
3. Provide implementations for the functions below in
bst.sml. You must use the fold function as defined above
to implement the essential functionality in all your solutions. Try to
keep your functions short - almost all solutions are
one-liners. Provide solutions to this part even if your solution for
fold does not work - we will test these against our reference
implementation of fold.
(* evaluates to the number of elements in the given bst *)
val size:'a bst -> int
(* given a mapping function and a comparison function for the new type,
* maps a BST *)
val map:'a bst -> ('a -> 'b) -> ('b * 'b -> order) -> 'b bst (* creates a list ordered in ascending order
* containing all the values in the BST *)
val toList:'a bst -> 'a list
(* given two BSTs, creates a BST which is the union of their elements.
* Invariant: The ordering function of the two BSTs must be the same *)
val union:'a bst * 'a bst -> 'a bst
(* given two BSTs, creates a BST which is the intersection of their elements.
* Invariant: The ordering function of the two BSTs must be the same *)
val intersection:'a bst * 'a bst -> 'a bst
(* given a filtering function, returns a BST containing all the elements
* of original BST where the filter function returned true *)
val filter:('a -> bool) -> 'a bst -> 'a bst (* Creates a partition of the BST into the pair of BSTs (pos, neg) where
* pos contains all the elements of the original BST where the function
* returned true and neg contains all the elements of the original BST
* where the function returned false. *)
val partition:('a -> bool) -> 'a bst -> 'a bst * 'a bst
