Recitation 9: Proving running times

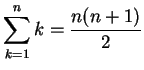
Note that we expect you to be familiar with mathematical induction. If you have not yet seen mathematical induction, you should review the handout discussing it and go to office hours if you have trouble.

The first thing we want to prove today is the equation:

$\displaystyle \sum_{k=1}^n k = \frac{n(n+1)}{2}$

The proof of this is in the induction examples handout. [Note to instructor: you should still show the proof on the board so the students can see the expected format of an induction proof]

Now that we have the basics down, we will use equations similar to the above frequently in our analysis of running times. Recall the formal definition of big-O:

$\displaystyle O(g(n)) = \{ f(n) \vert \exists c, n_0 . 0 \leq f(n) \leq c g(n) \quad \forall n \geq n_0 \}$

This definition is required when doing a formal proof of running times. Before we get to that, the first step is to write down the recurrence equations for your program. Actually getting the recurrence equations is not a trivial task -- the more complicated the program, the harder it is to figure out. At the basis of it is identifying the atomic operations of the program. This depends on the language you are using, etc. After identifying the atomic operations, you can combine them to determine the recursive calls and the constant values.

Insertion Sort Analysis

From experience and intuition, you know that insertion sort is O(n²), but now we want to prove it. Here is the code for insertion sort:

(* insert x into the appropriate position in ys *)
fun insert (cmp: ('a * 'a) -> order) (x:'a, xs:'a list) : 'a list =
  let fun loop(ys:'a list):'a list = 
    case ys of
      [] => [x]
    | y::rest => 
        (case cmp(x,y) of
           GREATER => y::(loop rest)
         | _ => x::ys)
  in 
    loop(xs)
  end


(* An insertion sort:  works by starting with an empty list and
 * successively inserts elements in their proper position.
 *)
fun insert_sort (cmp: 'a * 'a -> order) (xs: 'a list) : 'a list = 
    let (* Insert all elements of zs into ys --this could be done using fold
         * (see below).  
	 * Note that an invariant is that zs and ys contain all of the 
	 * elements in the original list xs.  (i.e., length(zs)+length(ys)=
	 * length(xs).*)
	fun insert_all (zs:'a list, ys:'a list): 'a list = 
	    (case zs of
		 [] => ys
	       | z::rest => insert_all(rest, insert cmp (z,ys)))
    in 
	(* insert all of xs into the empty list *)
	insert_all (xs, [])
    end

(* The above can be considerably simplified to just: *)
fun insert_sort2 (cmp: 'a * 'a -> order) : 'a list -> 'a list = 
  foldl (insert cmp) []

The recurrence equations for insertion sort are [Note to the instructor: derive them]:

T(1) = k₁
T(n) = T(n-1) + k₂n

Both k₁ and k₂ are constants. From our discussion of big-O in lecture, you know that an advantage of big-O is classifying programs by obscuring the constants. Since we don't know what k₁ or k₂ are, we can assume that they are both 1. If we did not assume that they are 1, we would simply have to scale the analysis accordingly later on. Leaving them as 1 just makes the whole thing a bit easier. That leaves us with the following recurrence equations for insertion sort:

T(1) = 1
T(n) = T(n−1) + n

There are two ways to come about deciding that insertion sort is O(n²): iterative method, and the guess and prove method. (Note other methods do exist, though they do not work for all cases.) First we will try to show insertion sort is O(n²) by the iterative method:

T(n) = T(n−1) + n
     = T(n−2) + n−1 + n
     = T(n−3) + n−2 + n−1 + n
     = T(n−4) + n−3 + n−2 + n−1 + n
     ...
     = T(2) + 3 + 4 + ... + n−4 + n−3 + n−2 + n−1 + n
     = T(1) + 2 + 3 + 4 + ... + n−4 + n−3 + n−2 + n−1 + n
     = 1 + 2 + 3 + 4 + ... + n−4 + n−3 + n−2 + n−1 + n

Basically, we keep substituting away until we notice a pattern in the iterations. From this we note:

$\displaystyle T(n) = \sum_{i=1}^n i \approx n^2$

So the running time is explicitly known to be n² with some constant factors involved. This matches the definition of O(n²).

The other method is to guess what the big-O set is for the running time and then prove it inductively using the formal definition. So, out of the blue, we're going to guess that the big-O running time of insertion sort is O(n²). Let's prove it!

First we choose constants c = 1 and n₀ = 1.
Property of n to prove

$\displaystyle 0 \leq T(n) \leq n^2$

Proof by Induction on n

Base Case: n = 1

T(n) = 1 = 1²

Induction Step:

Induction Hypothesis:
$\displaystyle 0 \leq T(n) \leq n^2$ for some $\displaystyle n \geq 1$
Property to prove for n+1:
$\displaystyle 0 \leq T(n+1) \leq (n+1)^2$

$\begin{displaymath} \begin{split} T(n+1) & = T(n) + n + 1 \\ & \leq n^2 + n +... ...thesis}}\\ & < n^2 + n + 1 + n \\ & = (n+1)^2 \end{split}\end{displaymath}$

The above proves the right-hand side of the equation. The left-hand side, 0 <= T(n+1), is obviously true.