In the last lecture we observed that the most important use of the "comment" feature of programming languages is to provide specifications of the behavior of declared functions, so that program modules can be used without inspecting their code (modular programming). The types (and names) of the functions implemented by a module are often useful hints to the behavior of these functions, but key aspects are often left out and must be provided in comment form. This is a lesson that applies to programming in many languages. For example, in Java, documenting the behavior of the public methods and classes is critical, because they form the externally visible interface once javadoc has extracted them. In C, functions defined in a source (".c") file should be described by comments in their corresponding header (".h") file.
So there is clearly a use for comments in interfaces (in SML: signatures). The topic of this lecture is the use of comments in module implementations (SML structures). The first question we must ask ourselves is who is going to read the comments written in module implementations. Because we are going to work hard to allow module users to program against the module while reading only its interface, clearly the module users are not the intended audience for such comments. Their purpose must be to clarify the implementation of the module for other implementers or maintainers of the same module. The best way to clarify the implementation is to write comments about the implementation that are intended to convince the reader that the implementation correctly implements the module interface.
For example, it would be inappropriate to copy the specifications of functions found in the module interface into the module implementation, because implementers can always look at the interface for the specification, and copying runs the risk of introducing inconsistency as the program evolves. Copying of code and specifications is a major source (if not the major source) of program bugs. This rule of thumb can be inconvenient to those using outdated editors that cannot view two files at a time, but the payoff is worth it.
The purpose of implementation comments is to explain details of the implementation that are not obvious to the reader. Thus, implementation comments are not always needed. For example, if we see the following structure and signature, it is obvious that the structure implements the signature and thus any additional comment in the structure would be superfluous:
signature CHOOSE = sig (* one_to_ten() is a number between one and ten, inclusive *) val one_to_ten: unit->int end structure Choose = struct fun one_to_ten() = 7 end
Implementation comments fall into two categories. The first category arises because a module implementation may define new types and functions that are purely internal to the module. If their significance is not obvious, these types and functions should be documented in much the same style that we have suggested for documenting interfaces. Often as the code is written it becomes apparent that the new types and functions defined in the module form an internal ADT. This is a warning sign of a likely opportunity for further modular abstraction: the internal ADT might be moved to a separate module and manipulated through its operations only.
The second category of implementation comments is associated with abstract data types; these comments are the focus of this lecture. Suppose we are implementing an ADT for a set of natural numbers. The interface might look something like this:
signature NATSET = sig (* a "set" is a set of natural numbers: e.g., {1,11,0}, {}, and {1001}*) type set (* empty is the empty set *) val empty : set (* single(x) is {x}. Requires: x >= 0 *) val single : int -> set (* union is set union. *) val union : set*set -> set (* contains(x,s) is whether x is a member of s *) val contains: int*set -> bool (* size(s) is the number of elements in s *) val size: set->int end
In a real signature for sets, we'd want map and fold
operations as well, but let's keep this simple. There are many ways to implement
this abstraction. One easy way is as a list of integers:
structure NatSet :> NATSET = struct type set = int list val empty = [] fun single(x) = [x] fun union(s1,s2) = s1@s2 fun contains(x,s) = case s of [] => false | h::t => x = h orelse contains(x,t) fun size(s) = case s of [] => 0 | h::t => size(t) + (if contains(h,t) then 0 else 1) end
This implementation has the advantage of simplicity although its performance
will be poor for large sets. Notice that I haven't bothered to write down the
types of the functions in the implementation. They aren't needed because they're
already present in the signature, so like the part of the specification that is
in the comments it doesn't need to be replicated in the struct. How do we know
whether the implementation satisfies the interface above? With the methodology
described so far, we need to carefully look at every method and all possible
interactions between the methods. Here is another implementation of NATSET.set
also using int list; this implementation is also correct (and also
slow). Notice that we are using the same representation type yet some important
aspects of the implementation are quite different. Again, it's a bit of
challenge to decide that this implementation really works without some kind of
comments.
structure NatSetNoDups :> NATSET = struct type set = int list val empty = [] fun single(x) = [x] fun contains(x,s) = case s of [] => false | h::t => x = h orelse contains(x,t) fun union(s1, s2) = foldl (fn (x,s) => if contains(x,s) then s else x::s) s1 s2 fun size(s) = length s end
Here's a third, completely different implementation with a fast contains
method. This implementation works pretty well as long as the integers stored in
the set are small. If they're not, it's a terrible implementation.
structure NatSetVec :> NATSET = struct type set = bool vector val empty:set = Vector.fromList [] fun single(x) = Vector.tabulate(x+1, fn(y) => x=y) fun union(s1,s2) = let val len1 = Vector.length(s1) val len2 = Vector.length(s2) fun merge(i) = (i < len1 andalso Vector.sub(s1, i)) orelse (i < len2 andalso Vector.sub(s2, i)) in Vector.tabulate(Int.max(len1, len2), merge) end fun contains(x,s) = x >= 0 andalso x < Vector.length(s) andalso Vector.sub(s,x) fun size(s) = Vector.foldl (fn (b,n) => if b then n+1 else n) 0 s end
There are ways to implement sets much better than any of these three, although they're a little more complicated. We'll see some of them in lectures coming up soon.
An important reason why we introduced the writing of function specifications
was to enable local reasoning: once a function has a spec, we can judge
whether the function does what it is supposed to without looking at the rest of
the program. We can also judge whether the rest of the program works without
looking at the code of the function. However, we cannot reason locally about the
individual functions in the three module implementations just given. The problem
is that we don't have enough information about the relationship between the
concrete types (e.g., int list, bool vector) and the
corresponding abstract type (set). This lack of information can be
addressed by adding two new kinds of comments to the implementation: the abstraction
function and the representation invariant for the abstract data type.
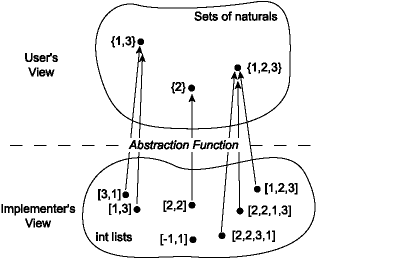
The user of one of the three NATSET ADT's should be unable to
tell them apart based on their behavior. As far as the user can tell, the values
of, say, NatSet.set act like the mathematical ideal of a set as
viewed through the operations. To the implementer, the lists [3,1],
[1,3], and [1,1,3] are distinguishable; to the user,
they both represent the abstract set {1,3} and cannot be told apart through the
operations of the NATSET signature. The user views the abstract
data type as containing a set of abstract values and associated operations; the
implementers knows that these abstract values are represented by concrete values
that may contain additional information invisible from the user's view. This
loss of information is described by the abstraction function, which is a
mapping from the concrete space of values to the abstract space. The abstraction
function for NatSet looks like this:

Notice that several concrete values may map to a single abstract value; that
is, the abstraction function may be many-to-one. It is also possible that
some concrete values, such as the list [-1,1], do not map to any
abstract value; the abstraction function may be partial. Using the
abstraction function, we can now talk about what it means for an implementation
of an abstraction to be correct. It is correct exactly when every
operation that takes place in the concrete space makes sense when mapped by the
abstraction function into the abstract space. This can be visualized as a commutation
diagram:
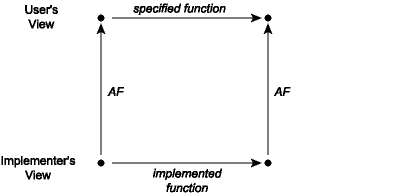
A commutation diagram means that if we take the two paths around the diagram, we have to get to the same place. Suppose that we start from a concrete value and apply the actual implementation of some ADT operation to it. When viewed abstractly, the result of the implementation should be a value that is a possible result of applying the function as described in its specification to the abstract view of the actual inputs. For example, consider the union function applied to the concrete pair ([1,3],[2,2]), which would be the lower-left corner of the diagram. The result of this operation is the list [2,2,1,3], whose corresponding abstract value is the list {1,2,3}. Note that if we apply the abstraction function AF to the lists [1,3] and [2,2], we have the sets {1,3} and {2}. The commutation diagram requires that in this instance the union of {1,3} and {2} is {1,2,3}, which is of course true.
Some specifications, as we have seen, are nondeterministic: they do not fully specify the abstract behavior of the functions. For nondeterministic specifications there are several possible arrows leading from the abstract state at the upper left corner of the commutation diagram to other states. The commutation diagram is satisfied as long as the implemented function completes the diagram for one of those arrows.
The abstraction function is important for deciding whether an implementation
is correct, and therefore it belongs as a comment in the implementation of any
abstract data type. For example, in the NatSet structure, we could
document the abstraction function as follows:
structure NatSet :> NATSET = struct type set = int list (* Abstraction function: the list [a1,...,an] represents the smallest set * containing all of a1,...,an. The list may contain duplicates. * The empty list represents the empty set. *) val empty = [] ...
This comment explicitly points out that the list may contain duplicates,
which is probably helpful as a reinforcement of the first sentence. Similarly,
the case of an empty list is mentioned explicitly for clarity. When we look at
the abstraction function for NatSetNoDups, there is a hint of an
important difference: we can write the abstraction function a bit more simply
because we know that the elements are distinct:
structure NatSetNoDups :> NATSET = struct type set = int list (* Abstraction function: the list [a1,...,an] represents the set * {a1,...,an}. The empty list represents the empty set. *) val empty = [] ...We could also stick with the same abstraction function that we wrote for NatSet, because when applied to lists containing distinct integers, that abstraction function gives the same result as this one.
Finally, we can document the abstraction function of NatSetVec:
structure NatSetVec :> NATSET = struct type set = bool vector (* Abstraction function: the vector v represents the set of all natural numbers i such that sub(v,i) = true *) val empty:set = Vector.fromList [] ...
Another option for defining the abstraction function is to give pseudo-code
defining it; for example, in the case of NatSet we might write:
(* Abstraction Function:AF([]) = {} AF(h::t) = {h} U AF(t) (where "U" is mathematical set union)*)
However, using English is generally recommended because of the potential for confusion when the notation of the implementation (SML code) meets the notation of the abstract domain (mathematics, in this case).
In practice the words "Abstraction function" are usually omitted when practitioners write code. However, we will ask you to do it because it's a useful reminder that that is what you are writing in a comment like the ones above. Whenever you write code to implement what amounts to an abstract data type, you should write down the abstraction function explicitly, and certainly keep it in mind.
We observed above that the abstraction function may be a partial function. In
fact, in the case of NatSet and NatSetNoDups, the
abstraction function is partial because it maps lists containing negative
integers (such as [-1,1]) to sets that are not part of the space of
abstract values. In order to make sure that an implementation works—that it
completes the commutation diagram—it had better be the case that the
implementation never produces any concrete values that do not map to abstract
values.
There is a corresponding problem on the input side. Suppose that in writing NatSetNoDups
we used the same abstraction function as for NatSet—which we
argued above is fine because that abstraction function gives exactly the same
result on all lists that the module implementation will ever produce:
(* Abstraction function: the list [a1,...,an] represents the smallest set
containing all of a1,...,an. The list may contain duplicates. The empty
list represents the empty set.
This abstraction function isn't enough to convince us that the implementation
is correct. A list like [2,2]is mapped by the abstraction function
to the valid abstract value {2}, but it doesn't satisfy the commutation diagram
because size([2,2]) = 2 yet the size of AF([2,2]) =
{2} is 1. (The abstract and concrete views of integers are essentially the
same.) In general, we need to restrict the domain of the abstraction
function to those values on which the implementation is going to work properly.
The concrete type (int list) is an imprecise characterization of the domain; we
need to provide a more precise characterization that we cannot expect SML to
understand. This is the representation invariant (or just rep
invariant).
Representation invariant: given the rep [a_1,...,a_n], all elements are
nonnegative, and no two elements are equal. The rep [] is also valid. *)
This condition identifies a subset of the space of values of the type used for concrete representations. The idea is that all of the values produced by the implementation will satisfy the representation invariant, and that the abstraction function is defined on all values that satisfy the rep invariant. Therefore the implementation is guaranteed to produce valid concrete values. Because the rep invariant and the abstraction function are so closely linked, they are documented together in the module implementation. The relationship between the representation invariant and the abstraction function is depicted in this figure:
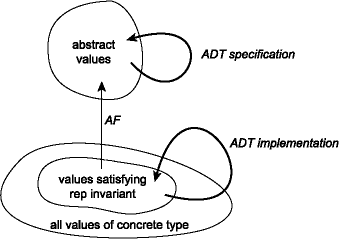
The rep invariant is a condition that is intended to hold for all values of the abstract type (e.g., set). Therefore, in implementing one of the operations of the abstract data type, it can be assuming that any arguments of the abstract type satisfy the rep invariant. This assumption restores local reasoning about correctness, because we can use the rep invariant and abstraction function to judge whether the implementation of a single ADT operation is correct in isolation from the rest of the module. It is correct if, assuming that:
we can show that
The rep invariant makes it easier to write code that is provably correct,
because it means that we don't have to write code that works for all possible
incoming concrete representations--only those that satisfy the rep invariant.
This is why NatSetNoDups.union doesn't have to work on lists that
contain duplicate elements. On return there is a corresponding responsibility to
produce only values that satisfy the rep invariant. As suggested in the figure
above, the rep invariant holds for all reps both before and after the functions,
which is why we call it an invariant at all.
Rep invariants are useful even when writing modules that are not easily considered to be providing abstract data types. Sometimes it is difficult to identify an abstract view of data that is provided by the module; the abstraction function can be expressed only approximately. The rep invariant is important even without an abstraction function, because it documents the possible representations that the code is expected to handle correctly. This is useful in understanding how the code works, and also in maintenance, because the maintainer can avoid changes to the code that violate the invariant.
Let us consider the rep invariant for the vector implementation of NATSET.
There is some question about what we should write. One possibility is to write
the strongest possible specification of the possible values that can be created
by the implementation. It happens that the vector representing the set never has
trailing false values:
structure NatSetVec :> NATSET = struct type set = bool vector (* Abstraction function: the vector v represents the set of all natural numbers i such that sub(v,i) = true Representation invariant: the last element of v is true *) val empty:set = Vector.fromList []
This representation invariant describes an interesting property of the
implementation that may be useful in judging its performance. However, we don't
need this rep invariant in order to show that the implementation is correct. If
there were no rep invariant, we could still argue that the implementation works
properly. All of the operations of NatSetVec will work even if sets
are somehow introduced that violate the no-trailing-false property. It is not
necessary to have the rep invariant in order to argue that the operations of NatSetVec
are correct according to the 4-point plan above.
Further, a strong rep invariant is not always the best choice, because it restricts future changes to the module. We described interface specifications as a contract between the implementer of a module and the user. A rep invariant is a contract between the implementer and herself, or among the various implementers of the module, present and future. According to assumption 2, above, ADT operations may be implemented assuming that the rep invariant holds. If the rep invariant is ever weakened (made more permissive), some parts of the implementation may break.Thus, one of the most important purposes of the rep invariant is to document exactly what may and what may not be safely changed about a module implementation. A weak rep invariant forces the implementer to work harder to produce a correct implementation, because less can be assumed about concrete representation values, but conversely it gives maximum flexibility for future changes to the code.