Suppose we want a data structure to implement either a mutable set of elements (with operations like contains, add, and remove that take an element as an argument) or a mutable map from keys to values (with operations like get, put, and remove that take a key for an arguments). A mutable map is also known as an associative array. We've now seen a few data structures that could be used for both of these implementation tasks.
We consider the problem of implementing sets and maps together because most data structures that can implement a set can also implement a map. A set of key–value pairs can act as a map, as long as the way we compare key–value pairs is to compare the keys. Alternatively, we can view the transformation from a set to a map as starting with a data structure that implements set of keys and then adding an associated value to each data structure node that stores a key.
Here are the data structures we've seen so far, with the asymptotic complexities for each of their key operations:
| Data structure | lookup (contains/get) | add/put | remove |
|---|---|---|---|
| Array | O(n) | O(1) | O(n) |
| Function | O(1) | O(n) | N/A |
| Linked list | O(n) | O(1) | O(n) |
| Search tree | O(lg n) | O(lg n) | O(lg n) |
Naturally, we might wonder if there is a data structure that can do better. And it turns out that there is: the hash table, one of the best and most useful data structures there is—when used correctly.
Many variations on hash tables have been developed. We'll explore the most common ones, building up in steps.
While arrays make a slow data structure when you don't know what index to look at, all of their operations are very fast when you do. This is the insight behind the direct address table. Suppose that for each element that we want to store in the data structure, we can determine a unique integer index in the range 0..m–1. That is, we need an injective function that maps elements (or keys) to integers in the range. Then we can use the indices produced by the function to decide at which index to store the elements in an array of size m.
For example, suppose we are maintaining a collection of objects representing houses on the same street. We can use the street address as the index into a direct address table. Not every possible street address will be used, so some array entries will be empty. This is not a problem as long as there are not too many empty entries. However, it is often hard to come up with an injective function that does not require many empty entries. For example, suppose that instead we are maintaining a collection of employees whom we want to look up by social security number. Using the social security number as the index into a direct address table means we need an array of 10 billion elements, almost all of which are likely to be unused. Even assuming our computer has enough memory to store such a sparse array, it will be a waste of memory. Furthermore, on most computer hardware, the use of caches means that accesses to large arrays are actually significantly slower than accesses to small arrays—sometimes, two orders of magnitude slower!
Instead of requiring that the key be mapped to an index without any collisions,
we allow collisions in which two keys maps to the same array index. To avoid
having many collisions, this mapping is performed by a hash function
that maps the key in a reproducible but “random” way to a hash that
is a legal array index. If the hash function is good, collisions occur as if
completely at random. Suppose that we are using an array with 13 entries and
our keys are social security numbers, expressed as long values.
Then we might use modular hashing, in which the array index is computed
as key % 13. This is not a very random hash function, but is
likely to be good enough unless there is an adversary purposely trying to produce
collisions.
There are two main ideas for how to deal with collisions. The best way is usually chaining: each array entry corresponds to a bucket containing a mutable set of elements. (Confusingly, this approach is also known as closed addressing or open hashing.) Typically, the bucket is implemented as a linked list, so each array entry (if nonempty) contains a pointer to the head of the linked list.
To check whether an element is in the hash table, the key is first hashed to find the correct bucket to look in. Then, the linked list is scanned to see if the desired element is present. If the linked list is short, this scan is very quick.
An element is added or removed by hashing it to find the correct bucket. Then, the bucket is checked to see if the element is there, and finally the element is added or removed appropriately from the bucket in the usual way for linked lists.
Another approach to collision resolution that is worth knowing about is probing. (Confusingly, this technique is also known as open addressing or closed hashing.) Rather than put colliding elements in a linked list, all elements are stored in the array itself. When adding a new element to the hash table creates a collision, the hash table finds somewhere else in the array to put it. The simple way to find an empty index is to search ahead through the array indices with a fixed stride (often 1), looking for an unused entry; this linear probing strategy tends to produce a lot of clustering of elements in the table, leading to bad performance. A better strategy is to use a second hash function to compute the probing interval; this strategy is called double hashing. Regardless of how probing is implemented, however, the time required to search for or add an element grows rapidly as the hash table fills up. By contrast, the performance of chaining degrades more gracefully, and chaining is usually faster than probing even when the hash table is not nearly full. Therefore chaining is usually preferred over probing.
A recently popular variant of closed hashing is Cuckoo hashing, in which two hash functions are used. Each element is stored at one of the two locations computed by these hash functions, so at most two table locations must be consulted in order to determine whether the element is present. If both possible locations are occupied, the newly added element displaces the element that was there, and this element is then re-added to the table. In general, a chain of displacements occurs.
Suppose we are using a chained hash table with m buckets, and the number of elements in the hash table is n. Then the average number of elements per bucket is n/m, which is called the load factor of the hash table, denoted α. When an element that is not in the hash table is searched for, the expected length of the linked list traversed is α. Since there is always the initial (constant) cost of hashing, the cost of hash table operations with a good hash function is, on average, O(1 + α). If we can ensure that the load factor α never exceeds some fixed value αmax, then all operations will be O(1 + αmax) = O(1).
In practice, we will get the best performance out of hash tables when α is within a narrow range, from approximately 1/2 to 2. If α is less than 1/2, the bucket array is becoming sparse and a smaller array is likely to give better performance. If α is greater than 2, the cost of traversing the linked lists limits performance.
One way to hit the desired range for α is to allocate the bucket array is just the right size for the number of elements that are being added to it. In general, however, it's hard to know ahead of time what this size will be, and in any case, the number of elements in the hash table may need to change over time.
Since we can't predict how big to make the bucket array ahead of time, why not dynamically adjust its size? We can use a resizable array data structure to achieve this. Instead of representing the hash table as a bucket array, we introduce a header object that contains a pointer to the current bucket array, and also keeps track of the number of elements in the hash table.
Whenever adding an element would cause α to exceed αmax, the hash table generates a new bucket array whose size is a multiple of the original size. Typically, the new bucket array is twice the size of the current one. Then, all of the elements must be rehashed into the new bucket array. This means a change of hash function; typically, hash functions are designed so they take the array size m as a parameter, so this parameter just needs to be changed.
Since some add() operations cause all the elements to be rehashed, the cost of each such operation is O(n) in the number of elements. For a large hash table, this may take enough time that it causes problems for the program. Perhaps surprisingly, however, the cost per operation is still always O(1). In particular, any sequence of n operations on the hash table always takes O(n) time, or O(1) per operation. Therefore we say that the amortized asymptotic complexity of hash table operations is O(1).
To see why this is true, consider a hash table with αmax = 1. The most expensive sequence of n operations we can do is a series of n add() calls where n = 2j, meaning that the hash table resizes on the very last call to add(). The cost of the operations can be measured in the number of uses of the hash functions. There are n initial hashes when elements are added. The hash table is resized whenever it hits a power of two is size, so the extra hashes caused by resizing are 1 + 2 + 4 + 8 + ... + 2j. This sum is bounded by 2*2j = 2n, so the total number of hashes is less than 3n, which is O(n).
Notice that it is crucial that the array size grows geometrically (doubling). It may be tempting to grow the array by a fixed increment (e.g., 100 elements at time), but this causes n elements to be rehashed O(n) times on average, resulting in O(n2) total insertion time, or amortized complexity of O(n).
Hash tables are one of the most useful data structures ever invented. Unfortunately, they are also one of the most misused. Code built using hash tables often falls far short of achievable performance. There are two reasons for this:
Clearly, a bad hash function can destroy our attempts at a constant running time. A lot of obvious hash function choices are bad. For example, if we're mapping names to phone numbers, then hashing each name to its length would be a very poor function, as would a hash function that used only the first name, or only the last name. We want our hash function to use all of the information in the key. This is a bit of an art. While hash tables are extremely effective when used well, all too often poor hash functions are used that sabotage performance.
Recall that hash tables work well when the hash function satisfies the simple uniform hashing assumption -- that the hash function should look random. If it is to look random, this means that any change to a key, even a small one, should change the bucket index in an apparently random way. If we imagine writing the bucket index as a binary number, a small change to the key should randomly flip the bits in the bucket index. This is called information diffusion. For example, a one-bit change to the key should cause every bit in the index to flip with 1/2 probability.
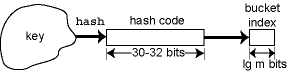
As we've described it, the hash function is a single function that maps from the key type to a bucket index. In practice, the hash function is the composition of two functions, one provided by the client and one by the implementer. This is because the implementer doesn't understand the element type, the client doesn't know how many buckets there are, and the implementer probably doesn't trust the client to achieve diffusion.
The client function hclient first converts the key into an integer hash code, and the implementation function himpl converts the hash code into a bucket index. The actual hash function is the composition of these two functions, hclient∘himpl:

To see what goes wrong, suppose our hash code function on objects is the memory address of the objects, as in Java. This is the usual choice. And suppose that our implementation hash function is like the one in SML/NJ; it takes the hash code modulo the number of buckets, where the number of buckets is always a power of two. This is also the usual implementation-side choice. But memory addresses are typically equal to zero modulo 16, so at most 1/16 of the buckets will be used, and the performance of the hash table will be 16 times slower than one might expect.
When the distribution of keys into buckets is not random, we say that the hash table exhibits clustering. It's a good idea to test your function to make sure it does not exhibit clustering with the data. With any hash function, it is possible to generate data that cause it to behave poorly, but a good hash function will make this unlikely.
A good way to determine whether your hash function is working well is to measure clustering. If bucket i contains xi elements, then a good measure of clustering is the following:
A uniform hash function produces clustering C near 1.0 with high probability. A clustering measure of C > 1 greater than one means that the performance of the hash table is slowed down by clustering by approximately a factor of C. For example, if m=n and all elements are hashed into one bucket, the clustering measure evaluates to n. If the hash function is perfect and every element lands in its own bucket, the clustering measure will be 0. If the clustering measure is less than 1.0, the hash function is spreading elements out more evenly than a random hash function would; not something to count on!
Unfortunately most hash table implementations do not give the client a way to measure clustering. This means the client can't directly tell whether the hash function is performing well or not. Hash table designers should provide some clustering estimation as part of the interface. Note that it's not necessary to compute the sum of squares of all bucket lengths; picking a few at random is cheaper and usually good enough.
The reason the clustering measure works is because it is based on an estimate of the variance of the distribution of bucket sizes. If clustering is occurring, some buckets will have more elements than they should, and some will have fewer. So there will be a wider range of bucket sizes than one would expect from a random hash function.
For those who have taken some probability theory: Consider bucket i containing xi elements. For each of the n elements, we can imagine a random variable ej, whose value is 1 if the element lands in bucket i (with probability 1/m), and 0 otherwise. The bucket size xi is a random variable that is the sum of all these random variables:
xi = ∑j∈1..n ejLet's write ⟨x⟩ for the expected value of variable x, and Var(x) for the variance of x, which is equal to ⟨(x - ⟨x⟩)2⟩ = ⟨x2⟩ - ⟨x⟩2. Then we have:
⟨ej⟩ = 1/m
⟨ej2⟩ = 1/m
Var(ej) = 1/m - 1/m2
⟨xi⟩ = n⟨ej⟩ = α
The variance of the sum of independent random variables is the sum of their variances. If we assume that the ej are independent random variables, then:
Var(xi) = n Var(ej) = α - α/m = ⟨xi2⟩ - ⟨xi⟩2
⟨xi2⟩ = Var(xi) + ⟨xi⟩2
= α(1 - 1/m) + α2
Now, if we sum up all m of the variables xi, and divide by n, as in the formula, we should effectively divide this by α:
(1/n) ⟨∑ xi2⟩ = (1/α)⟨xi2⟩ = 1 - 1/m + αSubtracting 1, we get (n−1)/m. The clustering measure multiplies this by its reciprocal to get 1.
Suppose instead we had a hash function that hit only one of every c buckets, but was random among those buckets. In this case, for the non-empty buckets, we'd have
⟨ej⟩ = ⟨ej2⟩ = c/m
⟨xi⟩ = αc
(1/n) ⟨∑ xi2⟩ - 1 = αc − c/m
= c(n-1)/mTherefore, the clustering measure evaluates in this case to c. In other words, if the clustering measure gives a value significantly greater than one, it is like having a hash function that doesn't hit a substantial fraction of buckets.
For a hash table to work well, we want the hash function to have two properties:
As a hash table designer, you need to figure out which of the client hash function and the implementation hash function is going to provide diffusion. For example, Java hash tables provide (somewhat weak) information diffusion, allowing the client hashcode computation to just aim for the injection property. In SML/NJ hash tables, the implementation provide only the injection property. Regardless, the hash table specification should say whether the client is expected to provide a hash code with good diffusion (unfortunately, few do).
If clients are sufficiently savvy, it makes sense to push the diffusion onto them, leaving the hash table implementation as simple and fast as possible. The easy way to accomplish this is to break the computation of the bucket index into three steps.
There are several different good ways to implement diffusion (step 2): multiplicative hashing, modular hashing, cyclic redundancy checks, and secure hash functions such as MD5 and SHA-1. They offer a tradeoff between collision resistance and performance.
Usually, hash tables are designed in a way that doesn't let the client fully control the hash function. Instead, the client is expected to implement steps 1 and 2 to produce an integer hash code, as in Java. The implementation side then uses the hash code and the value of m (usually not exposed to the client, unfortunately) to compute the bucket index.
Some hash table implementations expect the hash code to look completely random, because they directly use the low-order bits of the hash code as a bucket index, throwing away the information in the high-order bits. Other hash table implementations take a hash code and put it through an additional step of applying an integer hash function that provides additional diffusion. With these implementations, the client doesn't have to be as careful to produce a good hash code,
Any hash table interface should specify whether the hash function is expected to look random. If the client can't tell from the interface whether this is the case, the safest thing is to compute a high-quality hash code by hashing into the space of all integers. This may duplicate work done on the implementation side, but it's better than having a lot of collisions.
With modular hashing, the hash function is simply h(k) = k mod m for some m (usually, the number of buckets). The value k is an integer hash code generated from the key. If m is a power of two (i.e., m=2p), then h(k) is just the p lowest-order bits of k. The SML/NJ implementation of hash tables does modular hashing with m equal to a power of two. This is very fast but the the client needs to design the hash function carefully.
The Java Hashmap class is a little friendlier but
also slower: it uses modular hashing with m
equal to a prime number. Modulo operations can be accelerated by
precomputing 1/m as a fixed-point number, e.g. (231/m). A precomputed table
of various primes and their fixed-point reciprocals is therefore
useful with this approach, because the implementation can then use
multiplication instead of division to implement the mod operation.
A faster but often misused alternative is multiplicative hashing, in which the hash index is computed as ⌊m * frac(ka)⌋. Here k is again an integer hash code, a is a real number and frac is the function that returns the fractional part of a real number. Multiplicative hashing sets the hash index from the fractional part of multiplying k by a large real number. It's faster if this computation is done using fixed point rather than floating point, which is accomplished by computing (ka/2q) mod m for appropriately chosen integer values of a, m, and q. So q determines the number of bits of precision in the fractional part of a.
Here is an example of multiplicative hashing code, written assuming a word size of 32 bits:
val multiplier: Word.word = 0wx678DDE6F (* a recommendation by Knuth *)
fun findBucket({arr, nelem}, e) (f:bucket array*int*bucket*elem->'a) =
let
val n = Word.fromInt(Array.length(arr))
val d = (0wxFFFFFFF div n)+0w1
val i = Word.toInt(Word.fromInt(Hash.hash(e)) * multiplier div d)
val b = Array.sub(arr, i)
in
f(arr, i, b, e)
end
Multiplicative hashing works well for the same reason that linear congruential multipliers generate apparently random numbers—it's like generating a pseudo-random number with the hashcode as the seed. The multiplier a should be large and its binary representation should be a "random" mix of 1's and 0's. Multiplicative hashing is cheaper than modular hashing because multiplication is usually considerably faster than division (or mod). It also works well with a bucket array of size m=2p, which is convenient.
In the fixed-point version, The division by 2q is crucial. The common mistake when doing multiplicative hashing is to forget to do it, and in fact you can find web pages highly ranked by Google that explain multiplicative hashing without this step. Without this division, there is little point to multiplying by a, because ka mod m = (k mod m) * (a mod m) mod m . This is no better than modular hashing with a modulus of m, and quite possibly worse.
For a longer stream of serialized key data, a cyclic redundancy check (CRC) makes a good, reasonably fast hash function. A CRC of a data stream is the remainder after performing a long division of the data (treated as a large binary number), but using exclusive or instead of subtraction at each long division step. This corresponds to computing a remainder in the field of polynomials with binary coefficients. CRCs can be computed very quickly in specialized hardware. Fast software CRC algorithms rely on precomputed tables of data. As a rule of thumb, CRCs are about 3-4 times slower than multiplicative hashing.
Sometimes software systems are used by adversaries who might try to pick keys that collide in the hash function, thereby making the system have poor performance. Cryptographic hash functions are hash functions that try to make it computationally infeasible to invert them: if you know h(x), there is no way to compute x that is asymptotically faster than just trying all possible values and see which one hashes to the right result. Usually these functions also try to make it hard to find different values of x that cause collisions; they are collision-resistant. Examples of cryptographic hash functions are MD5 and SHA-1. MD5 is not as strong as once thought, but it is roughly four times faster than SHA-1 and usually still fine for generating hash table indices. As a rule of thumb, MD5 is about twice as slow as using a CRC.
High-quality hash functions can be expensive. If the same values are being hashed repeatedly, one trick is to precompute their hash codes and store them with the value. Hash tables can also store the full hash codes of values, which makes scanning down one bucket fast. In fact, if the hash code is long and the hash function is high-quality (e.g., 64+ bits of a properly constructed MD5 digest), two keys with the same hash code are almost certainly the same value. Your computer is then more likely to get a wrong answer from a cosmic ray hitting it than from a hash code collision.
This lecture borrows from material developed by Prof. Andrew Myers originally for CS 3110 but now used in CS 2112.