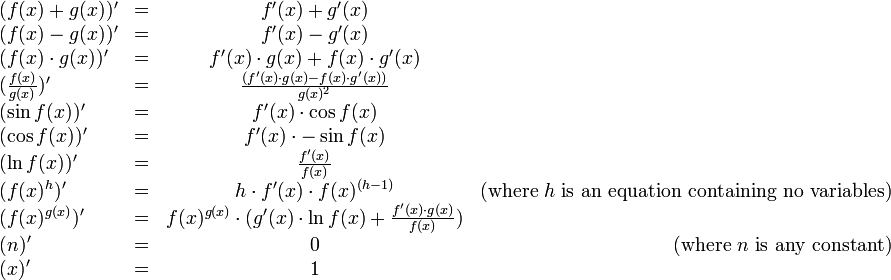Problem Set 2: Folding, Diff, and Symbolic Differentiation

Due Thursday, February 14, 23:59

• Version 2: Added part 3, changed commas in part 2 examples to semicolons Version 3: Added part 3, changed commas in part 2 examples to semicolons

Instructions

This problem set has three parts. You should write your solution to each part in a separate file: warmup.ml, diff.ml, and expression.ml. To help get you started, we have provided a stub file for each part on CMS. You should download and edit these files. Once you have finished, submit your solution using CMS, linked from the course website.

Note: Unless otherwise mentioned, you may not use the rec keyword in this problem set. You may find the standard List module functions, namely fold_left, particularly useful. You should consider making your solution tail-recursive, as points will be taken off if your function stack-overflows with large input. Points will also be deducted for abuse of the @ operator. Side effects are not allowed.

Important notes about grading:

1. Compile errors: All code you submit must compile. Programs that do not compile will likely receive an automatic zero. If you are having trouble getting your assignment to compile, please visit consulting hours. If you run out of time, it is better to comment out the parts that do not compile, than hand in a more complete file that does not compile.
2. Naming: We will be using an automatic grading script, so it is crucial that you name your functions and order their arguments according to the problem set instructions, and that you place the functions in the correct files. Otherwise you may not receive credit for a properly written function.
3. Code style: Finally, please pay attention to style. Refer to the CS 3110 style guide and lecture notes. Ugly code that is functionally correct may still lose points. Take the extra time to think out the problems and find the most elegant solutions before coding them up.
4. Late assignments: Please carefully review the course website's policy on late assignments, as all assignments handed in after the deadline will be considered late. Verify on CMS that you have submitted the correct version, before the deadline. Submitting the incorrect version before the deadline and realizing that you have done so after the deadline will be counted as a late submission.

Part 1: Warm-Up to Folding (10 pts)

1. Write a function simple_stats : float list -> float * float * float * float * int
   Given a float list, return a tuple of (min, max, mean, range, number of elements) from the input (range is the difference between the min and the max). For full credit, you must use only one list folding function, and all of the work must be done inside of this function. Note: You may raise a suitable exception if the list is empty.

Part 2: Diff (45 pts)

1. Write a function prepend_all : 'a list list -> 'a -> 'a list list that takes in a list of lists of any type and an element of that type and returns all of the lists with that element added to the front of the list. For example:

   prepend_all [[2; 4; 5]; []; [3; 10]] 1 =
     [1; 2; 4; 5]; [1]; [1; 3; 10]]

2. Write a function union_lists : 'a list -> 'a list -> 'a list that takes in two lists of the same type and returns a list which contains the union of the elements of the two lists (i.e. there should be no duplicates in the list returned) You may assume that the argument lists are already valid sets.
3. Write a function lcs : 'a list -> 'a list -> 'a list list that takes two lists and computes the longest common subsequence (LCS) of the elements in the two lists. This function should return a list of lists, and which contains all possible LCS in case of a tie. Note that a subsequence is not the same as a substring. If a sequence has some of its elements removed without the order of the remaining ones changed, then the resulting sequence is a subsequence of the original sequence. For example, [A; C] is a subsequence of [A; B; C; D]. The LCS of two lists is then the longest subsequence that is in both lists. The general algorithm for doing computing the LCS is described below.
   
   Consider two nonempty lists, lst₁ and lst₂. Let fin₁ be the last element in lst₁ and start₁ be the rest of lst₁, and fin₂ and start₂ be the same for lst₂. Say that we want to find the LCS of lst₁ and lst₂. If fin₁ = fin₂, then this element must be in subsequence, and the rest of the subsequence can be found by recursing on start₁ and start₂. If fin₁ <> fin₂, then they cannot both be in the LCS. Therefore, we take the best out of three cases:
   1. fin₁ is not in the subsequence, so we can find the subsequence by recursing on start₁ and lst₂ and take the longest subsequence of the two
   2. fin₂ is not in the subsequence, so we can find the subsequence by recursing on lst₁ and start₂ and take the longest subsequence of the two
   3. Neither fin₁ nor fin₂ is in the subsequence, so we can find the subsequence by recursing on start₁ and start₂ and take the longest subsequence of the two
   The recursive algorithm described above will work, but it will be extremely slow because it runs in exponential time, and will end up repeating work a very large number of times.
   
   To fix this problem, we are going to use a technique called dynamic programming, and incrementally build up to the solution starting from the base case of finding the LCS of two empty lists.
   
   In the picture below, the list [G; A; C] is lined up against the first column, and the list [A; G; C; A; T] is lined up across the first row. In this matrix, finding the value at position (row, column) is the same as finding the LCS between the lists represented by that column and that row. For example, if we label the cell at the intersection of the two empty lists as (0, 0), then cell (2, 3) represents the LCS of [G; A] and [A; G; C]. This means that if we can fill the bottom right corner of the matrix, then we have found the LCS of [G; A; C] and [A; G; C; A; T].
   
   

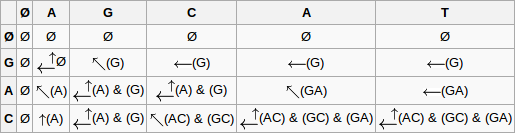   Figure 1 Image from Wikipedia

   
   Say we want to fill in cell (2, 4). Since fin₁ = fin₂, we simply take the result in (1, 3) and add A to all of them.
   
   Suppose instead that we are trying to fill in cell (2, 3). We can see that A and C are not the same. This is the fin₁ <> fin₂ case, and we use the best of the three cases listed above. The result of start₁ and lst₂ is in the cell at (1, 3). The result of lst₁ and start₂ is in the cell at (2, 2). The result of start₁ and start₂ will be included in one of those two cells already, so we do not have to worry about it. We have two cases when comparing results:
   1. If the length of LCS in one cell is longer than the length of LCS in the other cell, then we use the result from the first cell
   2. If the length of LCS in both cells is equal, then we take the union of the results
   We can run this algorithm by filling in the matrix starting from the top left and going across each row. Notice how it is not necessary to store the entire matrix. Since each row only depends on the row before, it is enough to keep track of only the previous row and the row that you are currently building.
   
   If you would like to read more about the longest common subsequence, you can check out Wikipedia. Example output to the problem shown in the table is given below. Note that the order in which you give the best subsequences does not matter.

   lcs [A; G; C; A; T] [G; A; C] = [[A; C]; [G; C]; [G; A]]

4. You may use the rec keyword for this problem.
   Write a function diff : string -> string -> string list that takes the names of two files as strings and returns a list of strings representing the changes between the two files. The first file should be the original file, and the second should be the updated version. After loading the two files using the provided function, you can use the result from your lcs to produce the output (you may choose any of the subsequences in case of a tie). The output should be computed as follows:
   1. Any line that appears in both the original file and the LCS or in both the updated file and the LCS is unchanged, and should have no effect on the output.
   2. Any line that is in the original file but not in the LCS must have been deleted. Deletions from the original file should start with "- " prepended to the beginning of the line.
   3. Any line that is in the updated file but not in the LCS must have been added. Additions to the updated file should start with "+ " prepended to the beginning of the line.
   4. A change should be represented as a deletion and then an addition. If multiple lines are changed, all of the deletions should appear before all of the additions.
   The relative ordering of lines must be consistent in the output. However, you can treat changes to multiple lines as deleted first then added second. The figure below shows an example of how the function works:

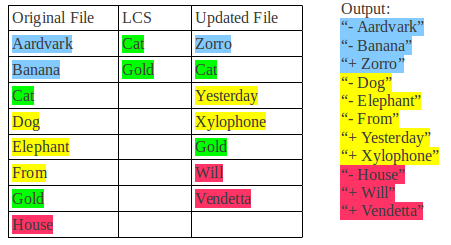   Figure 2: A diff Example

   
   Each non-green color group represents a "change", and the output always shows the deletion first and addition second.
   
   As you test your code, you may come across cases where the diff produces a valid output, but it could have been cleaner. For example, you can run your diff on these two inputs

   programming          programming
   language             using
   ocaml                programming
   is                   language
   awesome!             ocaml
                        is
                        awesome!

   and get this output:

   	"+ using"
   	"+ programming"

   This is a bit bothersome, as it is clear that the first two lines in the new file are the ones that were added, not the second and third. We are not concerned about this, but there are some diff-erent algorithms that do a better job of handling it. If you are interested in learning more you can find an example here. Exceptional diff implementations may receive karma.

Part 3: Symbolic Differentiation (45 points)

The objective of this part is to build a language that can differentiate and evaluate symbolically represented mathematical expressions that are functions of a single variable x. Symbolic expressions consist of numbers, variables, and standard functions (plus, minus, times, divide, sin, cos, etc). To get you started, we have provided the datatype that defines the abstract syntax for such expressions.

(* abstract syntax tree *)
(* Binary Operators *)
type bop = Add | Sub | Mul | Div | Pow

(* Unary Operators *)
type uop = Sin | Cos | Ln | Neg

type expr = Num of float
          | Var
          | BinOp of bop * expr * expr
          | UnOp of uop * expr

This datatype provides an internal representation of an expression that the user might type in. The constructor Var represents the single variable x, and UnOp (Ln, Var) represents the natural logarithm of x. Neg refers to unary negation and is denoted by the symbol ~. (the symbol - is only used for subtraction). The meaning of the others should be clear. Mathematical expressions can be constructed using the constructors in the above datatype definition. For example, the expression x^2 + sin(~x) would be represented internally as:

BinOp (Add, BinOp (Pow, Var, Num 2.0), UnOp (Sin, UnOp (Neg, Var)))

This represents a tree in which nodes are the type constructors and the children of each node are an operator and the arguments of that operator. Such a tree is called an abstract syntax tree (or AST for short).

For your convenience, we have provided a function parse_expr which translates a string in infix form (such as x^2 + sin(~x)) into a value of type expr. The parse_expr function parses according to the standard precedence of operations, so 5 + x * 8 will be read as 5 + (x * 8). We have also provided two functions to_string and to_string_smart that print expressions in a readable form using infix notation. The former produces a fully-parenthesized expression so you can see how the parser parsed the expression, whereas the latter omits unnecessary parentheses.

# let e = parse_expr "x^2 + sin(~x)";;
val e : Expression.expr =
  BinOp (Add, BinOp (Pow, Var, Num 2.), UnOp (Sin, UnOp (Neg, Var)))
# to_string e;;
- : string = "((x^2.)+(sin((~(x)))))"
# to_string_smart e;;
- : string = "x^2.+sin(~(x))"

For full credit, only use rec in your implementation of fold_expr. Do not use rec in evaluate and derivative.

1. Write a function fold_expr : (expr -> 'a) -> (uop -> 'a -> 'a) -> (bop -> 'a -> 'a -> 'a) -> expr -> 'a such that fold_expr atom unary binary expr performs a postorder traversal of expr. During the traversal, it applies atom : expr -> 'a to every leaf node (i.e. Var or Num). It applies unary : uop -> 'a -> 'a to every unary expression. The first argument to unary is the unary operator and the second is the result of applying fold_expr recursively to that expression's operand. Finally, fold_expr applies binary : bop -> 'a -> 'a -> 'a to every binary expression. The arguments to binary are the binary operator and the results of recursively applying fold_expr to the left and right operands.
   For example, here is a function that uses fold_expr to determine whether the given expression contains a variable.

   let contains_var : expr -> bool =
     let atom = function
       | Var -> true
       | _ -> false in
     let unary op x = x in
     let binary op l r = l || r in
     fold_expr atom unary binary
   

   
   You may use rec in your implementation of fold_expr without penalty.
2. Using fold_expr, write a function eval : float -> expr -> float such that eval x e evaluates e, setting Var equal to the value x. For full credit, do not use rec in evaluate.
   Example: eval 2.0 (BinOp (Add, Num 2.0, Var)) = 4.0.
3. Using fold_expr, write a function derivative : expr -> expr that returns the derivative of an expression with respect to Var. The expression it returns need not be simplified. For full credit, do not use rec in derivative.
   Example: derivative (BinOp (Pow, Var, Num 2.0)) = BinOp (Mul, Num 2., BinOp (Mul, Num 1., BinOp (Pow, Var, BinOp (Sub, Num 2., Num 1.))))

   When implementing this function, recall the chain rule from your freshman calculus course:

   

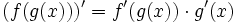
   This rule tells how to form the derivative of the composition of two functions if we know the derivatives of the two functions. With the help of this rule, we can write the derivatives for all the operators in our language:

   

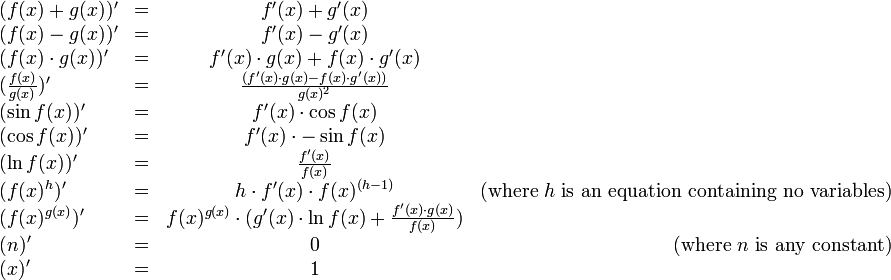
   There are two cases provided for calculating the derivative of f(x) ^ g(x), one for where g(x) = h does not contain any variables, and one for the general case. The first is a special case of the second, but it is useful to treat them separately, because when the first case applies, the second case produces unnecessarily complicated expressions.