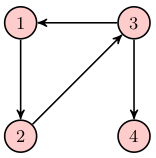
Lecture 21: Graph Representations and Traversals

A directed graph G is an ordered pair (V, E ) consisting of a set of vertices or nodes V = {v₁,...,v_n} and a set of edges or arcs E ⊆ V ². Generally we denote the number of vertices by |V | or n and the number of edges by |E | or m.

Directed graphs are commonly represented as an adjacency list, which comprises an array or list of vertices, where each vertex v_i stores a list of all the vertices v_j for which there is an edge (v_i, v_j) ∈ E.

Another common representation is an adjacency matrix, which is a two-dimensional array, where A_{i j} is non-zero when there is an edge (v_i, v_j) ∈ E. In practice, many graphs are sparse in the sense that most of the possible edges between pairs of vertices do not exist, i.e. m << n². In such cases the adjacency list is generally preferable to the adjacency matrix representation.

Edges can sometimes additionally have an integer weight, which can be used to represent distances or costs.

Here is a simple directed graph with four vertices V = {1, 2, 3, 4} and four edges E = {(1, 2), (2, 3), (3, 1), (3, 4)}.

Consider the following abstract data type for a directed graph with weighted edges. Note that while this specification does not explicitly require any particular implementation, the required running times of some of these functions constrain the implementation in various ways. For instance, a naive adjacency matrix implementation would take Θ(n²) time to consider every array entry in producing a list of all the edges. However the edges function is required to do this in O(n + m) time.

Turn on Javascript to see the code.

Note that the create function creates and returns an empty graph. The add_vertex function takes a graph as argument, adds a new singleton vertex to that graph (a vertex with no edges starting or ending at that vertex), and returns the new vertex. The function add_edge takes two vertices and a weight and joins the vertices together by an edge. These are all O(1) time operations.

The abstraction also provides operations for getting the list of vertices and edges of a graph, as well as the list of outgoing edges from a given vertex. There is also a function incoming_ref which returns a list of reversed edges, by taking all the incoming edges for a given vertex and turning them into edges that go in the opposite direction. This function is useful for exploring the back-edges in a graph (i.e., exploring the reversed graph where all the edge directions are swapped).

The Graph module in graph.ml implements this signature using adjacency lists of vertices, where both the outgoing edge list and the incoming edge for each vertex are explicitly represented. That is, each edge is stored twice, once at its source vertex and once at its destination vertex. This makes it easy to traverse the edges of the graph in reverse, which is useful for things like computing connected components (described below).

In that implementation, a graph is represented as a pair consisting of the number of vertices and a list of vertices. A vertex is represented as a triple of a unique integer id, an outgoing list, and an incoming list. The outgoing list is a list of pairs of destination vertex and weight. The incoming vertex list is a list of pairs of source vertex and weight. Note that as each edge is stored twice, in the incoming list of its destination and the outgoing list of its source, the weight must be consistent in the two lists.

In that implementation, an edge is a triple of a source vertex, destination vertex and weight, and is constructed on the fly as needed from the vertex out lists rather than being explicitly stored in the data structure.

Graph Traversals

One of the most basic graph operations is to traverse a graph, finding the nodes accessible by following edges from some starting node. You have already seen this operation in CS2110. We mark the vertices as visited when we have visited them to keep track of the parts of the graph that we have already explored. We start with a single vertex and mark it as visited. We then consider each outgoing edge. If an edge connects to an unvisited node, we put that node in a set of nodes to explore. Then we repeatedly remove a node from the set, mark it as visited, and repeat the process with that node. If we ever take a node out of the set and it is already marked as visited, then we ignore it.

The order in which we explore the vertices depends on how we maintain the set of vertices to explore. If we use a queue, so the unvisited vertices are explored in a first-in-first-out (FIFO) fashion, then the above traversal process it is known as breadth-first search (BFS). If we use a stack, so the unvisited vertices are explored in a last-in-first-out (LIFO) fashion, this is known as depth-first search (DFS).

Of course, such a traversal will only visit nodes reachable from the start node by a directed path.

Here is an implementation of traversal in a directed graph using the above abstraction. This implementation makes use of a set of vertices of type VSet to keep track of the visited vertices. It performs a BFS or DFS depending on whether the Queue or Stack package is opened. It also can traverse either the edges of the graph or of the ''reverse'' graph (in which all the edges have been reversed), based on the parameter dir.

module VSet = Set.Make (struct type t = Graph.vertex 
                        let compare = Graph.compare end)

open Queue (* use Queue for BFS, Stack for DFS *)

let traverse v0 dir =
  let disc = create()
  and visited = ref VSet.empty in
    (* Expand the visited set to contain everything v goes to,
     * and add newly seen vertices to the stack/queue. *)
  let expand(v) =
    let handle_edge(e) =
      let (v, v', _) = Graph.edge_info(e) in
      if not (VSet.mem v' !visited)
      then (visited := (VSet.add v' !visited);
              push v' disc)
      else ()
    in
      List.map handle_edge (if dir<0 then (Graph.incoming_rev v)
                      else (Graph.outgoing v))
  in
    (visited := VSet.add v0 !visited;
     push v0 disc;
     while (not (is_empty disc))
     do ignore(expand(pop disc)) done;
     !visited)

Connected Components

In an undirected graph, a connected component is the set of nodes that are reachable by traversal from some node. The connected components of an undirected graph have the property that all nodes in the component are reachable from all other nodes in the component. In a directed graph, however, reachable usually means by a path in which all edges go in the positive direction, i.e. from source to destination. In directed graphs, a vertex v may be reachable from u but not vice-versa. For instance, for the graph above, the set of nodes reachable from any of the nodes 1, 2, or 3 is the set {1, 2, 3, 4}, whereas the set of nodes reachable from node 4 is just the singleton {4}.

The strongly connected components in a directed graph are defined in terms of the set of nodes that are mutually accessible from one another. In other words, the strongly connected component of a node u is the set of all nodes v such that v is reachable from u by a directed path and u is reachable from v by a directed path. Equivalently, u and v lie on a directed cycle. One can show that this is an equivalence relation on nodes, and the strongly connected components are the equivalence classes. For instance, the graph above has two strongly connected components, namely {1, 2, 3} and {4}.

It is possible to show that the strongly connected component from a node v_i can be found by searching for nodes that are accessible from v_i both in G and in G^rev, where G^rev has the same set of vertices as G, and has the reverse of each edge in G. Thus the following simple algorithm finds the strongly connected components.

let strong_component v0 =
  VSet.inter (traverse v0 1) (traverse v0 (-1))

let strong_components g =
  let vs = ref VSet.empty
  and cs = ref [] in
    (List.iter (function (v) -> vs := VSet.add v !vs) (Graph.vertices g);
     while (not (VSet.is_empty !vs)) do
       let c = strong_component (VSet.choose !vs) in
       (vs := VSet.diff !vs c;
        cs := c::!cs)
     done;
     !cs)

Topological Ordering

Here is a simple recursive function for computing a topological ordering, which operates by choosing a vertex with no incoming edges as the first node in the ordering, and then appending that to the result of recursively computing the ordering of the graph with that node removed. If in this process there ever is a graph where all the nodes have incoming edges, then the graph is cyclic and an error is raised. The running time of this method is O(n²), whereas the asymptotically fastest methods are O(n + m).

let topological_rec g =
  let rec topological_destr gr =
    let vl = Graph.vertices gr in
      if vl = [] then []
      else
      let sl = List.filter (function v -> Graph.in_degree v = 0) vl in
        if sl = [] (* No vertices without incoming edges *)
        then failwith "Graph is cyclic"
        else
          let v = List.hd sl in
            (Graph.remove_vertex gr v;
             v :: topological_destr gr) in
    topological_destr (Graph.copy g)

Here is an iterative version of topological sort which has O(n + m) running time. Note that while remove_vertex is O(m) time for a single vertex, it is also O(m) time when all n vertices of the graph are removed, because each edge is considered a constant number of times overall in the process of removing all the vertices.

let topological_iter g =
  let gr = Graph.copy g in
  let sl = ref (List.filter
               (function v -> Graph.in_degree v = 0)
               (Graph.vertices gr))
  and revorder = ref [] in
    while !sl <> [] do
      let v = List.hd !sl in
      (sl := List.tl !sl;
       List.iter
         (function e -> 
            match Graph.edge_info e with (_, dst, _) ->
            if Graph.in_degree dst = 1
            then sl := dst :: !sl else ())
         (Graph.outgoing v);
       Graph.remove_vertex gr v;
       revorder := v :: !revorder)
    done;
    if Graph.num_vertices gr = 0
    then List.rev !revorder
    (* Remaining vertices all with incoming edges *)
    else failwith "Graph is cyclic"