fact 3 1. Note that you will need to insert approximately 10 lines of evaluation to replace the second ???:
let rec fact n p = if n = 0 then p else fact (n-1) (n*p) in fact 3 1
We have given you the following steps of evaluation:
fact 3 1 New global binding: let f' n p = if n = 0 then p else ??? (n-1) (n*p) → f' 3 1 → if 3 = 0 then 1 else f' (3-1) (3*1) → if false then 1 else f' (3-1) (3*1) → f' (3-1) (3*1) → f' 2 3 → ??? → 6
let rec zardoz l n =
match l with
[] ->
if n < 2 then failwith "try more" else 3110
| hd::tl ->
let (f,k) = hd in
zardoz tl (n+1) + f k in
zardoz ??? 0
Please refer to the notes on the substitution model for Lecture 6 and Recitation 6. We expect your steps to look similar to the examples in these pages. If you are unsure whether to include a step, it is probably better to include it. Please ask during office hours or on the newsgroup if you have any questions regarding what we are looking for on this part.
To do: Turn in the solution under SubstitionModel in CMS. Submission is allowed in .pdf, .doc, or .txt. Please do not forget to include your name and NetID in your solution.
Several algorithms, including compression algorithms and string matching algorithms, make use of maps where the keys are sequences of values of a certain type. A trie or prefix tree is an efficient data structure for implementing the map ADT for this kind of map. The set of elements from which key sequences are built is called the alphabet of the trie.
A trie is a tree structure whose edges are labeled with the elements of the alphabet. Each node can have up to N children, where N is the size of the alphabet. Each node corresponds to the sequence of elements traversed on the path from the root to that node. The map binds a sequence s to a value v by storing the value v in the node corresponding to s. The advantage of this scheme is that it efficiently represents common prefixes, and lookups or inserts are achieved using quick searches starting from the root.
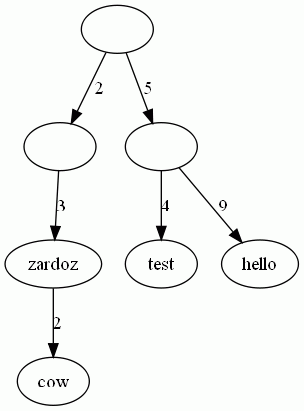
Suppose we want to build a map from lists of integers to strings. In this case, edges are labeled with integers, and strings are stored in (some of) the nodes. Here is an example:

The above trie describes the map {[2; 3]->"zardoz", [2; 3; 2]->"cow",
[5; 4]->"test", [5; 9]->"hello"}. The values are stored
in the nodes. Note that not all nodes have values. For instance, the node
that corresponds to the list [5] has no value. Hence,
[5] is not in the map.
A cursor is a data structure that points to a specific node in a trie. It is useful to define a cursor pointing into a trie when performing lookups on lists of integers in order to advance through the trie number by number.
In this part you will implement tries that map
lists of integers (int list) to values of arbitrary types ('a).
Your task is to do the following:
Interface specifications. Before you
begin implementing the trie data structure, you need to finish its
specifications in the signature TRIE. The existing
specifications may be incomplete, incorrect, or nonexistent.
Representation. You must decide how you will represent a trie. Briefly inspect the functions below to decide if certain pieces of information would make their implementation simpler. Then define an appropriate trie type.
type 'a trie = (* your implementation here *)
Next to the representation type, write comments giving the abstraction function and representation invariant for tries.
Implement the function repOK. If
the input trie satisfies the representation invariant, then repOK
simply returns the input trie. Otherwise, repOK raises
Failure.
Trie operations. Implement the empty
value, representing an empty trie, and the
functions put, get, size.
The put function adds a new mapping
to a trie. If the value to be inserted is associated with a key list
that is already bound to another value, then the code should replace this
mapping by binding the key to the new value. The function get
returns the value bound to the given key list in the trie.
If the key does not
exist in the trie, or if it exists in the trie but is not bound to
any value, then an exception NotFound must be
raised. Finally, the function size returns the number of mappings
being stored in the map (note that this is not the same as the number of nodes).
val empty: 'a trie val put: 'a trie -> int list -> 'a -> 'a trie val get: 'a trie -> int list -> 'a val size: 'a trie -> int
Cursor support. Next, define an appropriate type to describe a cursor for a trie structure. Make sure the type contains enough information to support the cursor operations defined below.
type 'a cursor = (* your implementation here *)
Implement the following functions:
val cursor: 'a trie -> int list -> 'a cursor val advance: 'a cursor -> int -> 'a cursor option val getc: 'a cursor -> 'a option
The function cursor returns a
cursor positioned at the node that corresponds to the int list given as an
argument. If the list doesn't exist in the trie, the exception NotFound
is raised. The function advance moves the cursor one
position down the tree, following the edge that corresponds to the integer
passed as an argument. This function returns None if no
such edge exists. The function getc yields the value stored
at the node that the cursor points to.
To do: Turn in the solution in the files
trie.mli and trie.ml.
T9 is a technology used on many mobile phones to make typing text messages easier. The idea is simple - each number of the phone's keypad corresponds to 3-4 letters of the alphabet. To type a word like "TEST", you type the keys 8-3-7-8 corresponding to these letters. The phone then searches an internal dictionary for any possible words of the form {TUV}-{DEF}-{PQRS}-{TUV}, of which "TEST" is the most common (or only) word. Most phones use additional intelligence to improve performance of this basic algorithm. For example, many phones will notice when you type in a word that is not in its dictionary, and will add that word. Others keep track of the frequency of certain words and favor those words over other words that have the same sequence of keypresses.
Your task in this problem set is to implement a basic T9 algorithm. It will be particularly imporant in this exercise to choose data-structures that are well-suited to the following features that we are asking you to implement.
This T9 algorithm will have a word count associated with each of the words in its internal dictionary. When words are suggested, words that are used more often are suggested before rarer words that may fit the entered keystrokes, but are less common. Likewise, when a candidate word is selected, this internal word count must be increased.
The T9 module also behaves much like a state machine. At any point in time, it will have processed a certain set of
keystrokes. If a new keystroke is entered by calling enter_digit, the returned T9 object should have
its internal state updated to reflect this. Likewise, when suggest_next_word is called, the returned
object should keep track of this fact and suggest a different word when this function is called a second time on the
new T9 object.
In the file t9.ml,
you will need to implement the following functions:
(* An empty T9 object, at the initial state of no characters entered. *) val empty : t9 (* update t9 w adds w to the T9 object if it does not exist, or increments * the count by one if it does. *) val update_word : t9 -> string -> t9 (* enter_digit t9 n attempts to return a T9 object in a new state, with * the digit n typed. If no words can be formed after adding this new digit, * the input T9 object should be returned unchanged. *) val enter_digit : t9 -> int -> t9 (* suggest_next_word t9 returns the next candidate word for completion at the * current state of the input T9 word set, as well as a T9 object with the * state updated to reflect this. *) val suggest_next_word : t9 -> string option * t9 (* choose_word t9 confirms the selection of the current word, incrementing * the frequency count and restarting the selection process *) val choose_word : t9 -> t9
The specifications for these functions is given in the included .mli file, which you should not modify. Your first task is to determine an appropriate type for the T9 object. Remember that you must maintain an efficient dictionary data structure as well as an internal state that allows keystroke-by-keystroke traversal of that dictionary. Be sure to think about how to implement all of the above functionality given your choice of data structure, before you write too much code.
We will also provide you a file dictionary.txt that contains all of
the words we want you to search for. You will need to complete the module
dictionary.ml in which you read the dictionary into a new T9 object.
The capitalization of the words of the dictionary should be maintained.
To read in the dictionary, you will need to use file I/O. A nice tutorial on reading and writing files can be found here. You can also check out the OCaml documentation here. All of the provided files can be found on CMS.
Good luck and get started early! Please use the newsgroup or come to office hours if you have any questions.
To do:
Turn in the solution in the files
t9.ml and dictionary.ml.
Use the trie you wrote to implement a function
sort: string list -> string list that sorts a list of strings
in lexicographical order. It must have O(n)
complexity, where n is the sum of the lengths of
the strings (assuming the alphabet is of constant size). This may require a fair
number of modifications to trie - you should copy whatever code you need into sort.ml
and make your modifications there instead of modifying trie.ml.
To do: Turn in the solution in the file
sort.ml.
In this part, you will consider how one might type-check OCaml expressions, by implementing a simple type-checking algorithm for a subset of OCaml. The language is defined as follows:
type mytype =
MyInt (* Represents the type int *)
| MyTuple of mytype list (* The type of a tuple. MyTuple(t1;...;tn)
* corresponds to the type t1*...*tn. *)
| MyUnit (* The type of an empty tuple (). *)
type exp =
Int of int (* An integer constant. *)
| Tup of exp list (* A tuple expression. Tup[e1;...;en] represents
* (e1,...,en). Note: Tup [] represents () and
* Tup [e] represents (e) = e. *)
| Proj of int * exp (* Tuple projection. Proj(n,e) evaluates to the
* nth element of tuple e, with element indices
* starting from 0. *)
| Plus of exp * exp (* Adds two integers. *)
| Let of string * mytype * exp * exp
(* Let(s,t,e1,e2) defines a variable with the name s, type t,
* and value of e1 and uses this new variable when evaluating e2. *)
| Var of string
(* Var(s) represents a variable named s, which should be
* defined earlier in a Let *)
Complete the function:
fun typeCheck (e : exp): mytype = ...which takes an expression of type exp, and returns the expected type of the value produced by this expression.
A few examples:
2+3 is represented as Plus(Int 2, Int 3). Calling typeCheck on this returns MyInt.List.nth (5,6,7,8) 2, which evaluates to 7, is represented as
Proj(2,Tup[Int 5; Int 6; Int 7; Int 8])), which type-checks as MyInt.typeCheck(Tup [Int 4; Int 5]) results in MyTuple[MyInt, MyInt].typeCheck(Let("x",MyInt, Plus(Int 3, Int 6), Plus(Var "x", Var "x"))) returns MyInt.Implement static scoping for variable resolution (HINT: Define a type environment that records the types of bound variables in an association list).
Some expressions cannot be type-checked, e.g., Plus(Int 2, Tup[Int 3; Int 4]). You should fail with a useful description
of the error in cases where the expression does not type-check.
There is a bit of awkwardness caused by our use of OCaml lists in defining tuples, since lists can be length 0 and 1,
but tuples cannot. Length-0 tuples should be of type MyUnit, so that typeCheck(Tup[]) returns MyUnit. For length-1
tuples, return the type of their one element; e.g., typeCheck(Tup[Int 3]) returns MyInt.
To do: Turn in the solution in the file
typecheck.ml.