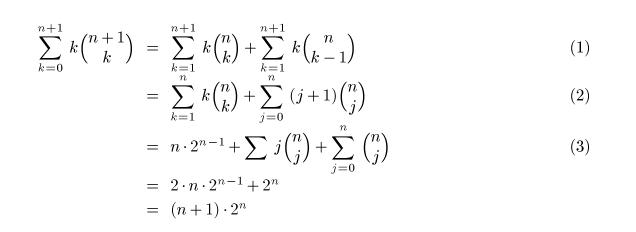Common mistakes in Problem
Sets
Common Mistakes
in Problem Set SIX
Problem 1 (Tom) [4 points]
Two points were assigned to each part, with one point
for the correct answer (true/false) and one point for the proof. Few people had
trouble with this problem. One thing to note is that you don't know that sets
form an algebra over union and intersection -- that is, you can't claim without
proof that A intersect (B union C) = (A intersect B) union (A intersect C). This
is easy to show, either by considering an element of each side in turn, or using
set-builder notation, but you need to show it.
Also, while we did accept Venn diagrams as proofs for
this problem, there exist problems where it is effectively impossible to
consider all possible arrangements of the sets (e.g. with 4 sets you might need
to consider as many as 65536 arrangements). In general, a mathematical proof is
safer than one involving Venn diagrams (though the diagrams remain invaluable
tools for thinking about the sets).
Problem 2 (John) [3 points]
I think everyone pretty much knew the answer (I recall
only one person getting it wrong) but a number of people had problems with the
proof.
The most common error was the thought that Pascal's
triangle showed that it was the middle without relating Pascal's triangle to the
problem, or doing induction on it.
Problem 3 (Yogi) [4 points]
Most of the students got this problem
right, and those who did not got almost no credit. A very few students were
there who made some small mistakes and hence got only a partial credit.
-
One mistake that many students made
(and I did not take off points for that) is that they did not explicitly
mention that {n \choose -1} is zero or {n \choose n+1} is zero. The best
thing was to drop the term corresponding to k=0 in the summation (as it had
multiplication with k), otherwise, the cases of choosing negative number of
items should have been handled correctly.
-
Some students did the proof by
induction, and
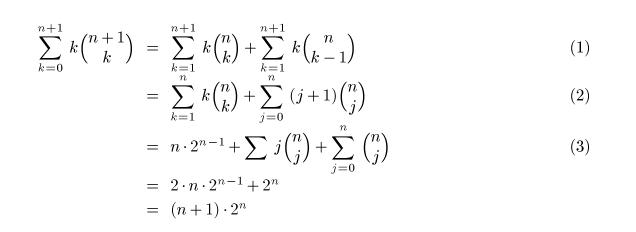
were not comfortable with the step 2 where we substitute k-1=j. If you went
only will step 1 above, you collected 2 points (out of 4 possible).
Problem 4 (Tom) [3 points]
The intention was that one point be given for the
answer, one for an example when the maximum is attained, and one point for the
proof of maximality. Due to a misunderstanding, the actual rubric was one point
for the answer and two points for the proof. This was applied across the board,
with the result that almost all grades were 1 point harsher than intended. I
apologize for this, but the grades are all consistent; as a result, please do
not ask for a regrade just because you did not get credit for including an
example. You should still submit a regrade if you feel there is any other
problem with the grade.
The biggest problem that people had was in proving their
answer of n correct. The following argument does not suffice: "Let A be the
collection of all singleton sets; then |A| = n. And if we create A' by adding
any other set to A, there will be two sets which overlap, disqualifying A'. Thus
A is optimal." The issue here is the assumption that A is a subset of A',
which is not necessarily true. A proof needs to consider all possibilities for
A', not just those A' which resemble your A. The heuristic argument "any
set which has more than one element 'eliminates' more elements than it needs
to" is a good way to think about the problem, but should be made more
rigorous. A pigeonhole argument could be made to work if you were careful about
what you were claiming.
Problem 5 (Kevin) [4 points]
1 point for getting P(n,k) correct.
1 point for getting F(n,k) correct.
1 point for the explanation of P and F.
1 point for giving the correct answer for F(n,k) when
k=1 and when k=2.
The most common mistake on this problem was either
explicitly or implicitly assuming that the order of the purchases doesn't
matter. The problem was dealing with "sequences" and
"histories", so order did matter. Since it wasn't outright stated in
the problem that order matters, only one point was deducted for making this
incorrect assumption if the rest of the analysis was correct under that
assumption (P(n,k) = nCr(n + k - 1, k) and F(n,k) = n^2).
Many people didn't cover the case when k=1 or when k=2.
The general answer for F(n,k) is actually incorrect for these two cases, so they
needed to be discussed separately.
Some people forgot that a highly focused history also
includes cases where all the genres are the same. This means you need to add (n)
to your term (n(n-1)k). Also, some people forgot to multiply (n(n-1)) by k to
account for the odd-man-out genre being placed in any position of the sequence.
Problem 6 (Joel) [4 points]
There are two mistakes that were very common. It was
neccesary to show that 2^{n-1} was both an upper bound for the size of Q, and
that it was attainable. In other words, you need to show that you can get
2^{n-1}, and that you can't do better.
Problem 7 (Yogi) [Optional 0/1]
This was a difficult problem compared to
the last problem sets' optional problem. There were three parts to the problem,
and computing s(n,k) was the most difficult. Unfortunately, due to the grading
scheme on optional question, if you attempted two easy parts but did not find
the expression for s(n,k), you did not get the credit. Some common pitfalls were
the following:
-
Some students said that they found the
particular formula with ``brute force'' and wrote that as their answer. You
were needed to supply the proof/argument how you got the particular
expression for s(n,k), failing which you did not receive any credit (even if
your expression happened to be correct).
-
Some student made the mistake that they
said that we can select n-2k position in just n-2k+1 ways because they could
either be all one, or all zero or 1's followed by zeros. This is true if you
are not allowed to break up this set of n-2k positions. But these n-2k
position could have been divided in k+1 continuous chunks, and hence the
above argument works for each of those chunks, but not for all n-2k
positions. We have to take care of number of ways in which n-2k position can
be partitioned in k+1 parts.
-
Please see the solutions (available on
CMS) for further
details.
Common Mistakes
in Problem Set SEVEN
Problem 1 (Tom) [3]
Almost everyone got this right. A few
people used the division rule, but instead of dividing by (3!)(3!)(2!)(2!)=144,
divided by (3)(3)(2)(2)=36. Also, some people went through the problem letter by
letter, putting in the 3 E's, then the 3 S's, etc. This gave the right answer
(and most people did it correctly), but it requires a lot more work, and it's
easier to make a mistake.
Problem 2 (Yogi)
[3]
Students did very well on
this problem (so there are not many "common" mistakes as such). Some
of them are:
-
The off-by one problem was there. Some
students forgot to subtract one from blocked configuration (one state in
which all processors are done is not blocked).
-
A couple of students thought that the
ordering of the processors does not matter (they took processors as
indistinguishable). It was not very clear from the question whether ordering
matters, but in case of doubt, you should make it clear in office hours, or
atleast state the assumption in the answer. Anyway, the problem was more
difficult if you do not take ordering into account, and you did get credit
if you thought the processors as indistinguishable.
-
Some students gave the answers for
particular values of n, say for n=3, n=4 etc. The question asked the
expression in terms of n (and not for any particular value of n).
Problem 3 (Zach) [2+2]
This
problem was worth four points, two for each part. To earn full credit, you
needed to have given a correct answer, and a valid explanation. The
explanation was worth 1 point, and the correct answer was worth 1 point.
For
number 3, the biggest problem I saw was lack of explanation in derivation of the
answer. You needed to have given a clear reason why the number of
multiplexed streams is the same as the number of ways of rearranging aa...abbb....b,
etc. Many people just used this, but did not say why the two numbers are
the same.
Problem 4 (Hari, John)
[5]
Check the final solution you give closely. It will help
you show that is satisfies the properties, and it will prevent a silly mistake
by giving a solution that can easily be broken. If you find that your solution
can be broken, you likely did the whole problem wrong.
Also, be rigorous with a proof. Don't give an example of
how the scheme fails and say that the example proves it. DON'T cover huge swaths
of your proof with things like "obviously" and "from this it
clearly follows" unless it REALLY clearly follows. If you have a doubt just
put in a line explaining why it is so clear.
Problem 5 (Tom) [3]
Most people received full credit for this problem; it
was very easy, requiring one short application of the inclusion-exclusion rule.
Relatively few people did it correctly, though; many
people had problems with the definition of an event and even a sample space.
Please see the solutions, as less than 20% of the class
correctly identified the event. The event is not the sentence "5 | k or 7 |
k".
The event is a set, and it is a subset of the sample
space. Some people gave heuristic arguments, which was all right, but then
neglected to mention the sample space or event at all. We were very lenient
regarding probability and proofs on this first homework, but until you have the
concept of independent events, truly correct heuristic proofs are almost
impossible.
Problem
6 (Kevin) [2+2+2]
Nearly everyone
got these right. The only mistakes were
-
leaving out a description of the sample
space (which was actually all possible results of throwing k dice, but we
accepted anything reasonable) and
-
forgetting to filter out all events
which didn't meet the criterion, i.e., that the sum of the first two dice is
7 or that the sum of the first three dice is 8.
Problem 7 (Joel) [0/1]
The
most common mistake was not using the proper definition of the Quorum system
from the previous assignment.
Only
very few students got this problem right. Given that the problem was
comparatively easier then the optional problem of other problem sets, it seems
that students have stopped attempting the optional problem. The students should
atleast try to attempt the optional problem...
Common Mistakes
in Problem Set EIGHT
Problem 1 [3] Joel
The only mistake on problem one was to fail
to mention that you were calculating the expected number of votes for democrats,
not the actual number.
Problem
2 [4] John
On this problem most people knew how to compute the answer
to the problem, and the rules for the conditional probability were pretty well
understood.
However, a great many people mistook the sample space to
be emails from hotmail rather than all email to Cornell.
Problem 3 [2] Tom
Every single person did this problem
correctly. A handful of people made arithmetic mistakes, but were still doing
the right thing. It can be a good idea to check your answers to make sure they
make sense -- if you get something that isn't anywhere near what you expected,
try going through your calculations again.
Problem
4 [7=4+3] Hari
For the most part, people seemed to get this. However, there were a few problems.
-
People said that the probability of one machine getting into S is
1/2^(d+1) so the expected number of machines getting in is n/2^(d+1). While this is true, you have to make some reference to the linearity of expectation. If this
statement was not properly justified they were given the comment "Why?"
-
The only real problem here is that people didn't follow directions and many forgot to give the Expected number of machines in S given the value of p they derived. For this they
received the comment "E(X)?" Also, points were not taken off for people who did the calculus wrong.
Problem 5
[8=1+2+2+2+1] Kevin (black fonts), Zach (blue fonts)
-
Most people got this part right.
No comments.
-
The most common error was forgetting to multiply 1/k * (1 - 1/k)^(k-1) by k; this is necessary because each computer can receive any of the k different jobs. Without this extra coefficient, you found the probability that a given machine receives exactly some pre-specified job.
Many people started out correctly and yielded (1/k)(1-1/k)^(k-1). But, this is the probability that a given job i, goes to machine j, and the other k-1 jobs
don't go to machine j. The problem with this is that there are k choices for i, so we must multiply through by k. This yields (1-1/k)^(k-1).
-
A lot of students tried to take the k-th power of their answer for part (b) as their answer for part (c). This is not right because the event that some machine gets exactly one job is not independent of the event that some other machine gets exactly one job. The best way to approach this problem is to notice that there are k^k ways of assigning jobs to processors, and k! of these ways result in one job per processor. So the correct answer is k!/k^k.
A lot of students tried to prove that it converges to 0 by noticing that the numerator is always smaller than the denominator. This does not prove convergence to 0, e.g. consider (k-1)/k. This converges to 1. You could have shown that k!/k^k is bound by 1/k, which goes to zero, or you could have used the ratio test.
For this, many people took the answer from b) and raised it to the kth power, using the rationale that the probability of a machine getting one job is (1-1/k)^(k-1), so the probability that machine 1 gets one job and machine 2 gets one job,..., and the probability that machine k gets one job is just ((1-1/k)^(k-1))^k. This is not correct, as the probability that machine a gets one job is not independent of the probability of machine b getting one job (because if machine a gets a job, there is one less job for b to be able to get so the probability is no longer (1-1/k)^(k-1)). What we do instead is to say: there are k^k ways to distribute the k jobs (each job has a choice of k machines), but only k! ways with each machine getting one job (job 1 goes to one of k machines, job 2 goes to one of k-1 jobs, etc.), so the probability is k!/k^k.
Now, in proving that the limit of k!/k^k = 0 as k -> infinity can be done in several ways, but it does not suffice to say that the denominator is growing faster than the numerator as this is not rigorous and does not actually prove that the answer is 0. It is easier to say:
k!/k^k = 1/k * 2/k * ... * (k-1)/k * 1 <= 1/k as each of the other terms in the product are <= 1. Therefore, limit k!/k^k <= limit 1/k = 0, and we get the result as k!/k^k is nonnegative for each k.
Also, some people tried using the ratio test which does work, but the ratio test is used only for infinite sums, so it only works in this case by careful analysis. Using the ration implies that the sum from 1 to infinity of n!/n^n converges. And as it converges, its terms must go to 0, so limit of n!/n^n -> 0. Try to stick to more conventional ways of proving limits like comparison and algebra.
-
By the linearity of expectation, we can just multiply our answer from part (a) by k. Otherwise, this quantity is not difficult to calculate directly; most people got it right.
The biggest mistake I saw was that people misread the question and tried taking the limit of N(k), while the question asked for N(k)/k which converges to 1/e.
-
Everyone should have realized that R(k) = N(k). Without this fact, it is very hard to find the value of R(k) directly. Few people did so correctly.
The trick to this problem, and the only sensible way to do it by avoiding horrible calculations, is to notice that R(k) = N(k), because the number of rejected jobs equals the number of machines with 0 jobs, since if a job goes to a machine which has a job already, then some other machine cannot receive that job, and as the number of jobs equals the number of machines we get that one machine must not receive anything. Extending this argument to all the jobs gives the result.
Problem
6 [0/1 Optional] Yogi
Not many
students attempted the problem but the statistics were better than the last time
(for optional problem). The common mistakes were the following:
-
Some students just mentioned their
strategy without any justification or proof. They mentioned a sequence of
steps that the seller should take (without any justification), and sometimes
the steps were not even exhaustive (they did not cover all the cases). In
such cases, no points were awarded.
-
Some other students tried analyzing the
strategy, went quite far inside the explanation and proof, got some
complicated expressions and then just said that the expression they got is
greater than 4 (again without justification). Please note that you should
provide justification to all the steps you write unless the step is
completely obvious/trivial.
-
There was one common mistake about the
independence of the events. If the highest bid is in the second half of the
sequence, then the probability of second highest bid being in the first half
is not 1/2 but a bit more then that which is n/(2(n-1))>1/2. But we did
not take of (sole) point for this mistake. But please be careful when you
multiply two probabilities, the events have to be independent to multiply
the corresponding probabilities.
-
Just a final note which is not specific
to this problem but applies in general. Students are (sometimes) doing
addition/multiplication of probabilities in an ad-hoc manner, without
justifying the operation. Please convince yourself before the operation you
do. For addition of probabilities, you need the events to be disjoint and
for multiplication, the events must be independent. It might not be very
crucial (to understand all this) now, but once the problems become complicated enough, your arguments
needs to be sound.
Comments
for Prelim 2
Problem 1 (3) Eva/Hari
Despite
the close similarity with Question 5 from Problem Set 6, many people
did not think of handling separately the cases when fewer then 3 genres are
involved in a sequence. This lead to overcounting the possible solutions.
Also many people did not handle short sequences separately: when
k=3 or smaller, all sequences are almost focused, and the formula derived
for higher values overcounts this. In fact, there is even a case where k=4
has to be handles separately. Very few people noticed this fact, and we did
not subtract credit for this.
Problem 2 (3)
Hari
People who approaches this with induction tended to get
it right. Some people didn't use Pascal's theorem in the inductive step and
ended up doing a good amount of needless algebra, but points were not taken off
for this.
A few people tried some combinatorial arguments. While
this can work (see the solutions) only one person did this correctly.
A good number of people tried the straight algebraic
argument. Often times people would manipulate the left side of the equation and
after a couple of steps, would magically deduce that the expression they had was
equal to the right side. Points were deducted for jumps in logic such as this.
Problem
3 (3) Tom
Most people who made mistakes on this problem gave one
of the following answers: "100^3"; or "C(100,3)"; or
"C(100,3) + C(100,2) + C(100,1)". The correct answer was
"C(102,3)" and can also be written as "C(100,3) + 2*C(100,2) +
C(100,1)", "100 + 100*99 + 100*99*98/6", or "171,700".
There were other correct ways to write the answer.
The answer "100^3" comes from not realizing
that order doesn't matter; the answer "C(100,3)" comes from not
realizing that items could be repeated; the answer "C(100,3) + C(100,2) +
C(100,1)" comes from not realizing that "banana,banana,apple" is
different from "banana,apple,apple". These responses all warranted
partial credit.
Problem
4 (8) Tom
- Many people over- or under-counted the number of ways
this could happen by 1. I tried to give partial credit if it was clear that
this happened. The answer should not have involved the ceiling or floor of
anything.
- The reasoning we were looking for was a justification
along the lines of "by the linearity of expectation", or perhaps
an explicit "E(X+Y)=E(X)+E(Y)". The computation was fairly easy,
though many people computed E(X) as n/2 rather than (n+1)/2. Also, it does
not suffice to show that you can get n+1 in more ways than anything else.
It MIGHT suffice to show that the distribution is
symmetric about n+1, but we don't have the tools in this course for that
(and it's not necessary).
- This followed from part (a), and indeed even if you
got part (a) wrong, you still should have gotten
full credit for this problem if you computed it correctly based on your
answer to (a). Note that Bayes' formula could be used here (though you
didn't need to), but most people who tried Bayes' formula made mistakes.
Problem
5 (11) Kevin + Zach
I really
don't have any informative comments for my problem, other than to read the
solutions.
Problem
6 (12=4+4+4) Joel + Yogi.
The
most common mistake was to forget n! or 2^n in the formula for number of pairing
(correct formula is (2n)!/(n!*2^n)). This was mainly because some of the
students did not consider that the ordering of all the pairs does not matter (it
does not matter whether I call the pair of (A,B) first pair of i th pair).
Some
of the students misunderstood the question to find the number of possible pairs
that we can select from 2n students... the answer to that is clearly {2n \choose
2} and the problem became very easy after that. The maximum credit you got (in
part a. and b. combined) after you made this mistake was 3/8.
Some
students made the mistake in third part by summing the expectations for
only n students. The expectations were to be added for all 2n students. You lost
one point for this mistake.