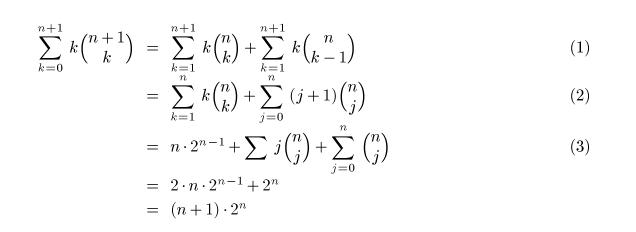Common mistakes in Problem
Sets
Page last updated: Thu Oct 09 2025 00:33:52 GMT+0000 (Coordinated Universal Time)
Common Mistakes
in Problem Set ONE
Problem 1: (2+2)
Problem 2: (2)
Nearly everyone got these questions correct. The only
somewhat-common problem was that some people didn't seem to realize that F
-> T = T and F -> F = T, i.e., a conditional statement with a false
premise is always true.
Problem 3: (2+2+2)
The common mistake was to misunderstand the meaning of
"who satisfies Rule 1 but does not satisfy either Rule 2 or Rule 3".
It means that the person should satisfy rule 1 and should neither satisfy rule
2, nor rule 3. Some students took it as the person should satisfy rule 1 but
does not satisfy rule 2 or does not satisfy rule 3 (which is not correct). One
point was taken off for that.
Another misunderstanding was regarding the meaning of
Art. Some took it as Arts and Science School while others took it as
Architecture. Actually it was intended to be another identifier (and no meaning
should have been attached to it). No point was taken off if you solved the
problem with your interpretation.
When A does not imply B, it means that if A is true, B
might not be true. It might be true also. So, the statement that "B cannot
be true" is not correct. It should be "B might not be true".
Problem 4: (2)
In problem 4 the most common problem seemed to be that
people forgot to say that the two machines were different. Remember, if you say
ExEy....
then it DOES NOT automatically mean that x and y are
different.
Also, some people said things like
(ExP(x)) AND (EyP(y)) AND (x != y)
I did my best to be lenient about parenthesis but in
this case it is clearly wrong. The first part
(Ex(P(x))
is a completely encapsulated statement, the Ex does not
apply to the other two parts because of the parens. What you wanted to write was
(ExP(x) AND (EyP(y) AND x != y))
But I also accepted thigns like
ExP(x) AND EyP(y) AND x != y
assuming that you would have gotten the parens right if
you had tried to.
Problem 5: (3)
Common mistakes were to forget to mention that the
solution is not unique, for which I deducted 1 point. Also, people just got the
answer wrong, which cost them between 1 and 2 points depending on the severity
of the mistake (I don't believe anyone received no credit).
Problem 6: (4)
If you got the correct counter example in a suitable
form you got 4 points. The biggest problem I saw is that some people thought
that circuits had to be Trees, but this is not the case.
If you proved it for the tree case I awarded 2 out of 4
points.
Problem 7: (4)
Feedback: most of the points were taken off for not
explaining why *all* the variables were influential, and just giving one. some
seemed to think that to be influential, a variable had to change the truth value
of the formula in all possible truth assignments, which is not true (there just
needs to exist one). some those who did get the problem right failed to take
advantage of the inherent symmetry in the problem.
while this solution was acceptable, a simpler solution
was preferred.
Problem 8: (Correct or Incorrect 0/1)
"Approximately half the students attempted this
problem, of which perhaps half received credit. Apart from only solving the
question for positive coalitions, the two most common problems were a) trying to
guess the expressions from trying a few simple cases without proving anything,
and b) assuming that the expressions for negative coalitions would be just the
reverse of those for positive coalitions.
In the former case, even if you manage to guess the
correct expressions (most people didn't), without a proof your solution can
receive no credit. In the latter, running a simple check with small numbers
would have shown that the expressions are slightly different.
Just as examples without a proof are only good as a
starting point in finding the formula, a theoretical proof without checking your
results leaves you open to simple errors or mistaken assumptions.
Many people received no credit despite completing half
of the problem; this is because optional problems are graded all-or-nothing. In
general, almost everyone who correctly found (and proved!) the expressions for
the size of the coalitions received credit. Given the fact that these problems
are completely optional, worrying too much about whether or not you received
credit is not necessary. (If you feel a mistake has been made in grading on
other problems, follow the procedure for getting a regrade.)"
Common Mistakes
in Problem Set TWO
Problem 1: (1+1+1+1+1+1=6) Hari
The most common problem was people didn't
follow directions and used logic instead of english.
Problem 2: (1+1+1=3) Joel
For problem 2 there were basically no common mistakes,
since getting it wrong was extremely uncommon.
For problem 7, I'd say one common error was do use a
reverse implication in the inductive step without explicitly stating it (i.e.
working backwards from what you're trying to prove).
Problem 3: ()
Problem 4: (4) Zach
As far as grading is concerned, Most people
got my problem right, but did not know how to write a correct proof. So I
took off 1 point for each major style mistake. One big flaw that I saw
across a lot of papers is that they wanted to show expression A equal to
expression Z
so what they did is (capital letters are expressions)
A = Z
B = Z
C = Z
...
Z = Z
this is only correct if you put if and only if after each line, and in the
future they instead should do A = B = C = ... = Z.
Also, people should realize that P(n) is about a particular n, not all n.
Problem 5: ()
Problem 6: (6) Sam
The biggest difficulty people had with
this problem was the algebra in the induction step. this is the first induction
homework, so it is expected that proper form for inductive proofs is still being
learned, but I won't discuss that here. specifically, the most common mistake
was that people used the inductive hypothesis in the wrong place. in terms of
logic, reducing something to a true statement does not make the original
statement true. it must be noted that in an inductive proof of this sort, the
implications between statements are directed from later statements to earlier
ones, not the other way around. for example, if I need to prove that a >= b
given a >= c, saying that b > c, and thus a >= c does not show that a
>= b: the implications go in the wrong direction.
Problem 7: (2+4+3) Kevin, Yogi
Most people tried to prove parts (b) and/or (c) without
induction. Since it was not required, we were lenient with the grading, but
most of them were not very rigorous. It is better to use induction for those
types of problems, since it is important to know the basic structure of the
proof and to become comfortable with inductive proofs. Using the inductive
approach forces you think hard about the logical connections between your
statements and how they lead to the conclusion, rather than just putting some
ideas down on paper.
One more thing that I saw in some of the solutions is
that students were putting down induction hypothesis but never using it.
Instead they said that the player will win "eventually" proceeding
in similar fashion... but this is the precise reason we use induction, to
formalize this "eventually".
Overall, almost everyone got the correct intuition behind
the solution.
Problem 8: [Optional--Correct or
Incorrect] Tom
I saw few problems among those who turned
in solutions. Anyone who correctly found the squares from which player 1 cannot
win, and provided justification, received credit. A few people did only the
first steps, then stopped, missing 2 squares from which player 1 loses. Two
people misinterpreted the problem as "whoever moves onto the goal square
loses". Credit was awarded, as this is an equally interesting problem ---
but this reversal of the goal changes the solution completely. We were hoping
that someone might find a general formula, but no one did.
Common Mistakes
in Problem Set THREE
Problem 1 (1) Zach
Problem 2 (2) Zach
There are no general comments for 1& 2,
it was for the most part all or nothing.
Problem 3 (4) Tom
Most people are comfortable with a problem like this by
now. Almost everyone recognized that strong induction was the way to go (though
a few people correctly proved the statement using only weak induction), found
the necessary base cases, and proceeded correctly through the inductive step.
The majority of points were lost from sloppy mistakes, rather than flaws in the
idea.
Most commonly, some people again put a "for all n
in N" statement inside of P(n). This is never correct.
"P(n): for all n in N, n >= 12, a team can score
n points."
This is wrong (nonsensical!), and lost you some credit.
Just say
"P(n): a team can score n points". You will
then only _prove_ P(n) for n >= 12, but that's better done in your proof than
in P(n). The other problem, which appeared far too often, was treating P(n) as a
number.
This is bad, but understandable, when P(n) is the
correctness of some formula for n. But in this case, when P(n) is just a
statement, it makes no sense to write the following:
P(n+3) = P(n) + 3
n+1 = P(n-2) + 3 = 3a+7b + 3
This is a "type mismatch", in a way: P(n) is a
statement, and you can't add 3 to a statement. Be clear about where you assume
P(n), where you conclude P(n+3), and where you're just doing algebra.
Problem 4 (4) Yogi
There were many small small mistakes
students made in this question.
One mistake was that many people wrote that
P(0) for k=0 is H(2^0)<=1+1. The right hand side should have been 0+1 as it
is k+1 and for k=0 it is indeed 0+1. Some students started the base case at k=1
which is NOT correct as we were to prove the statement for all k greater than or
equal to 0.
Some students forgot to attempt the second
part in which we were to prove that H(n)<=ceil(log n+1). Others said it is
obvious and did not prove. Obviously, no points were awarded in such
cases.
Others said that taking k=log n and using
the first part gives the result. This is also wrong as log n may not be an
integer while first part was proved only for integers. No points were awarded if
you made this mistake. The correct proof is
H(n) = H(2^{log n}) <= H(2^{ceil(log
n)}) <= ceil(log n)+1
where the last inequality follows from
first part (part a) and log is base 2.
Another mistake that some of the students
made was that they wrote
H(2^k)=1+1/2+1/4+1/8+1/16+...+1/{2^k}
which is clearly wrong. Nothing remains to
prove if you made this mistake.
One more mistake that a couple of students
made: they wanted to prove that if 2^{k-1}<n<=2^{k} then ceil(log n)=k.
This is true. But they showed that the inequality above holds for n=25 and hence
it is true. Proving inequality for one integer in no sense imply that it will
hold for other integers also...
Problem 5 (5) Hari/Joel/Sam
The biggest problem that people had when doing this
problem was that they assumed (explicitly or implicitly) that just because some
element satisfied B'(X), there must be a ranked order of all the elements
according to the majority preferences. This is not true! In fact, this is
exactly what the statement of the problem said was not necessarily true with
respect to B(X). If we define the two step preference needed for B'(X) as
X>Y, meaning X is either in one step or two steps preferred to Y by the
majority, then if X > Y and Y > Z, it is NOT necessarily true that X >
Z. This transitivity is what would make a ranked order necessary. So, most of
the points on the problem were lost a proof went along the lines of inserting
the new (n+1)st element (in the inductive
step) somewhere into "the list" or "the
ranked order" or "somewhere below the previous winner in
preferences". There is more that needs to be said.
Problem 6 (4) Kevin
The most common mistake was that a lot of people didn't
use the definition of a rational number in their proof. Instead, they reasoned
like this: "An irrational plus 1 is still irrational. The square root of
an irrational is also irrational. So a(n+1) must be irrational." This
proof was perfectly acceptable, but only if you showed some justification
of those two facts. Also, many people cut their inductive proof short
after showing that P(n) implies P(n+1). You need to finish with a conclusion
asserting that your claim is true by math induction. Also, be sure to
explicitly mention where you use your inductive hypothesis. Some people used
the fact that a(n) is irrational without mentioning that this is
true only because of the IH.
Problem 7 (Correct or Incorrect)
Zach/Sam
For the optional problem, first off, a lot
of people did not know what closed form meant. A closed form expression
f(n) is an expression involving n, which does not rely on any other values of
f(i) for i not n. For example a summation is not typically a closed form
expression.
Also, you were not allowed to assume the recurrence relation r(n) = r(n-1) + n,
you had to justify this. This problem is also all or nothing, so any
mistake got a 0.
Common Mistakes
in Problem Set FOUR
Problem 1 (2) Kevin
Nearly everyone got that the GCDs were 1 and 12. However,
most people forgot to answer the second part of the question: writing the GCDs
as a linear combination of the two numbers. This was a straightforward
exercise, given that you'd already done Euclid's Algorithm to find the GCDs.
Problem 2 (3) Hari
For the most part, people got problem 2
correct. The most often made mistake was that people forgot that multiples
of 25 each contribute 2 zeros at the end of the number, not just 1.
As a side note, some people solved this problem by writing out all the numbers
from 1 to 99 and counting the multiples of 5 and the multiples of 25.
While this method works, these people should read the solutions posted since its
possible that you might be asked at some point "how many zeros are at the
end of 999!" and then you dont want to write down every number from 1 to
99.
Problem 3 (4) Joel, Sam, Yogi
This was the most difficult question on the problem set
for most people.
The most common mistake was to improperly do the
induction step when involving powers of 3 into P(n). The problem basically
boiled down to the fact that when trying to invoke the IH, it was not
obvious/trivial that the k for which P(k) was assumed to hold was in fact in the
IH. It followed directly from the fact that the sum of the powers of 3, i.e.
\sum_{i=0}^{n} 3^i, is equal to ( 3^(n+1) - 1 ) / 2.
However, few people mentioned this fact and hence their proof was invalid.
Besides two solutions given in the solutions, there is
another solution in which we can convert base 3 normal representation to the
representation in question. Some students did it but failed to prove that this
conversion works correctly, in particular that this conversion does not produce
any duplicate powers. The solution was assumed to be "half correct"
only.
While forming the induction hypothesis, some (rather
many) student just said that a number up to certain limit can be represented by
difference of powers of three, without mentioning how many powers of three are
needed, that is what is the highest power used in the representation. Students
using this "weaker" induction hypothesis did not prove that the powers
of 3 are not duplicated... and hence the solution was not entirely correct.
Some students did not know what the base case was, so
they tried to prove for n=0, 1, 2 and up to some finite number (typically 3 or
5). For determining the base case, you should go to the induction step and see
which lower values of n do you need and prove the base case for so many values
of n. In this question, base case for n=0 and 1 was enough. Although its not
wrong to prove the base case for 0, 1, 2, 3, 4, 5 when you need to prove only
for 0 and 1, but you should know which values are needed in the base case.
Problem 4 (3) Zach
For problem 4, the only correct way to do
the problem is by induction. If you tried to unravel the induction, 1
point was deducted. In the induction argument, the correct inductive step was
worth 2 points, and the format of the proof and base case were worth 1.
Problem 5 (3) Tom
The biggest issue with this problem was with people
trying to use induction to prove the claim. Only one person in the class
correctly used induction; everyone else who gave an "inductive proof"
ended up proving the result directly. (See below for an explanation of why
induction was not necessary.) No points were taken off for mistakenly thinking
you were using induction. Nor did you lose any points if you were off-by-one,
and claimed that (k+1)! + 1 through (k+1)! + k were all composite. (The first
may not be: consider 3!+1=7.)
If you said that the claim was false, you did not
receive any credit (because your proof was necessarily wrong). Those of you who
said "now let k -> infinity, and we see that there must be an infinite
sequence of composite numbers, which contradicts the infinitude of primes"
received no credit. Infinity is not a natural number, and you cannot let k ->
infinity.
Some people tried to use the Prime Number Theorem as
follows: "we know by the prime number theorem that the primes get sparser,
thus the distance between consecutive primes must be increasing, so eventually
the distance between two consecutive primes will be greater than k, and we've
got our sequence." This does not work, because the prime number theorem is
a statement about the *average* distribution of primes. Assuming the Goldbach
conjecture is true, there are infinitely many "twin" primes -- two
primes p and p+2 -- which means that the distance between primes is not
increasing (though it _tends_ to increase). There were some correct proofs based
on the prime number theorem, which said that if the claim were false (that is,
there existed some k such that there was no sequence of k composite numbers)
then we could establish a minimum on the density of primes (1/k, in fact). Since
we know that the primes *tend* to get sparser [with their density approximately
ln(n)/n], there can be no constant minimum on their density. (You needed more
justification; this is a sketch.)
For those of you who used induction, in [almost] every
case it was unnecessary. The following is a proof:
For any k, let n = (k+1)! + 1. Then [prove this
directly] n+1, n+2, ..., n+k is a sequence of k consecutive composite numbers.
You don't need to wrap this in an induction, with base
cases, a conclusion, etc. Induction is used when the truth of the statement for
one number -- P(n+1) -- follows from the truth of the statement for the previous
number, P(n) [or in the case of strong induction, from the truth of the
statements for ALL previous numbers, P(1) and P(2) and ... and P(n)]. If you can
prove the statement directly (for example, by giving an explicit sequence of k
composite numbers), then induction won't help you. Your inductions were not
*wrong*, exactly; you could prove P(n+1) directly without appealing to P(n), but
that doesn't inherently make it wrong. Using induction where you don't need to
just makes your proof harder to write, understand, and grade.
Problem 6
Problem 7
Common Mistakes
in Problem Set FIVE
Problem 1 (4) Yogi
Most of the students got the idea behind
the question right and they even gave the correct answer that three consecutive
terms are needed to determine the whole sequence, but there were a lot of small
mistakes regarding some degenerate cases (see below). You gathered one point for
the correct answer without any justification (or wrong justifications).
Most of the students got the equation
a(x_n-x_{n+1})=(x_{n+1}-x_{n+2}) (mod p) and then said that we can solve this
equation "easily". You should have said that the we multiply both
sides by the inverse of (x_n-x_{n+1}) (mod p) and then get the value of a. May
be that step was obvious to the students, but this step should be mentioned
because if you mention this, you will catch some mistakes (one of them described
below).
In the above equation, we can not solve for
a if x_n\equiv x_{n+1} (mod p) and then the method of solving fails. (if you
would have said that we multiply by inverse of (x_n-x_{n+1}), then you might
have caught your own mistake by observing that inverse of zero does not exist)
In such a case, we note that x_n=x_{n+1} and then all the subsequent terms are
equal. (see the solution for details). You lost one point if you did not mention
what happens in case of x_n being congruent to x_{n+1} modulo p.
A very few students tried to show that we
cannot determine the whole sequence given just two terms. Some of them tried to
do by giving two terms and showing that two different pairs (a,b) and (a',b')
satisfy x_{n+1}=a(x_{n})+b (mod p) and hence the term x_{n+2} cannot determine
uniquely. This was a nice solution by counterexample. For a more general
solution, see the solutions to this problem set on CMS.
Problem 2 (2+2) Kevin
(a) The most common mistake students made was to count
only powers of p as being not coprime with p^k. Many people forgot to consider
multiples of p that weren't powers of p, like 2p, 3p, etc. Another common
mistake was to overcount p^k, i.e., students would say "there are p^(k-1)
numbers between 1 and p^k that share a factor with p^k, and we don't count p^k
itself, so the answer is p^k - p^(k-1) - 1." This double-counts p^k,
because it is included in the p^(k-1) numbers that share a factor, so you don't
need to subtract it again.
(b) The exact same types of mistakes were made in part
(b) as were made in part (a). Some students did not mention that 2p, 2q, 3p, 3q,
etc. are all not coprime with pq, and consequently they found answers like pq-1,
pq-2, or pq-3. Many people overcounted as in part (a), and were off by plus or
minus 1 (like counting pq twice).
Problem 3 (4) Sam
Most got this question correct using strong
induction. The biggest mistake was trying to prove the claim directly and not
doing so rigorously. It is possible to prove it directly by bounding the number
of operations per bit in the (binary) representation of the input, and showing
that the number of bits decreased in recursive calls. Finally, invoke the well
ordered principle, claiming that the running time is as claimed. However, few
students who tried to prove it directly do so in this fashion. Most just gave an
intuitive reason why the running time was as claimed, or tried to do a worst
case input analysis. The problem with the latter option is that you have to
prove that your worst case really *is* the worst case for this problem, and this
brings you right back to where you started.
Problem 4 (4) Hari
Most people got this problem right. Since
the running time was not required, we didn't take off points for not giving it.
However, students should read the solutions and make sure that they understand
how to give a running time analysis.
The solution just asserts that the running
time of Euclid's algorithm is polynomially bounded. For rest of the argument,
observe that for each number n, we need to compute its gcd with atmost n-1 other
numbers. This way, we do just O(n^2) gcd computations, and hence total time
being polynomial * O(n^2) which is again a polynomial. Once, we get the factors
of the number, finding decryption is O(n) (constant time for each number).
Problem 5 (2) Tom
Almost everyone realized that the solution was p=floor(square
root of n). Problems came up with the running time, though. You needed an
algorithm that was polynomial in the representation of n -- that is, polynomial
in log(n). Assuming that square root took constant time didn't lose you any
points, as a binary search can find sqrt(n) in O(log n) time. If you used the
quadratic formula to get -1 + sqrt(1+n), note that the algorithm does not have
to go through the quadratic formula. It just needs to compute -1 + sqrt(1+n),
which is O(log(n)). (Note that even if you claimed that it is O(1), which is
false, no credit was lost. As long as your algorithm really was polynomial in
log(n), I ignored incorrect analyses.)
The following did lose credit: "[calculations] Now
we know that p is less than sqrt(n), so we just check all the numbers less than
sqrt(n) until we find some k such that (k)(k+2)=n, and then return k and k+2.
This runs in O(sqrt(n)) time." Since every composite number n has a proper
factor less than sqrt(n), this algorithm could be used to factor any number,
even if twin primes weren't used. It is a fact that
O(sqrt(n)) grows faster than any polynomial in log(n)
[ex. log(n)^3+7log(n)^2],
which is why this running time doesn't satisfy the
requirements given in the problem. Note that if you said "We only have to
check a finite number of numbers around sqrt(n), so it's O(log(n))", you
were correct. It's all right to check ANY finite number of numbers, as long as
that finite number doesn't depend on n.
Problem 6 (4) Joel
There were two common forms of mistakes on this problem.
First, people sometimes failed to justify their steps in proving m^(de) = m mod
n. It is necessary (for most proofs) to mention Fermat's little theorem, and
ideally the Chinese remainder theorem. If too many steps were unclear of left
unjustified points were deducted.
A second form of mistake was to misinterpret what the
problem was asking. It was not asking to show that a d exists such that de = 1
mod (p-1)(q-1)(r-1). This follows directly from the assumption that gcd(e,
(p-1)(q-1)(r-1)) exists. Rather it was necessary to show that for d, the inverse
of e mod (p-1)(q-1)(r-1), m^(ed)=m mod n, where n = pqr.
Problem 7 (Optional 0/1) Sam, Yogi
This problem was relatively easier than the
optional problem of the other problem sets. Almost everybody who attempted got
it right. You had to expand (p-1)(q-1) to pq-(p+q)+1 = n-(p+q)+1 and then you
have p+q and pq. Solving the quadratic equation gives the solution. The only
tricky step was to note that solution of quadratic can be found in polynomial
time (especially because the solution, that is the prime number, was an
integer). A couple of students even mentioned that the running time of finding
square root is O(log n) (which is true if we assume multiplication to be
constant time).
A few (many be one or two) students tried
finding the squareroot iteratively (that is starting from one and going up to
the square root). This takes exponential time in the length of the input and is
not correct (as the question asked for a polynomial time algorithm).
Common Mistakes
in Prelim ONE
Problem 1 (Hari)
Most people got this correct but gave
somewhat awkward answers (especially to part a). In general answers of this sort
should be given is easy to read English (see solutions).
Problem 2 (Kevin)
There were many different types of mistakes that were
made by multiple students:
- Some tried to quantify over the variable S, i.e.,
"For all S, ..." or "There exists an S such that...".
This was incorrect. You are given a set S and you must talk about some
property of it.
- Some confused the or-symbol "v" with the
and-symbol "^". I trust people meant to write "or" but
simply transposed the two symbols' meanings in their heads during the
test.
- Many students forgot to specify a domain for their
variables. In other words, many people wrote "There exists an x
such that for all y, there exists an z such that...." without
specifying that x, y, and z are all be members of the set S.
- Some people mixed up the order of the players'
turns. For example, some people wrote "There exists an x such that
there exists a z such that for all y, ...". This is wrong, because it
allows the second player to essentially choose his move after the first
player has committed to both his first and second move.
- A lot of students wrote some form of the
following: "There exists and x in S such that Player 1 chooses x and
for all y in S Player 2 chooses y and there exists a z in S such that
Player 1 chooses z and...." This is wrong: the fact that there exists
a fast win for Player 1 in set S is entirely independent upon whether or
not some instance of the game follows that pattern. If a player
doesn't choose the winning strategy, it doesn't mean the winning strategy
was never a possibility.
Problem 3 (Yogi)
The general statistics on this problem: a
good majority of people got full credit in this problem (or 5.5) and those who
were afraid of using induction, had some problem.
Out of two points on first part, One point
was deducted if you tried calculating a_2, a_3, a_4 but made some algebraic
error (and if you made the error in computing a_2 or a_3, you probably did in
a_4 too). For part (b), figuring out what to do and proving base case of
induction carried 1 point. Doing the correct substitution amounted to 2 points
and manipulating the substituted sum (and hence getting the answer) helped you
get one more point (hence summing to 4 points).
-
Most common mistake was to mess up in
substituting the values of a_1, a_2,... in the sum correctly. For a_i, some
students wrote 2^{n-1}/n instead of 2^{i-1}/i.
-
Some of the students substituted values
of a_1, a_2,... correctly but did not manipulate the sum correctly, making
mistakes in summing the series 1+2+...+2^{k}. They wrote the answer to be
(2^{k+1}-1)/(k-2) while the denominator was supposed to be (2-1). If you
made this mistake, the resulting term was hard to manipulate and you did not
reach the final term.
-
A couple of guys wrote two answers, one
of which was wrong and other correct. You should have crossed out the first
(wrong) part as instructed in prelim.
Problem 4 (Tom)
The mistakes on this problem were of two
kinds: you made a mistake in your arithmetic, or you didn't know how to use
Euclid's algorithm to express gcd(n,m) as a linear combination of n and m (the
second part of the problem). Also some people copied down the numbers n and m
incorrectly.
Problem 5 (Hari)
Lots of people left out a step or two. In general people
seemed to be pretty good with this, though some proofs were hard to read.
A decent number of people got confused with the symbols.
a | b means "a divides b." Unfortunately, if you read it as "b
divides a" the claim is trivially false, so it was difficult to give
partial credit for counter-examples.
Problem 6 (Tom)
Again, here you needed to find the inverse
of 23 mod 101, most likely using Euclid's algorithm. People made mistakes in
arithmetic here as well. Note that 23 * 22 = 506, so it was easy to check if the
inverse you found really was an inverse. While it was theoretically possible to
find the inverse either by brute force (checking every number) or a clever trick
(manipulating equations), only one person actually succeeded in doing this.
Euclid's algorithm was the best method of approaching this problem. A few people
came up with the original answer of 23^99, since for p prime we have a^{p-1} = 1
mod p, showing the inverse of a to be congruent to a^{p-2}. Bear in mind that
this solution only worked because we asked for any integer satisfying the
equation; if we had asked for a number less than 101, this method could not be
adapted to answer the question.
Problem 7 (Sam)
The only problems that were encountered was
confusing relatively prime with congruent to 1 mod m and not explaining why the
induction hypothesis can be used in making the conclusion. In order to get full
credit, it was necessary to mention or show that one step of Euclid's algorithm
is being used.
Problem 8 (Zach)
-
In order to receive full credit for
this part, you needed to have used Fermat's little Theorem (or prove the
statement of it without mentioning its name).
-
For this part, it is not enough to
solve for a in terms of x, as x is an indeterminant. If you did this,
you received only 1 point. It was also not sufficient to give only one
example of an a that worked.
-
This problem was all or nothing.
In order to receive two points, you needed to say that there was one
solution and justify the claim.
Problem 9 (Eva)
Common Mistakes
in Problem Set SIX
Problem 1 (Tom) [4 points]
Problem 2 (John) [3 points]
Problem 3 (Yogi) [4 points]
Most of the students got this problem
right, and those who did not got almost no credit. A very few students were
there who made some small mistakes and hence got only a partial credit.
-
One mistake that many students made
(and I did not take off points for that) is that they did not explicitly
mention that {n \choose -1} is zero or {n \choose n+1} is zero. The best
thing was to drop the term corresponding to k=0 in the summation (as it had
multiplication with k), otherwise, the cases of choosing negative number of
items should have been handled correctly.
-
Some students did the proof by
induction, and
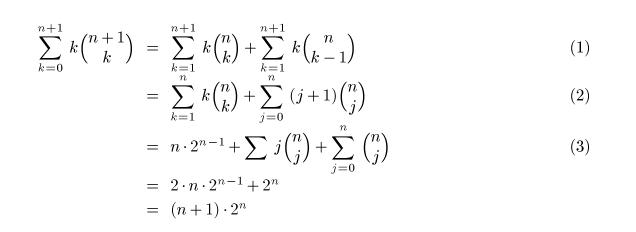
were not comfortable with the step 2 where we substitute k-1=j. If you went
only will step 1 above, you collected 2 points (out of 4 possible).
Problem 4 (Tom) [3 points]
Problem 5 (Kevin) [4 points]
Problem 6 (Joel) [4 points]
Problem 7 (Yogi) [Optional 0/1]
This was a difficult problem compared to
the last problem sets' optional problem. There were three parts to the problem,
and computing s(n,k) was the most difficult. Unfortunately, due to the grading
scheme on optional question, if you attempted two easy parts but did not find
the expresion for s(n,k), you did not get the credit. Some common pitfalls were
the following:
-
Some students said that they found the
particular formula with ``brute force'' and wrote that as their answer. You
were needed to supply the proof/argument how you got the particular
expression for s(n,k), failing which you did not receive any credit (even if
your expression happened to be correct).
-
Some student made the mistake that they
said that we can select n-2k position in just n-2k+1 ways because they could
either be all one, or all zero or 1's followed by zeros. This is true if you
are not allowed to break up this set of n-2k positions. But these n-2k
position could have been divided in k+1 continuous chunks, and hence the
above argument works for each of those chunks, but not for all n-2k
positions. We have to take care of number of ways in which n-2k position can
be partitioned in k+1 parts.
-
Please see the solutions for further
details.