Answers to Review Questions for
the Final Exam

CS 280 - Fall 2002

The Final Exam takes place at noon on Thursday, Dec 12, in Olin 155. I will try to arrive early so that we can start right at noon. Although the final exam will be somewhat longer than the two prelims, I do not expect that you will need the entire 2.5 hours allotted by the registrar for the final exam. I plan to stop the exam and collect the papers by 1:30 or 2 at the latest. The final exam is worth 30% of your final grade; the homework is worth 30%; and the two prelims are each worth 20%.

The use of extra material is not permitted during the exam (i.e., no textbook, no notes, no calculator, etc.).

The exam includes material from readings and lecture throughout the semester, although the material covered since Prelim II will be stressed more heavily. See the Schedule for a list of topics covered in lecture and for the corresponding readings. The exam will attempt to gauge your knowledge and understanding of course concepts. You shouldn't need to memorize long proofs given in the text or in class (although you should understand such proofs).

The review questions given here are not meant to exhaust the possible topics for exam questions. Consider reviewing the previous Review Questions, Prelims I and II, the homework assignments, and the appropriate sections of the text.

Most of these questions are from exams given in previous incarnations of cs280.

Please let me know via email (chew@cs.cornell.edu) if you discover mistakes in my solutions. Past experience indicates that I may have made some.

1. Determine which of the following propositions are tautologies. Show why.
  (p -> (not p)) -> (p -> q)
  tautology, use a truth table
  [(p or q) -> r] <-> [(p -> r) or (q -> r)]
  not a tautology (p=T, q=F, r=F)
2. Write down a proposition P over the variables p, q, r such that P is false only when p, q, r have truth values false, true, false or true, false, false, respectively.
  (p or ¬q or r) and (¬p or q or r)
3. Can such a proposition P be constructed using connectives and and or only? If yes, do. Otherwise, show why not.
  No. Every proposition built from and and or is false when all the atoms are false.
1. Let L(x, y) be x loves y, b be Bob, m be Mary. Give English language translations of the following symbolic sentences (do not use variables in the answer).
  (for all x) (there exists y) L(x,y)
  Everybody loves somebody.
  (there exists x) L(x, b) -> L(m, b)
  If somebody loves Bob then Mary loves Bob.
  (for all x) (L(x,m) -> ¬L(b, x))
  Bob does not love anyone who loves Mary.
  L(b,b) -> ¬L(b, m)
  If Bob loves himself then he doesn't love Mary.
2. Which of the following sentences are logically equivalent? In principle, you have to determine equivalence for all 6 pairs of sentences.
  (there exists x)(A(x) -> B(x))
  (there exists x)(A(x) -> (for all y)A(y))
  (for all x)A(x) -> (there exists x)B(x)
  (there exists x)B(x) or (for all y)¬B(y)
  The first is equivalent to the third. The second is equivalent to the fourth (both are equivalent to True).
Which of the following are true (A and B are arbitrary sets)? Yes/No answers. The symbols for set operations are difficult in html, so the notation here is odd.
1. if A subset B and B={Ø} then A=B.
2. if A subset B and B={Ø} then A=Ø.
3. Ø elementOf A
4. Ø subset A
5. (A union B^c)^c = B intersect A^c
6. A intersect B = (A^c union B^c)^c
7. (A - B) intersect (B - A) = Ø
8. if A x B = Ø then A=Ø and B=Ø
9. A subset A x A
10. A x A = A for some A
  d, e, f, g, j are true
1. How many one-to-one functions from {a, b, c, d} onto {1, 2, 3, 4, 5} are there?
  None. To be one-to-one and onto the sets must have the same number of elements.
2. How many one-to-one functions f from {1, 2, 3, 4, 5} onto itself are there such that f = f ^-1?
  This can happen only when items are swapped in pairs. There is one function where none are swapped. There are C(5, 2) where a single pair is swapped. There are C(5, 2) * C(3, 2) / 2 where two pairs are swapped. The solution is the sum of these: 1 + 10 + 15 = 26.
3. Let f be function. Which of the following are true?
  f(A intersect B) = f(A) intersect f(B)
  False. Let A be the interval [0, 1] and B be the interval [2, 3].
  f(A union B) = f(A) union f(B)
  True. Consider y in f(A union B). By definition, there exists an x in A union B such that f(x) = y. Note that x is in A or x is in B. If x is in A then y=f(x) is in f(A). If x is in B then y=f(x) is in f(B). In either case, y is in f(A) union f(B). Consider y in f(A) union f(B). Similar arguments show that y is in f(A union B).
  f ^-1(C intersect D) = f ^-1(C) intersect f ^-1(D)
  True. Consider x in f ^-1(C intersect D). By definition there exists a y in C and in D such that f(x)=y. By definition, f ^-1(C) contains x and f ^-1(D) contains x. Similar arguments show the other direction.
  f ^-1(C union D) = f ^-1(C) union f ^-1(D)
  True. Consider x in f ^-1(C union D). By definition there exists a y in C or in D such that f(x)=y. In either case, x is in f ^-1(C) union f ^-1(D). Other direction is similar.
  f(A) = f(A)
  False.
  f ^-1(C) = f ^-1(C)
  True. x in f ^-1(C) iff f(x) in C iff not(f(x) in C) iff not(x in f ^-1(C)) iff x in f ^-1(C).
Yes/No answers. Is it true that n² is O(g(n)) if g(n) is
1. 100n² + 101n
2. n³
3. n log n
4. n²log n
5. n² + log n
  True for a, b, d, and e.
1. Use the Euclidean Algorithm to find gcd(111, 2222).
  gcd(111, 2222) = gcd(111, 2) = gcd(1, 2) = 1
2. Find the inverse of 6 modulo 11.
  2
3. Find a positive integer x such that x = 3(mod 9) and x = 5(mod 10).
  75
1. Determine which of the following propositions are tautologies. Show why.
  (p → ¬q) → ( ¬q → p)
  Not a tautology. Consider p and q both false.
  [(p or q) → r] ↔ [(p → r) and (q → r)]
  Tautology. Can show by manipulating propositions or by truth table.
2. Write down a proposition P over the variables p, q, and r such that P is true only when p, q, r have truth values FFT or TFT.
  ( ¬p and ¬q and r) or (p and ¬q and r). This is equivalent to ( ¬q and r).
3. Can such a P be constructed using the connectives and and → only (no truth constants for T and F are allowed)? If yes, do so. Otherwise show why not.
  No. Note that P is false when p, q, and r are all true. But any combination of and and → is always true.
1. Let L(x, y) be x loves y. Write the following as formal sentences with quantifiers.
  Everybody loves somebody. (for all x)(there exists y)L(x, y)
  Everybody loves everybody. (for all x)(for all y) L(x, y)
  Somebody loves everyone. (there exists x)(for all y) L(x, y)
  Somebody loves someone. (there exists x)(there exists y) L(x, y)
2. Which of the following sentences are logically equivalent (answer only)? In principle you have to determine the equivalence of all 6 pairs of sentences. Assume B does not contain x.
  (for all x)(A(x) →B),
  (for all x)A(x) →B,
  (there exists x)(A(x) →B),
  (there exists x)A(x) →B.
  The middle two are equivalent and the first is equivalent to the last. Here's a proof for the first and last: (for all x)(A(x) →B)
  <=> (for all x) [ ¬A(x) or B]   by def of →
  <=> (for all x) [¬A(x)] or B    by cases (B true or B false)
  <=> [¬(there exists x) A(x)] or B   by negation of quantifiers
  <=> (there exists x) A(x) → B   by def of →
Which of the following are always true (A, B, C are arbitrary sets)? Yes/No answers.
if A subset B and B subset A then A = B
1. if A subset B and B subset A then A = B
  True
2. Ø elementOf {Ø}
  True
3. Ø elementOf A
  False
4. Ø subset A
  True
5. if A != B and B != C then A != C
  False
6. A-B = (A^c - B^c)^cFalse (consider A=B)
7. (A - B) intersect (B - A) = Ø
  True
8. Ø x A = Ø
  True
9. A x B = B x A
  False
10. A union B = A union B
  False
How many one-to-one functions f from {1, 2, 3, 4, 5 }onto itself are there such that f ◦f ◦f is the identity function?
We know that f(f(f(x))) = x. This can only happen if f(x)=x or if x is part of a 3-cycle (i.e., x maps to f(x) which maps to f(f(x)) which maps to x and x, f(x), and f(f(x)) are all different). There are only 5 elements, so there is only room for one 3-cycle. How many possible 3 cycles are there? There are C(5, 3) ways to choose 3 element. Once those elements are chosen there are 2 ways to form them into a 3-cycle (i.e., 1→2→3 is different from 1→3→2, but is the same as 2→3→1). So there are 2C(5, 3) = 20 ways to have a 3-cycle; plus we have one more for no 3-cycles. Thus the total number of functions is 21.
Yes-No answers. Is it true that n² is O(g(n)), if g(n) is
n   No
n³    Yes
n log n   No
2ⁿ    Yes
n!   Yes
n²log n    Yes
n² + log n    Yes
n² / log n   No
(n⁴ +1)/(n² +1)    Yes
(n⁴ +1)/(n +1)   Yes
Find 5²⁰⁰⁰¹ (mod 143). The answer should be a standard integer between 0 and 143.
Ideally, we'd like to use Fermat's Little Theorem [ a^p-1 = 1 (mod p) for p prime], but 143 is not prime since 143 = 11*13. Note though that, by Fermat's Little Theorem, 5¹⁰ = 1 (mod 11) and 5¹² = 1 (mod 13). Thus 5²⁰⁰⁰¹ = 5 (mod 11) and 5²⁰⁰⁰¹ = 5⁹ (mod 13). Further, 5² = 25 = 12 = -1 (mod 13), so 5²⁰⁰⁰¹ = 5⁹ = 5(5²)⁴ = 5(-1)⁴ = 5 (mod 13). In other words, 5²⁰⁰⁰¹ - 5 is divisible by both 11 and 13. This implies that 5²⁰⁰⁰¹ - 5 is divisible by 143, so the final answer is 5.
1. Suppose that S(n) is a proposition involving a nonnegative integer n, and suppose that if S(k) is true then so is S(k + 2). Which of the following are possible (answer only)?
  S(n) holds for all n ≥0,   Possible
  S(n) holds for all n ≥1, but S(0) is false,    Possible
  S(n) is false for all n ≥0,    Possible
  S(n) is true for all n ≤100 and false for all n >100,    Not possible
  S(n) is false for all n ≤100 and true for all n >100.   Possible
2. A collection S of strings of characters is defined recursively by (1) the empty string is in S and (2) if X belongs to S then so does aXb. Which of the following belong to S (Yes-No answers):
  a     No
  b      No
  c      No
  ab      Yes
  abb      No
  aabb     Yes
1. A questionnaire is sent to 13 freshmen, 5 sophomores, 15 juniors, and 20 seniors. A student won’t necessarily return his/her questionnaire. How many questionnaires must be received to ensure getting 9 from the same class?
  We can receive 8 from freshmen, 5 from sophomores, 8 from juniors, and 8 from seniors without getting 9 from any one group. If we get one more, we have have at least 9 from some group so the answer is 8+5+8+8+1 = 30.
2. How many bit strings are there of length 10 with two or more 1’s in the string?
  There are 2¹⁰ bit strings. Of these 1 has no ones and 10 have exactly one 1. So the answer is 1024 - 10 -1 = 1013.
1. Find the number of positive integer solutions of x + y + z ≤100.
  We use a standard trick to convert this inequality into an equality: introduce a new variable w. The problem becomes: Find the number of solutions to w + x + y + z ≤ 100 subject to the constraints that w>0 and x, y, and z are > 1. Consider w, x, y, and z as bins. Bins x, y, and z each start out holding one star. We now have 97 stars to distribute into 4 bins (i.e., 3 bars). Thus the answer is C(100, 3).
2. A hostess wishes to invite 6 dinner guests. In how many ways can she place them on 6 distinguished seats?
  6! = 720
3. The same question for a round table with indistinguishable seats.
  We place one guest. Now there are 5! = 120 ways to place the remaining guests.
Two fair dice are rolled. What is the probability that
1. the number on the first die is strictly less than the number on the second die?
  15/36 = 5/12.
2. one of those numbers is strictly less than the other one?
  This is always true except when doubles are rolled. Answer: 30/36 = 5/6.
3. the product of those numbers is even given that their sum equals 6?
  There are 5 ways for the sum to be 6 [(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)]. Of these 2 have an even product. The answer is 2/5.
A couple agrees to keep having children until they have at least one boy and one girl, but not more than 5 children. Assume that boys and girls are equiprobable and that the births are mutually independent. What is the expected value and variance of the number of
1. children ?
  Let X be the random variable representing the number of children. We can list all the patterns that can occur: BG, GB, BBG, GGB, BBBG, GGGB, BBBBG, GGGGB, GGGGG, BBBBB. The probability for each pattern is 1/2ⁱ where i is the length of the pattern. So E(X) = 2(1/4 + 1/4) + 3(1/8 + 1/8) + 4(1/16 + 1/16) + 5(1/32 + 1/32 + 1/32 + 1/32) = 1/8[8 + 6 + 4 + 5] = 23/8.
  E(X²) = 4(4/8) + 9(2/8) + 16(1/8) + 25(1/8) = (16 + 18 + 16 + 25)/8 = 75/8.
  V(X) = E(X²) - E(X)² = 75/8 -(23/8)² = 71/64.
2. girls ?
  Let B and G be the random variables for number of boys and number of girls, respectively. We know that E(X) = E(B+G) = E(B) + E(G). By symmetry E(B) = E(G). Thsu E(G) = 23/16.
  E(G²) = 0²(1/32) + 1²(1/4 + 1/4 + 1/8 + 1/16 + 1/32) + 2²(1/8) + 3²(1/16) + 4²(1/32) + 5²(1/32) = (0 + 23 + 16 + 18 + 16 + 25)/32 = 98/32.
  V(G) = E(G²) - E(G)² = 255/256.
An integer is randomly selected from 1 to 1000. What is the probability that it is divisible by 2 or by 3 or by 5?
Use inclusion/exclusion. Let A be the event "divisible by 2", B be the event "divisible by 3", and C be the event "divisible by 5".
P(A union B union C) = P(A) + P(B) + P(C) - P(A intersect B) - P(A intersect C) - P(B intersect C) + P(A intersect B intersect C) = (500 + 333 + 200 - 166 - 100 - 66 + 33)/1000 = 734/1000.
Give an example of a relation R that is
1. symmetric, not reflexive
  R = {(x, y) | x = -y}
2. reflexive, symmetric, not transitive.
  R = {(x, y) | |x-y| = 1}
1. How many vertices and edges does the graph Q₅ have?
  The number of vertices doubles each time the dimension increases, so there are 2⁵ = 32 vertices. Each vertex has degree 5, so the number of edges is 32*5/2 = 80.
2. A graph has 7 vertices, 3 of them of degree two and 4 of degree one. Is this graph connected? Why?
  No. We can count the number of edges: (6 + 4) / 2 = 5. A tree on 7 vertices has 6 edges, so the graph cannot have spanning tree and thus it cannot be connected.
Which of the following graphs are planar? (Answer only)
K₅     Not planar
Q₃     Planar
K_2,5     Planar
K_3,5     Not planar
K_4,5     Not planar
1. Suppose that S(n) is a proposition involving a nonnegative integer n, and that if S(k) is false for all k<n then so is S(n). Which of the following are possible (answers only).
  S(n) is false for all n.     Possible
  There is an integer M > 0 such that S(n) is true for all n < M and false for all n > M.     Impossible due to S(0). The problem statement requires S(0) to be false.
  S(n) is true for all n.     Impossible due to S(0)
  There is an integer M > 0 such that S(n) is false for all n < M and true for all n > M.   Impossible
2. A collection S of strings of characters is defined recursively by (1) a belongs to S and (2) if Xa belongs to S then so do Xaa and Xb. Which of the following belong to S?
  b
  aa
  ab
  abb All belong except this one.
  aab
1. How many students must be in a class to guarantee at least k students with the same birthday in the year 2000? Answer for k=1, k=2, and k=3.
  The year 2000 has 366 days (it's a Leap Year). Answers are 1, 367, and 733, resepctively.
2. A multiple choice exam has 20 questions, each with 5 possible answers, and 7 additional questions, each with 3 possible answers. How many different answer sheets are possible?
  5²⁰3⁷.
1. In how many ways can a committee of 3 mathematicians and 5 computer scientists be selected from a panel of 20 having 10 mathematicians and 12 computer scientists?
  The panel must have 2 people who are both mathematicians and computer scientists. Of the remainder 8 are mathematicians only and 10 are computer scientists only. The committee can include both of the two dual-career people, one of the two dual-career people or none of the two dual-career people. The answer is
  C(8, 1) C(10, 3) + 2 C(8, 2) C(10, 4) + C(8, 3) C(10, 5).
2. Find the number of positive integer solutions of x + y < 100.
  We convert this to w + x + y = 100 where w > 0, x > 0 , and y > 0. Thus, we have 98 items to place into 3 bins (i.e., two bars). The answer is C(100, 2) = 4950.
1. Find the probability that a family with six children has a boy and a girl (sexes of children are assumed equiprobable and independent).
  There are 2⁶= 64 possible ways to have a family of 6 children. Of these there are just 2 ways to avoid having both a girl and a boy. Answer: 62/64 = 31/32.
2. What is the most likely number of boys?
  Let B be the random variable for the number of boys.
  E(B) = 0(1/64) + 1(6/64) + 2(C(6, 2)/64) + 3(C(6, 3)/64) + 4(C(6, 4)/64) + 5(C(6, 5)/64) + 6(1/64)
  = (6 + 30 + 60 + 60 + 30 + 6)/64 = 192/64 = 3.
  Alternately, let G be the random variable for the number of girls. We know 6 = E(B+G) = E(B) + E(G). By symmetry E(G) = E(B) = 3.
3. Find the probability of having at least one girl given the first three children are boys.
  Let A be the event "at least one girl" and let B be the event "the first 3 are boys". We want to find P(A|B) = P(A intersect B) / P(B) = [(3 + 3 + 1)/64] / [8/64] = 7/8.
A fair die is rolled until the sum of the spots exceeds 2. What is the expected number of rolls?
The only way to use 3 rolls is to roll 1, 1, and then anything.
Two rolls are used by 1, anything>1.
Two rolls are used by 2, anything.
One roll is used by anything>2.
Expected number of rolls = 3(1/6)(1/6) + 2(1/6)(5/6) + 2(1/6) + 1(4/6) = (3 + 10 + 12 + 24)/36 = 49/36.
An integer is randomly selected from 1 to 100. What is the probability that it is divisible by 2 or by 3, but not by 5?
Let A be the event "is divisible by 2", B be the event "is divisible by 3", and C be the event "is divisible by 5". Observe that the event we want is (A union B union C) - C and that C is a subset of (A union B union C). Thus we want P(A union B union C) - P(C).
P(A union B union C) - P(C) = P(A) + P(B) - P(A intersect B) - P(A intersect C) - P(B intersect C) + P(A intersect B intersect C)
= (50 + 33 - 16 - 10 - 6 + 3)/100 = 54/100.
Give an example of a relation on {a, b, c} which is
1. reflexive, not symmetric
  The standard < works here.
2. irreflexive, symmetric
  The not-equal relation works here.
3. reflexive, symmetric, not transitive
  R = {(a, a), (b, b), (c, c), (a, b), (b, a), (b, c), (c, b)}
1. Reorder the words in this phrase lexicographically.
  in, lexicographically, phrase, Reorder, the this, words
2. Find the smallest possible poset having exactly two minimal elements and exactly three maximal elements. Does it have a greatest element and a least element (answers only)?
  Use {a, b, c, d} where d<b and d<c. This results in a, b, and c maximal, while a and d are minimal. There is no greatest elements or least element.
1. Indicate all possible vertex degrees occurring in the following graphs: K₃, C₁₇, K_3,5, Q₄.
  2, 2, (3, 5), 4
2. Is there a simple graph with exactly 3 vertices of degree 3?
  Yes (there have to be some other vertices of odd degree as well).
3. Is there a simple graph with 10 vertices and 46 edges?
  No. The complete graph on 10 vertices has C(10, 2) = 45 edges.
4. Is there a connected graph with 100 vertices, 96 of them of degree two and 4 of degree one?
  No. Such a graph would have [(2*96) + 4 ] / 2 = 98 edges. A spanning tree on 100 vertices needs 99 edges, so such a graph cannot be connected.
Which of the graphs in 30a are planar (answers only)?
planar, planar, not planar, not planar
Consider the following graph.
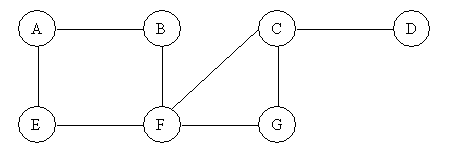
Draw the Breadth-First-Search (BFS) tree for this graph. Whenever there is a choice of vertices, choose the one earliest in the alphabet.
```
    A
   / \
  B   E
  |
  F
 /  \
C    G
|
D
```
Consider the following digraph.
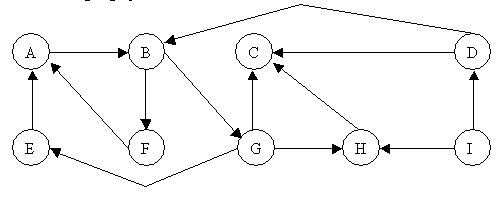
Which vertices are in the same weakly connected component as A? All are.
Which vertices are in the same strongly connected component as A? A,B,E,F,G.
Draw the Breadth-First-Search (BFS) forest for this graph. Whenever there is a choice of vertices, choose the one earliest in the alphabet.
```
    A       D      I
    |
    B
   / \
  F   G
     /|\
    C E H
```
Which of the following statements are true for any sets A and B. B^c represents the complement of B.
1. A subset (A union B) - B
2. A - B = A intersect B^c
3. (A intersect B) union B = A
4. Ø subset A intersect B
5. A = A union {Ø}
  b, d are true.
An instructor gives an exam with 8 questions. The students are told to choose any 6 of the questions to answer (i.e., each student is instructed to skip two questions, student's choice). When the tests are graded, the instructor observes: (1) No two students chose to answer the same set of 6 questions. (2) If the class had just one more student then it would not have been possible for (1) to hold.
1. How many students are in the class?
  There are C(8,6) = 28 ways to choose the 6 out of 8 questions. So there are 28 students in the class.
2. A student taking the exam has 50 minutes to spend on 6 questions. How many different ways are there to distribute the 50 minutes among the 6 questions? The questions are distinguishable (i.e., the pattern (45, 1, 1, 1, 1, 1) is considered to be different from the pattern (1, 1, 1, 1, 1, 45)). Assume that each minute is devoted to a single question (i.e., no partial minutes) and that each question requires a minimum of 1 minute. Assume the student uses all 50 of the minutes.
  We have 50 items to place into 6 bins. Each bin must contain 1 item. After distributing one item to each bin, we are left with 44 remaining items to place into 6 bins. Thus we have 44 stars and 5 bars, so the solution is C(49, 5).
3. How many different ways are there if the student doesn't necessarily use all 50 minutes?
  This just introduces a new bin where the extra minutes are placed. We now have 50 items to place into 7 bins; 6 of the bins must hold at least one item. In other words, we have 44 items to place into 7 bins; 44 stars and 6 bars. The solution is C(50, 5).
Consider the number 107¹⁰⁷. What is the second digit from the right when this number is written in standard number notation? (Example: The second digit from the right in the number 9988776654321 is 2.)
To get the second digit, we work (mod 100). 107¹⁰⁷ = 7¹⁰⁷ (mod 100). Now we need to know about powers of 7. 7² is 49, 7³ is 343=43, 7⁴ is 301=1 (all mod 100). So we know we can take the exponent (mod 4) to get the final answer: 7¹⁰⁷ = 7³ = 43 (mod 100). The second digit is 4.
1. A string is built using the following steps, in order. Whenever there is a choice, each choice is equally likely. (1) Randomly choose an element from {T, F}. (2) Randomly choose an element from {and, or, implies}. (3) Randomly choose an element from {T, F}. The resulting string is a (trivial) logical proposition. What is the probability that this proposition evaluates to True?
  There are 2*3*2 = 12 possible strings. Of these, the ones that are True are (T and T), (T or T), (T or F), (F or T), (T implies T), (F implies T), and (F implies F). So the probability is 7/12.
2. A string is built using the following steps, in order. Whenever there is a choice, each choice is equally likely. (1) Randomly choose an element from {p, not p, T, F}. (2) Randomly choose an element from {and, or, implies}. (3) Randomly choose an element from {p, not p}. The resulting string is a logical proposition. What is the probability that this proposition is a tautology?
  This time there are 4*3*2 = 24 possible strings. Of these, the ones that are tautologies (i.e., always true) are (T or p), (T or not p), (p or not p), (not p or p), (F implies p), (F implies not p), (p implies p), and (not p implies not p). So the probability is 8/24 = 1/3.
Consider a simple dice game involving a pair of dice. When the dice are rolled, the player wins if 7 is rolled or if doubles (i.e., both dice show the same number) are rolled.
1. If the game is played 100 times, what is the expected value and variance of the number of wins?
  This is a Bernoulli trial problem. The probability of success is p = (6+6)/36 = 1/3. For n Bernoulli trials the expectation is np = 100*(1/3) = 100/3. The variance is npq = (100)(1/3)(2/3) = 200/9.
2. Suppose the game as stopped as soon as either (1) the player wins or (2) the dice are rolled 3 times. What is the expected number of dice rolls?
  Let X be the number of rolls.
  p(X=1) = 1/3 = 3/9.
  p(X=2) = (2/3)*(1/3) = 2/9.
  p(X=3) = (2/3)*(2/3) = 4/9.
  E(X) = (3/9)(1) + (2/9)(2) + (4/9)(3) = (3+4+12)/9 = 19/9.

Answers to Review Questions for the Final Exam

CS 280 - Fall 2002

Answers to Review Questions for
the Final Exam