Streaming Pies

Remember Taylor Series from Calculus? One important application of Taylor Series is that we can use them to calculate approximations of transcendental numbers like and e. For instance, can be defined to be the sum of the infinite series:

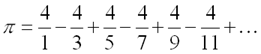
To approximate , we simply chop off the tail of the series at some point and add up all the fractions.

In the problems below, you will build a Scheme representation of as a stream of rational numbers using only the rational and stream-processing functions defined below, together with cons-stream, heads, and tails. In particular, none of the code you write should include lambda or letrec. Unfortunately, whoever wrote this code had no idea how to choose identifiers so he or she made your job really hard.

(define (nats-from <function>)
  (lambda ((n <integer>))
    (cons-stream n (nats-from (+ n 1)))))

(define (f <function>)
  (lambda ((s <stream>))
    (cons-stream (heads s) (f (tails (tails s))))))

(define (g <function>)
  (lambda ((s1 <stream>) (s2 <stream>))
    (cons-stream (heads s1) (g s2 (tails s1)))))

(define (h <function>)
  (lambda ((f <function>) (s1 <stream>) (s2 <stream>))
    (cons-stream (f (heads s1) (heads s2))
                 (h f (tails s1) (tails s2)))))

(define (k <function>)
  (lambda ((f <function>) (s <stream>))
    (cons-stream (f (heads s)) (k f (tails s)))))

Recall that <rational> is a Scheme primitive class with accessors numerator and denominator.

Fortunately, we're going to walk you through it...

1. Define an infinite stream of all 4's (i.e., [4, 4, 4,...]).

   (define fours

   
   
   
   
   
2. Define an infinite stream of the odd naturals (i.e., [1, 3, 5, 7, 9, 11,...]).

   (define odd-naturals

   
   
   
   
   
3. Define an infinite stream of the odd naturals where every other number is negated (i.e., [1, -3, 5, -7, 9, -11,...]).

   (define denoms

   
   
   
   
   
4. Define the stream of rationals whose sum is (i.e., []).

   (define pi

   
   
   
   
   

Solution

Return to CS 212 Final - Spring 1998