CS212Problem Sets
CS212Problem Sets
This problem set is even more difficult than the last one. Even though it probably looks short, it's not. You'll need serious time to think before even beginning to code most of these problems. This is not a sit-down-in-one-night-and-crank-it-out problem set; in fact, this isn't a sit-down-in-three-nights-and-crank-it-out problem set. You should start on it early, at the very least to get ideas about the questions floating around in your head. We're warning you...do NOT let this problem set go until the last minute!
In general, the problems are such that a little bit of thought will save you tremendous headaches. You should attempt to write out solutions to each question well before you sit down at the computer.
There has been some confusion, so, to clarify: sample output provided is a sample only. You need to demonstrate that your functions work correctly on a sufficiently wide range of inputs. One of your tasks in this problem set is to decide what needs to be tested and to do so. Show us the output of these tests.
There is quite a bit of code in the ps4.ss file that is not discussed in the text of the problem set. You should be familiar with it.
Last word of advice: filter and map are very, very useful functions, and can be used to make your life so incredibly much easier. Take advantage of that fact.
In this problem set, we will be investigating graphs and automata. A graph consists of two things: a set of points (also called vertices or nodes) and a set of lines connecting those points (called edges). Formally, a graph is an ordered pair G = (V,E) where V is the set of vertices and E is the set of edges.
Each edge is represented by an ordered pair of vertices. Edges can have direction (in which case the graph is called directed) or not (in which case the graph is called undirected). In a directed graph, the edge (u, v) is the edge from u to v and the edge (v, u) (the edge from v to u) is completely distinct. In an undirected graph, however, the edge (v, u) is considered the same as the edge (u, v).
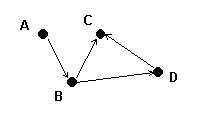This is an example of a directed
graph. The vertices are A, B, C, and D, or in set notation,
V = {A, B, C, D}. The edges are represented as
ordered pairs (pairs in the mathematical, not Scheme, sense): the first
element of the pair is the source (where the edge comes from);
the second is the destination (where the edge goes). So
E = {(A, B), (B, C), (B, D), (D, C)}.
We refer to a path between two vertices u and v as an ordered sequence of edges [(u, u1), (u1, u2), ..., (un, v)]. For example, in the graph shown, there is a path from A to C, namely [(A, B), (B, C)]. The path [(A, B), (B, D), (D, C)] is also a path from A to C, although it is longer. Often, a path will be abbreviated to the sequence of vertices traveled in that path. So, the path from A to D would be abbreviated into the sequence [A, B, D].
There are two standard ways of representing a graph in memory: an adjacency matrix or an adjacency list. An adjacency matrix keeps a two-dimensional array indexed by the vertices of the graph in both directions. Cell (i, j) contains 1 if and only if there is an edge from vertex i to vertex j in the graph; otherwise it contains 0. An adjacency list, on the other hand, maintains for each vertex a list of vertices adjacent to it.
| A graph | |||||||||||||||||||||||
|
|||||||||||||||||||||||
| As an adjacency matrix | As an adjacency list | ||||||||||||||||||||||
|
|
||||||||||||||||||||||
There are advantages to each representation. For example, attempting to discover whether an edge exists between two vertices u and v is simply a matter of accessing a single cell Adj[u,v] in an array with an adjacency matrix, an O(1) operation. In an adjacency list, however, one must look through the entire list of vertices adjacent to u and see if v appears. There can be as many as V (the total number of vertices in the graph) vertices in the list of vertices adjacent to u, so it could take as much as O(V) time to find whether v is adjacent to u.
The advantage of using adjacency lists is that if we ever need to do anything to all the edges, we can simply walk down the lists for each vertex and do whatever we need to do. This runs in O(E) time (where E is the total number of edges in the graph), while with an adjacency matrix, we need to look at every cell of the array (since we don't know whether there is an edge between two vertices until we check that cell), which is O(V2) time. An easy way to see this is to look at the size of the representation: with an adjacency matrix, there are V2 entries in the array, regardless of the number of edges, while an adjacency list has one element in a list per edge in the graph.
We will implement graphs using something like adjacency lists because the graphs we are dealing with are going to be (generally) sparse graphs, which means that E<<V^2 ("E is much less than V^2"). (Intuitively, the sparcity of a graph directly corresponds to the density of "0"s in an adjacency matrix representation of the graph.) In sparse graphs, the advantages of the adjacency list outweigh its disadvantages greatly. So that's what we'll use.
We have provided three predefined classes in the code, <graph>, <vertex>, and <edge>. The graph type has two slots, both lists: one a list of <vertex>s, the other a list of <edge>s. The vertices contain only names, but the directed-edges contain two vertices, as discussed above.
Two important graph functions have been defined for you. The function find-vertex takes a name of a vertex and a list of vertices, and finds the vertex in the list with the name given. The function returns that <vertex> or #f if no such vertex exists. (Note the function find-in-graph, which is just a shortcut to one of the common uses of find-vertex.)
The function create-graph is a little more complicated. This function takes in a list of symbols (which will become the names of vertices) and a list of (two-element) lists which describe the edges of the graph. The structure of the edge list is as follows:
((U1-source U1-dest) (U2-source U2-dest) (U3-source U3-dest) ... )
where Un-source and Un-dest are the names of the source and destination vertices of the n-th edge (note that order does not matter). The vertices must, of course, be contained in the vertex list. (Although this relation is not actually checked by the function, it easily could have been.) In the actual call to make-graph inside create-graph, map is used in a fairly clever way. You should look over this code, because you will be writing similar functions throughout the problem set.
Using the given graph functions and type definitions, write a function exits which, given a graph and a vertex (as always, be careful about the difference between a vertex--that is, an object of type <vertex>--and the name of a vertex) in the graph, returns a list of vertices that can be reached from the vertex by following a single edge in the graph. (This function will be very useful for later problems.)
Also implement a predicate is-edge? which, given a graph and two vertices in the graph, returns #t just in case there is an edge from the first vertex to the second in the given graph. (Note that this function is trivial once you've completed the first part of this exercise.)
Following standard conventions, is-edge? returns a boolean (that is, strictly #t or #f). If we asked you for is-edge, it would be acceptable to have it return any non-false value if an edge exists. For example, consider member.
Let us define a path in a graph: a path from vertex u to vertex v in graph G is a (non-empty) list of vertices in G connected by edges, starting with u and ending with v. (Note that a path from a vertex to itself does not necessarily exist.)
Write a function verify-path, which takes a graph and a list of vertices, and verifies that the list is indeed a valid path (from the first element in the list to the last element in the list) in the given graph.
Sample Output:
==> (define g1 (create-graph '(a b c d e)
'((a b) (a c) (b c) (b e) (c d) (d b))))
==> (display-vertices (exits (find-in-graph 'b g1) g1))
(c e)
==> (is-edge? (find-in-graph 'a g1) (find-in-graph 'b g1) g1)
#t
==> (is-edge? (find-in-graph 'c g1) (find-in-graph 'a g1) g1)
#f
==> (verify-path (map (lambda (x) (find-in-graph x g1))
'(a b c d b e))
g1)
#t
==> (verify-path (map (lambda (x) (find-in-graph x g1)) '()) g1)
#f
==> (verify-path (map (lambda (x) (find-in-graph x g1)) '(a d b)) g1)
#f
What to turn in: Turn in your definitions of exits, is-edge? and verify-path, and output showing the functions working.
A DFA (deterministic finite automaton (plural: automata)) is a directed graph in which the edges are labeled, i.e. each edge has a name associated with it. The set of possible symbols (in the non-scheme sense) that can be in labels is called the alphabet of the automaton. In a finite automaton, vertices are called states. The function of an automaton is to scan an input sequence one symbol at a time, and decide whether to "accept" the sequence or not. These theoretical machines are useful in pattern matching (regular expressions) and compilers. They are also used all the time (in slightly modified form) in hardware.
You can think of a DFA as a kind of map (a road map, that is, not the function map). The states of the automaton are towns, and the edges are one-way roads going between them. One state is the starting point, called the start state. Any number of states (including possibly the start state) are designated as final states. The "goal" is to traverse (travel along) the roads, starting at the start state and ending at one of the final states.
Note that in the following few paragraphs, we use "character" to refer to a member of the automaton's alphabet, not a data type.
To do this, you are given a sequence, which we will represent by an ordered list of characters. Think of these as tokens in a Pez dispenser (or elements on a stack, if you're too young to remember Pez). You need the tokens to pay a toll on the road, and different toll booths require different tokens. It's like a Pez dispenser (or stack) because you can only use the first token you have (the top of the stack), and you can't take it out of the dispenser (off the stack) unless you use it (pop the stack).
So use the input symbols one at a time, removing the first one whenever a transition labeled with that character is traversed (you pay the toll). If at any time there is no transition that can be traversed, you "lose" the game (since you're stuck and can't move anywhere). If this does not happen, when you run out of characters, you "win" if and only if you are in a final state. Sequences of characters which make you "win" represent "accepted" sequences, and those that make you "lose" are "rejected". The usefulness of DFAs comes from the types of sequences that they accept.
The D in DFA stands for deterministic. This means that whenever you move in the automaton, you have no choices. You are either forced along one route by the character at the front of the remaining sequence, or you're stuck and the sequence is rejected. (That is, there is at most one transition with a given symbol from each state.)
Formally, a DFA is a collection of 5 things:
| Q | the set of states, which we will implement as a list of <object>s. This is analogous to V in a generic graph. |
| Sigma | the alphabet, a list. Remember, this is the collection of possible transition labels (token types). The alphabet can be made up of <symbol>s or <number>s, as you will see below, so this will be a list of <primitive>s. |
| F | the set of final states (F is a subset of Q). This specifies which states of the graph are "winning" states. |
| q0 | the start state (q0 is an element of Q). |
| delta | the transition function, which, given a state and an input symbol returns a new state. In other words, this is the function that describes where the edges in the graph go. |
For clarity, in the examples given below we will always denote states by letters and use the fixed alphabet {0, 1}. In the code you write, however, you need to assume that these can be arbitrary.
An NFA (nondeterministic finite automaton) is just like a DFA except for one minor detail. In an NFA, there can be many transitions that apply at any given time. Going along with the Pez dispenser analogy, this means that whenever you stand at an intersection, there could be many roads that require your current Pez as their toll. A traversal through the machine requires you to choose which transition to take when there is more than one possibility.
For an NFA, making bad choices doesn't hurt you. In other words, if there exists any "good" choice of traversal, then the machine (automaton) accepts the input, regardless of how many bad choices there are.
In this problem set, we will not address the issue of multiple start states, which are found in standard NFAs.
Define a new class <labeled-edge> as a subclass of <edge>. Give the class a new slot, label, of the appropriate type as described above. Write a function display-labeled-edges, analagous to display-edges.
Now define a new class <automaton> as a subclass of <graph>. Give this class the slots for a start state (of type <vertex>s) and final states (a <list> of vertices).
Hint: Some of our code depends on you implementing this in a certain way, so make sure you are familiar with our code (and how defstruct creates certain functions).
Also define a constructor create-automaton analogous to create-graph.
Here's your first DFA, although you can't do anything yet except create it.
==> (define dfa1
(create-automaton
'(a b c)
'((a a 0) (a b 1) (b a 1) (b c 0) (c b 0) (c c 1))
'a
'(a)))
This DFA (as you will see) accepts binary numbers divisible by 3. You should draw this out on a piece of paper to convince yourself.
What to turn in: Turn in your type and constructor definitions for the types <labeled-edge> and <automaton>, and your definition of display-labeled-edges. You need not turn in output for this part.
Now that we've defined most of the underlying structure for the automata, one thing is still missing: the notion of the delta function, which takes a state and an input symbol and returns a list of destination states. The encoding for this relation is in the labeled edges of the graph.
Define a function step taking an <automaton>, a current state name, and an input symbol. Given a state, step returns a list of the names of all possible states reachable from that state by travelling along exactly one edge from the current state (and that edge must have the appropriate label).
Hint: Remember the "last word of advice"!
Sample Output:
==> (step dfa1 'c 1)
(c)
==> (step dfa1 'd 0)
()
==> (step dfa1 'a 2)
()
==> (define nfa2
(create-automaton
'(a b c)
'((a a 0) (a b 0) (a b 1) (b a 1)
(b c 0) (c b 0) (c c 1))
'a
'(a)))
==> (step nfa2 'a 0)
(a b)
What to turn in:: Turn in your definition of step and output showing your function working.
Now, with step as our tool, we can simulate the operation of an automaton on an entire input sequence. We have given you a function, simulate, which takes in an automaton and an input "string" (technically, a list of characters--that is, things in the alphabet) and returns #t if the machine accepts the string and #f otherwise. The simulate function tracks all the states that the machine could be in after scanning each character of the input, and when it runs out of inputs, it checks to see whether any of the possible sequences puts it in a final state. If the machine could reach a final state by some choice of moves, then the machine accepts its input.
Important: We have given you simulate, however, it is important that you become just as familiar with the code as you would be if you had written it. We give you some sample output that you should read and understand.
Sample Output (uses DFA dfa1, defined previously):
==> (simulate dfa1 '(1 0 0 1))
#t
==> (simulate dfa1 '(1 0 1 1))
#f
==> (define (divis-by-3? n)
(simulate dfa1 (decimal->binary-list n)))
==> (divis-by-3? 12)
#t
==> (divis-by-3? 19)
#f
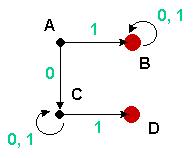The simulate function
works on NFAs (as you have seen, it works on DFAs as well, since they
are a subset of NFAs). An NFA is provided in the diagram. (The red
states are the final states and the start state is A. Transitions
labeled "0, 1" are just shorthand for two transitions which
have the same endpoints, but different labels. This NFA accepts
sequences which either begin or end with 1 (note that this is
or in the formal since, so a sequence that both begins and ends
with 1 will be accepted). This automaton is nondeterministic, since
from state C, given a 1, you can stay in C or go to D. The advantage of
this is that if you encounter a 1 in state C, you "choose" to
go to state D only if it's the last symbol in the sequence.
Well, this isn't a normal problem, and e isn't a normal number. And they both come between 2 and 3...
What to turn in: You should now test simulate with the NFA above. It is up to you to decide what constitutes sufficient sample output, and turn it in.
Warning: This may be the hardest question that you will be asked to solve all semester. Do not sit down and start hacking -- THINK!)
Write a function path? which, given a generic <graph> (we're leaving behind the world of automata) and two vertices, determines whether there is some path between the vertices. The function returns #t if some path exists and #f if there is no such path.
Think about this problem well before you start typing. You must write a paragraph description of your algorithm in addition to coding it!
Recommendations: Draw some graphs on a piece of paper, and think about how you would determine the answer for a given pair of vertices. Use ideas that you have developed over the previous problems. These aren't automata anymore, but you know more about graphs than you may expect. How is a general graph like an NFA?
In computer science, path? is generally known as a decision algorithm, since you are determining a property of the graph but not actually finding the path (but think about how you would do it, since it's going to be part of PS5).
Grading notes: This question will be graded as follows. Your code will be given a grade x out of n, for some positive integer n. Your paragraph will be given a grade y, out of 1. Your score for this question will be xy. This means write the paragraph! Also note that while efficiency isn't the focus of this problem, we may take off for needless inefficiency, so think about asymptotic running time as you work.
Sample Output:
==> (path? g1 (find-in-graph 'a g1) (find-in-graph 'e g1)) #t
What to turn in: Turn in your definition of path?, a paragraph description of how your algorithm works (you should write this before you start coding!), and demonstration that it works properly.
Now that you know the difference between an NFA and a DFA, we're going to introduce you to the subset construction, which allows us to convert any NFA to a DFA. Logically, the reasoning is thus. Imagine a pebble on the start state of our NFA (this can be done with multiple start states as well, but it's a bit trickier, which is why we're not addressing this scenario in the problem set). Given some input character or string, place pebbles on all possible states reachable by that input from any state that currently has a pebble on it (initially, this is just the start state) and call that set of states P. One of the states in your constructed DFA will be P, that is, each state of the DFA is a subset of all the states of the original NFA. From there, the next input character leads to the DFA state consisting of the subset of all NFA states reachable by that character from any of the states in the NFA subset, and so on.
One way of going about this would be to create all subsets of the states of the NFA and linking them up correctly to each other. As you may guess, this means the DFA of an NFA could potentially have exponentially more states (2n, specifically). Keep in mind, though, that some states are inaccesible from the start state. We have provide you a function that will help with this; it will be addressed later.
For example, take the NFA from Problem 2. The "raw" DFA would have states {A}, {B}, {C}, {D}, {AB}, {AC}, {AD}, {BC}, {BD}, {CD}, {ABC},{ACD}, {ABD}, {BCD}, and {ABCD}. For an example of an edge that would exist in the newly-created DFA, let us consider what occurs if we are currently in the DFA state {BC} (that is, in the NFA we can be on either B or C at this point in the input string). Taking input 1, B can go to B, and C could go to C or D, so the transition from {BC} on input 1 is {BCD}. The transition from {BC} on input 0 is {BC} again.
You will implement a function that translates any NFA (with one start state) to a DFA. The output of such a function, we have noted, is extraordinarily ugly. So we have provided a function remove-inaccessible-states which takes such an ugly DFA and attempts to clean it up in the manner which its name indicates. You probably should examine this function. But since, outside of debugging, there is no reason to look at the "raw" DFA, we have also provided a function nfa->dfa which applies remove-inaccessible-states to the result of passing the automaton to construct-subsets. So you need to write that function, which takes in an NFA, and returns a DFA which has states with names that are subsets of the states of the NFA (the creation of the names should be performed with the combine-names, provided in the source code), and the start state, edges, and accept states modified appropriately.
What to turn in: Turn in your definition of construct-subsets and output showing it working properly.
Last modified 7 October 1999, by jmv.