RESTRICTIONS: You are to work alone, and you may not use set!.
Before you do anything, please read about the entire homework carefully. It contains a wealth of good advice that can save you (and us) a lot of headaches later on. Turn in your code using the online submission system. Note that the due deadline is strictly enforced, and no late assignments will be accepted. A wise student would see this as an incentive to begin early!
If you have trouble with the course software or are generally stuck, remember that you have options. You may see a course staff member personally at our office hours or consulting hours. Alternatively, you can contact the course staff online and someone will respond to you within a reasonable amount of time.
Before getting started, we want to look at a few important concepts used in this problem set. As this is the first problem set, the goal is for you to become familiar with the Scheme language as well as understand recursion and generalization. The following describes some secondary concepts used by this problem set:
Side Effect - The fundamental idea behind functional programming is that every expression has a value. In general, whenever this rule is broken, it is due to a side effect. Side effects include assignments, input/output, and errors among other things. For much of this course, we will be analyzing the expressiveness and capabilities of programs that exclude side effects in total. However, for this problem set, we must use the display to draw the fractals; therefore, you must be able to distinguish a function that performs a side-effect from one that returns a value. Note that it is possible to have a function that performs a side-effect and returns a value, although this idea is not explored until later in the semester.
Turtle - For historical reasons, the graphics utility that draws the fractals is called a turtle. Essentially, the turtle is a point that faces in a particular direction. The turtle has three important functions (all which perform side effects). The first is turn which changes the direction that the turtle faces by rotating it counter-clockwise by a given number of degrees. Another function used by the turtle is draw which moves the turtle forward by a given number of pixels while drawing a solid line. Lastly, we also use the move function, which behaves in the same manner as draw except it does not draw a solid line.
In this problem set, you will be experimenting with fractals. Among the most famous fractals are the von Koch snowflake, first described by Helge von Koch in 1904, the Peano curve, the Hilbert curve, and the Cantor set. These figures not only look pretty, but also have important applications in many fields. For example, the Hilbert curve is used in dithering and compressing images.
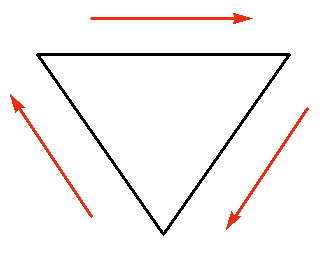
Many fractals can be specified by giving an initiator and a generator. The initiator is a starting shape, and the generator is a rule that can be applied to refine the shape. We can think of the initiator as a very rough initial approximation to the fractal. We can start with the initiator, then apply the generator as many times as we like to achieve better and better approximations. For the von Koch snowflake, the initiator is an equilateral triangle with sides oriented in a clockwise direction. (The red arrows show the direction of orientation only; they are not part of the figure.)
The generator of the von Koch snowflake is a rule that says: for any (oriented) line segment, remove the middle third and replace it by two sides of an equilateral triangle. The two new segments should extend to the left of the original segment when facing in the direction of orientation. That is, replace the oriented segment

by the four segments
oriented as shown.
To generate the fractal corresponding to a given initiator and generator, we conceptually generate a sequence of figures, each figure more refined than the last. The first figure is the initiator. The i + 1st figure is obtained by applying the generator to each oriented line segment in the ith figure. For the von Koch snowflake, the first figure would be the equilateral triangle, the second would be a six-pointed star, the third would be a six-pointed star with little bumps on each point, etc.
The fractal itself is the limit of these approximations. Fractals have a number of fascinating mathematical properties. They are self-similar, which means roughly that no matter how much you zoom in, the object still looks the same. They are continuous but nowhere differentiable. Their length is either 0 or infinite. One can define the dimension of a fractal in a natural way, and it turns out that their dimension is not 1 like curves or 2 like surfaces, but somewhere in between, which is why they are called fractals. The dimension of the von Koch snowflake is log 4/log 3 = 1.2618...
In this assignment you will construct level k approximations to fractals. These are the figures obtained by stopping the construction described above after stage k. For example, a level 1 von Koch snowflake consists of just an equilateral triangle; a level 2 von Koch snowflake is the six-pointed star; etc.
These figures can be created without having to actually generate the intermediate figures by using a recursive strategy for drawing a side of the figure. A level 0 side is just a straight line. A level k + 1 side is made up of several level k sides. In the von Koch snowflake, a level k + 1 side consists of four level k sides.
We can translate this strategy into a Scheme procedure that draws a side of a given level (specified by the parameter level) and of a given length (specified by the parameter length) using the current direction and from the current position, both specified in the turtle graphics package. If the level is 0, we simply draw a straight line of the given length. If the level is greater than 0, we recursively draw four sides of level level-1 and length length/3 in the appropriate directions relative to the initial angle.
(define (side length level)
(if (<= level 0)
(draw length)
(begin
(side (/ length 3) (- level 1))
(turn 60)
(side (/ length 3) (- level 1))
(turn -120)
(side (/ length 3) (- level 1))
(turn 60)
(side (/ length 3) (- level 1)))))
Note the use of begin. By reading the scheme quick reference, we see that it is used to group a sequence of side effects into one expression. This is necessary since the consequence of the if special form expects only a single expression.
Returning to our discussion of the side definition, the procedure draw draws a line segment by moving a graphic turtle using its current angle and the given distance. We can draw the level k snowflake by drawing three level k sides oriented at 120 degree intervals.
(define (snowflake length level) (turn 90) (move (- (/ length 2))) (turn -30) (side length (- level 1)) (turn -120) (side length (- level 1)) (turn -120) (side length (- level 1)) (turn -120) (turn 30) (move (/ length 2)) (turn -90))
See how these two definitions implement our strategy described above. snowflake is the initiator of the fractal, while side implements the generator. side performs the recursion necessary to approximate the fractal.
WARNING: Do not expect future problem sets to include detailed explanations of code as this one does. It will be increasingly important for you to know Scheme's features, which will be presented to you in lecture and is available in the scheme quick reference. Everything you need to complete any problem set is provided in the quick references.
Before beginning, you should take a moment to read what we have to say on the problem set submission page. Take time to read the style guide as well. A good portion of your grade will be on the style of your code. Also, take your time to look at an example solution to see a good way to format your code.
After opening DrSwindle (and updating to the latest version), check the definitions window and make sure it says "Advanced" next to "Language:". If it does not, choose "Configure Language" from the "Language" menu. Pick "Advanced" from the drop down menu. Click "Ok" and then click on the "Execute" button on top of the window. You should type (load ps1) in the definitions window. The load command should be the first thing in all problem set solutions you write. Following the load command, you should write your solutions to problems one through four, and the code for your nifty fractal if you choose to participate in the contest. Remember to separate the code for the different problems, as is done in the example.
For the moment, you can try out a few things. Start by evaluating the definitions window. This should bring up the turtle window. Due to a bug in DrScheme, the evaluator runs incredibly slow when the mouse pointer is over the turtle window, so try to move the pointer off the window. Now in the interactions window, type (snowflake 100 4) and press enter. This will draw a level 3 snowflake with a side-length of 100.
A useful function is clear which erases the window, but does not change the position nor direction of the turtle.
PRINCIPLE: Familiarity with Scheme
The snowflake figure is just one of a large family of figures that can be drawn using the same general function. Changing the generator and/or the initiator can completely change the shape of the figure.
Write a new generator function (flip-side length level) in which the first half of the oriented line segment is replaced with the two equal sides of an isosceles right triangle extending to the left and the last half with the two equal sides of an isosceles right triangle extending to the right.
It should be considered as 4 segments of equal length, not 3 segments.
Write a new initiator function square-snowflake that uses a square as the initial shape and flip-side as the generator. Try out your new initiator and see what kind of image it generates.
TURN IN: Please submit the new procedures square-snowflake and flip-side. The initiator function square-snowflake draws a square at level 0, just like the initiator function snowflake draws a triangle at level 0. The generator function flip-side draws the set of 4 line segments shown above, just like the generator function side draws the old set of four line segments.
PRINCIPLE: Functional abstraction, functions as parameters
In the initiator given to you and in the initiator you wrote, the shape of the generator is "hard-coded" i.e., right now, the initiator snowflake always uses the generator side. But it makes perfect sense to define line systems using any combination of generator and initiator. For instance, we should be able to use the square initiator with the original von Koch generator. What we need is some general way to glue together a generator and initiator so that we can try out different combinations.
One idea is to parameterize the initiator by the generator. That is, we could modify initiators so that they take the generator as an argument. Note that this involves passing a function as an argument.
Write two new functions, snowflake-1 and square-snowflake-1 based on snowflake and square-snowflake so that they take a generator function as an argument and invoke this generator instead of a hard coded one. Try out all four combinations of initiators and generators:
(snowflake-1 200 4 side)
(snowflake-1 200 4 flip-side)
(square-snowflake-1 200 4 side)
(square-snowflake-1 200 4 flip-side)
In particular, evaluating the first expression should yield the same figure as the original snowflake code. More precisely, for any integers ln and lv, (snowflake-1 ln lv side) yields the same drawing as (snowflake ln nv).
TURN IN: Please submit the two new procedures snowflake-1 and square-snowflake-1
PRINCIPLE: Functions as parameters
There is no reason why the generators should stay the same all the time, even in the same figure. Interesting designs can be obtained by inverting the generator on some levels.
We can easily invert an arbitrary generator by changing the signs of the angles that we add to the original heading. The decision whether to use a regular or inverted generator could be a function of the level; for example, we might decide to invert the generator on odd levels and not to invert on even levels. Alternatively, we might decide to invert on every third level, or we might decide to never invert at all.
To support an arbitrary inversion strategy, we need to pass a procedure inverter to the initiator which then passes inverter to the generator. The generator should call the inverter, passing in the current level, to determine the sign of the angle to add to the original heading. The inverter procedure should return either the u+ (unary plus) or u- (unary subtract) functions that will be used as a unary operator.
Implement the changes indicated above by adding the function inverter to the parameter list of snowflake and side, rewriting them as snowflake-2 and side-2 (don't forget to modify the functions called by these functions as well). To test your code, evaluate:
(snowflake-2 200 4 (lambda (level) u+))
and verify that you obtain the original snowflake figure as before.
You can also examine the result of evaluating:
(snowflake-2 100 4 (lambda (level) (if (odd? level) u+ u-)))
TURN IN: Please submit the new procedures snowflake-2 and side-2.
PRINCIPLE: Functional programming vs. side effects
Write two new procedures side-length and snowflake-length, that take the same type of arguments as the original procedures. However, instead of drawing anything, snowflake-length should return the total length of the figure that snowflake draws (i.e., the total distance moved by the pen), given the same arguments.
For example the expression (snowflake-length 100 0) should return 300, and (side-length 100 0) should return 100.
The overall structure of the two new procedures should be the same as the original, but each should return the length of the part of the figure that would have been drawn. It should be possible to do this with a minimal change to the original.
TURN IN: Please submit the procedures side-length and snowflake-length and a printout of the output generated by the following code (add it as a comment, see example):
(snowflake-length 100.0 4)
Hopefully, you generated some interesting snowflakes in the course of this assignment. If you wish, you can select your best designs and enter them in the CS212 Perfect Snowflake Contest. Submit the code which generates your snowflake and a printout of the result -- the code should be part of the file that you will send, but the printout should be given in the section on Monday evening (9/6) or the lecture on Tuesday morning (9/7). To be fair, please do not turn in more than two pictures. Designs will be judged by the CS212 staff. The winner will receive a prize.
Notes: