Next: Higher-Order Functions (10 points) Up: CS212 Preliminary Exam I Previous: Evaluation of Dylan Expressions

Analysis of Algorithms (30 points)

You are to analyze the running time for a function tail-sums (defined below). The function takes a list of numbers, say n₁, n₂, ... , n_m and returns a list of numbers s₁, s₂, ... , s_m where .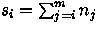

     (define (sum-list <function>)
         (method ((x <list>))
            (if (null? x) 0 (+ (head x) (sum-list (tail x))))))

     (define (tail-sums <function>)
         (method ((y <list>))
            (if (null? x) '() (pair (+ (head x) (sum-list (tail x)))
                                      (tail-sums (tail x))))))

For example: (tail-sums '(1 2 3 4 5)) evaluates to the list '(15 14 12 9 5).

a.

tail-sums is defined in terms of sum-list. What is the running time (using big-O notation) of sum-list in terms of n, the length of the input list x? (You need not justify your answer.)

 

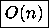
b.

Write out a set of recurrence equations that summarizes the time to run tail-sums in terms of the length m of the input list y. Be sure to give equations for T(0) (the time to run tail-sums on an empty list) and for T(m+1). The latter should be expressed in terms of T(m) and the time to run sum-list on a list of length m.

1.

T(0) = c₀

2.

T(m+1) = c₁ + m + T(m)

 

c.

Determine a closed form solution (i.e., a single definition for T(m) without any recurrence) for the running time of tail-sums. Use big-O notation to express the result.

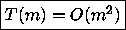
d.

Write a new function, tail-sums-2, which is asymptotically more efficient than tail-sums.

(define (tail-sums-2 <function>)
  (method ((x <list>))
    (cond ((null? x) '())
          ((null? (tail x)) x)
          (else: (bind (((t <list>) (tail-sums-2 (tail x)))
                        ((i <integer>) (+ (head x) (head t))))
                    (pair i t))))))

Next: Higher-Order Functions (10 points) Up: CS212 Preliminary Exam I Previous: Evaluation of Dylan Expressions