Representing Java Values

The Java language abstraction vs. hardware implementation

The Java language is an abstraction. Java is implemented on top of hardware using a compiler and the software for its run-time system, presenting you with the illusion that there are really ints, booleans, objects, and so forth. In reality there are circuits and electrons. For most part, you can ignore the lower-level details of what is really happening when Java programs run. That's because the Java abstraction is very effective. But computer scientists ought to have a model of how computers really work.

Memory, memory addresses, and words

The computer memory is actually a big grid in which a bit is stored at every intersection. But the hardware itself offers a more abstract view of memory as a big array. The memory can be accessed using memory addresses that start at 0 and go up to some large number (usually 2³² or 2⁶⁴, depending on whether the computer is 32-bit or 64-bit). Each address names a group of 8 bits (a byte). However, usually computer memories give back multiple bytes at once. When given an address divisible by four, the computer memory can read the four bytes beginning at that address, containing 32 bits. These four bytes are called a word. On 64-bit machines, the memory can fetch 64 bits at a time; for simplicity we'll call a set of eight bytes a double word.

Integral types (`int`, `short`, `byte`) and signed (two's-complement) representations.

Internally, computers represent numbers using binary (base 2) numbers rather than the decimal (base 10) representations we've grown up with. In base 2, there are only two possible digits, 0 and 1, which can be represented in the computer's hardware as a switch that is turned off or on, or a voltage that is low or high.

Binary digits stand for coefficients on powers of two rather than on powers of ten, so 1101₂ = 8₁₀ + 4₁₀ + 0 + 1 = 13₁₀. (Note that we write a subscript 2 or 10 to indicate the base of a number when there is ambiguity.)

In base 10, a number of n digits can represent any number from 0 up to but not including the number 10ⁿ. For example, in three decimal digits we can represent any number between 0 and 999 = 10³-1. Similarly, n binary digits can represent any number from 0 up to 2ⁿ-1. Therefore, a byte containing 8 bits could represent any number between 0 and 255, since 2⁸ = 256. The Java char type is a 16-bit number, so it can have any value between 0 and 2¹⁶-1 = 65535. A 32-bit word can represent any number between 0 and 2³²-1 = 4294967295.

That may sound good enough for most uses, but what about negative numbers? To handle them, we need a way to represent the sign of a number.

Signed: int (32 bits), short (16 bits), long (64 bits), byte (8 bits)
Unsigned: char (16 bits, 0–65535)

Two's complement representation: in a signed n-bit representation, the most significant bit stands for -2^n-1 instead of 2ⁿ⁻¹, which would be its value in the unsigned representation we have been discussing above. For Java's type byte, the bits 01111111 represent 127 but 10000000 is −128.

Adding these together as binary numbers in the usual way, we get 11111111, which represents −1, just as we'd expect when we add −128 and 127. Adding one more to this—and dropping the final carry—we have 00000000, the representation of 0, also as we would like. Some other representations for bytes are as follows:

−7	11111001
−4	11111100
−2	11111110
−1	11111111
0	00000000
1	00000001
2	00000010
4	00000100
7	00000111

In effect, going from an unsigned representation to a two's-complement signed representation takes the upper half of the representable numbers and makes them wrap around to become negative numbers. This works because numeric computations are done modulo 2ⁿ, and 128 and −128 are the same number modulo 2⁸.

Everything we have said about the byte applies to the other signed Java types (short, int, and long), except that those types have more bits (16, 32, and 64 respectively).

An interesting identity is that to negate a number, you simply invert all of its bits and then add one, discarding any final carry. Considering bytes, we have −1 = 11111110 + 1 = 11111111. What about negating 0? In this case, −0 = 11111111 + 1 = 100000000, but this is just 0 once we discard the 9th digit.

Other representations for numbers exist, such as one's-complement, in which the negation of a number is performed by inverting all of its bits. But the usual two's-component representation is more convenient to work with and leads to simpler, faster implementations in hardware. At this point essentially everyone uses two's complement.

Arrays, objects, and pointers

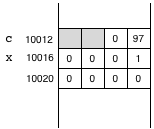
When Java variables are stored in the computer's memory, they may take up more space than the number of bits indicated. In particular, variables are stored in memory on word boundaries and always take up an integral number of words. So variables with types short, int, byte, and char all take up one full word, whereas variables with type long take up two consecutive words. For example, given the variable declarations

char c = 'a';
long x = 1;

we might find variables c and x stored in consecutive memory locations 10012–10023 as in the following figure showing the contents of each byte. Notice that the high 32 bits of x are all zero, and that the high 16 bits of the word containing c are unused.

Fields of objects (instance variables) are stored in the same way as variables, taking up an integral number of words that are located contiguously in memory.

For example, consider the following code:

class A {
    char c;
    B y;
}
class B {
    long z;
}
...
B b = new B();
b.z = 1;
A a = new A();
a.c = 'a';
a.y = b;

Suppose that object b is located at memory location 14404 and object a is located at 22288. Then memory looks something like the following:

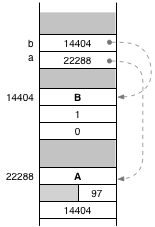
Notice that each object starts with one header word that describes its class. This word actually contains a pointer to another memory location that is shared by all objects of that class.

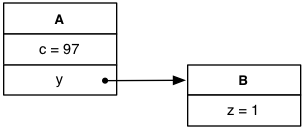
Because the actual memory addresses don't matter, it is sufficient for understanding this program to look at the simpler object diagrams we have been using:

Floating point representations

Java supports floating-point numbers that act a lot like real numbers. But it takes an unbounded amount of memory to store a real number, so floating-point numbers are only an approximation. There are two floating-point types in Java. The type float is a single-precision floating point number taking up one word, and the type double is a double-precision floating point number taking up two words.

It is possible to see how floating point numbers are represented in Java by using the methods Float.floatToRawIntBits and Double.doubleToRawLongBits(double), which return an int and a long containing the same bits as the respective float and double. Attached to these notes is some code that uses these methods to explore how floating point numbers are represented.

According to the IEEE 754 specification, which is almost universally followed at this point, A single-precision floating point number is represented as shown:

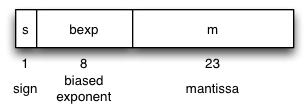
A floating point number is represented using three components, the sign, the exponent, and the mantissa, respectively taking up 1, 8, and 23 bits of the 32-bit word.

Given components s (sign), exp (exponent), and m (mantissa), where the exponent is between −126 and 127, the floating point number represents the real number

(−1)^s·2^exp·(1.m)

Here, we intepret m as a sequence of binary digits, so “1.m” represents a binary number that is at least 1 (and equal to 1 in the case where m = "000000...") and less than 2. The maximum number that 1.m can represent is "1.11111...", which is a binary representation of a number less than 2 by the small amount 2⁻²³.

Thus, if we want to represent the number 1, we choose s=0, exp=0, m=0000... . To represent numbers outside the interval [1,2), an exponent is needed. To represent 2, we use s = 0, exp = 1, m=0000..., since 1·2¹ = 2. To represent 3, we choose s=0, exp=1, m=10000..., since 1.1 in binary represents 3/2, and 3/2·2¹ = 3. And so on.

The exponent is stored with a “bias” or offset of 127, so the actual bit-level representation of 1.0 has s = 0, bexp = 01111111, m = 00000000000000000000000, and the whole word contains exactly the bits 00111111100000000000000000000000.

Some special exponents follow different rules. If the exponent is −127 (and hence the biased exponent is 0), the represented number is instead:

(−1)^s·2⁻¹²⁶·(0.m)

Therefore, a word consisting entirely of 0's represents the floating point number 0.0, since 0.m = 0 in that case. It is also possible to represent the floating point number −0.0, which behaves slightly differently, such as when its reciprocal is computed.

An exponent of 128 is represented by a biased exponent of 255 (all 1's). “Numbers” represented with this exponent include positive and negative infinity, with a mantissa of 0 and the appropriate sign bit. If the mantissa is anything other than 0, the represented “number” is called NaN, for “not a number”. The value NaN arises when there is no reasonable answer to the computation, such as when adding positive and negative infinity. Any computation performed using NaN produces NaN, so a final result of NaN indicates that something went wrong during the computation.

A single decimal digit corresponds to log₂ 10 = 3.32 bits, so the number of decimal digits represented by 23 bits of mantissa is 23/3.32 = 6.93. You can therefore think of floating point numbers as representing numbers to about 7 digits of precision. However, errors tend to accumulate with each computation, so a long computation often has fewer digits of precision. For example, if you subtract 1000000.0 from 1000000.1, the result will be 0.1 but with only 1 digit of precision. In fact, as the attached code showed, the result is reported to be 0.125. Oops!

The other thing to watch out for is that the order of operations may affect what you compute, because rounding gets done at different places. Just because two formulas produce the same real number doesn't mean they will produce the same floating-point number. As a result, it is usually necessary when comparing two floating-point numbers for equality to instead check that their difference lies within some tolerance corresponding to the largest expected round-off error.

The largest number representable using float is Float.MAX_VALUE, which is about 3.0·10³⁸. And the smallest positive number representable with full precision is about 10⁻³⁸. It is possible to represent smaller numbers down to about 10⁻⁴⁵ using the denormalized representation in which the exponent is −127, but in this case the precision of the number is reduced.