CS 2112 Recitation 6 : Top-down parsing

How to approach assignment 4

You will be more successful on the next assignment if you divide the work up evenly between the two partners and set things up so both can make progress immediately. In particular, you don't want to wait on implementing the fault injection/mutation part of the assignment, because it's about half the work all by itself. The natural interface between parsing and fault injection is the design of the AST. If your group can arrive at a good AST design early, then one partner can work on producing the AST as an output and the other can work on fault injection that uses it as an input.

Interpreting an expression as AST

We looked at an example rule written in the critter language and drew the corresponding AST. Here is a rule:

mem[8] mod (6 + 7 + 11) = 0 and 1 < mem[2] --> mem[2] := 5 mem[1+mem[3]] := 2 + ahead[4] left

Here is a reasonable way to represent it as an abstract syntax tree:

It might be useful see the DOT source file that generated this diagram. It can be viewed using Graphviz.

Notice that we created nodes called "command" and "updates" that aren't in the concrete syntax.

Parsing example: s-expressions

The second high-level programming language, Lisp, is written using s-expressions, introduced by John McCarthy around 1959. An s-expression uses parentheses to denote the application of a function, in prefix syntax. For example, the expression 2+3 would be written as (+ 2 3) in Lisp. The tokens "+", "2", and "3" are all considered identifiers.

A grammar for s-expressions

S → id | ( L )
L → S L | ε

L → S L | S

AST for s-expressions

The abstract syntax tree need not follow the parse tree closely. In the case of s-expression, there are really two kinds of expressions: identifiers and applications. We can capture this idea by declaring two classes that implement a common Node interface:

interface Node {
    ...
}
class Id implements Node {
    String name;
}
class App implements Node {
    List<Node> children;
}

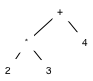
So an s-expression such as (+ (* 2 3) 4 ) produces the following AST, where all non-leaf nodes represent function applications.

Parsing s-expressions

We declare a method for each nonterminal, with a type appropriate for representing what that nonterminal corresponds to. One trick we can use is to rewrite the L nonterminal using EBNF syntax in which a regular expression is used on the right-hand side:

L → S*

This rule suggests implementing the parsing of L as a loop.

Node parseS() {
    if (peek().isIdentifier()) {
	return new Id(nextToken());
    } else if (peek().equals("("))) {
	consumeToken("(");
	List<Node> children = parseL();
	consumeToken(")");
	return new App(children);
    }
}

List<Node> parseL() {
    List<Node> nodes = new LinkedList<Node>;
    while (!peek().equals(")"))
	nodes.append(parseS());
    return nodes;
}

This parsing code is simple and efficient.