Lecture 20: Loop invariants and searching
A loop invariant is a condition that is true at the beginning and end of every loop iteration. When you write a loop that works correctly, you are at least implicitly relying on a loop invariant. Knowing what a loop invariant is and thinking explicitly about loop invariants will help you write correct, efficient code and to develop tricky algorithms.
Binary search via tail recursion
/** Returns an index i such that a[i] == k.
Requires: k is in a[l..r], elements in a are in ascending sorted
order, l <= r.
Performance: O(lg(n)) where n = r-l+1
*/
int search(int[] a, int l, int r, int k) {
if (l==r) return l;
int m = (l + r)/2;
if (k <= a[m])
return search(a, l, m, k);
else
return search(a, m+1, r, k);
}
Note that we use the notation i..j to denote the set {x | i ≤ x ≤
j} = {i,i+1,...,j-1,j}. We use the notation a[i..j] to indicate
the subsequence of the array a starting from a[i] and continuing
up to and including a[j].
This algorithm is deceptively tricky to get right. It's pretty easy to
get close, but how do we know we got the computation of m right?
Why is it k <= a[m] and not k < a[m]? Why m and m+1 in the two
recursive calls to search? If we change any of these decisions, the
algorithm may fail to find the correct element and may even fail to terminate.
Binary search via iteration
Since the recursive algorithm is tail-recursive, we can convert it into code that uses a loop. It will run a bit faster in Java because in Java, loops are faster than recursion.
int search(int[] a, int l, int r, int k) {
while (l < r) {
int m = (l+r)/2;
if (k <= a[m]) r = m;
else l = m+1;
}
return l;
}
The precondition of the recursive implementation becomes a loop invariant with three clauses:
- k ∈
a[l..r] -
ais sorted in ascending order -
l≤r
In general, we can think of a loop invariant as the precondition of a tail-recursive implementation of the loop.
If we know what the loop invariant is for a loop, it is often a good
idea to document it. In fact, we can document it in a checkable way
by using an assert statement that is executed on every
loop iteration. This is just like writing an assert to
check the precondition of the tail-recursive version of the same code.
Using loop invariants to show code is correct
Loop invariants can help us convince ourselves that our code, especially tricky code is correct. They also help us develop code to be correct in the first place, and they help us write efficient code.
To use a loop invariant to argue that code does what we want, we use the following steps:
- Initialization.
Show that the loop invariant is true at the very beginning of the loop.
- Maintenance.
Show that if we assume the loop invariant is true at the beginning of the loop, it is also true at the end of the loop. (Other than coming up with the loop invariant in the first place, this is usually the trickiest step.)
- Postcondition.
Show that if the loop guard is false (so the loop exits) and the loop invariant still holds, the loop must have achieved what is desired.
These three steps allow us to conclude that the loop satisfies partial correctness, which means that if the loop terminates, it will succeed. To show total correctness, meaning that the loop will terminate, there is a fourth step:
- Termination. Show that some quantity decreases on every loop iteration, and that (assuming the loop invariant holds), it cannot decrease indefinitely without making the loop guard false.
Let's try these four steps on the binary search algorithm.
Initialization. The loop invariant holds initially because it is the precondition of
search().Maintenance. To keep track of how the variables change during the loop, let's use the names l' and r' to refer to the values of l and r at the end of the loop body. Our goal is to show that if the loop invariant holds at the beginning on l and r, then it holds at the end on l' and r'.
First, we need to show that l'≤r'. In the first arm, r' = m = (l+r)/2, which is clearly at least as large as l=l', since the loop guard ensures l<r. In the second arm, l' = m = (l+r)/2 + 1. Again, since the loop guard ensures l≤r-1, we have (l+r)/2+1 ≤ (2r - 1)/2 + 1 = r.
We've just shown that l ≤ m ≤ r. We know that either k ∈ a[l..m] or k ∈ a[m+1..r]. Now, consider each of the two arms of the
ifstatement. If k ≤ a[m], we know that k ∈ a[l..m]; if it were in a[m+1..r] then by the invariant, k would have to be greater than a[m]. If k > a[m], on the other hand, we know that k ∈ a[m+1..r]. In either arm, we know that k ∈ a[l'..r'].-
Postcondition. If the loop guard is false but the loop invariant holds, then clearly l=r. In this case, the loop invariant guarantees that a[l] = k. So l (or r) is the correct result to return.
-
Termination. The quantity
r-lmust be nonnegative by the loop invariant and it can never become smaller than zero, at which point the loop terminates. We also need to show that this quantity becomes strictly smaller on each iteration. This is ensured because if l<r, l ≤ m = (l+r)/2 < r. The number of elements is nonzero in both a[l..m] and a[m+1..r].
Example: Exponentiation by squaring and multiplication
Here is an implementation of exponentiation that is efficient but whose correctness is not instantly apparent.
/** Returns: x^e.
* Requires: e >= 0.
* Performance: O(lg(e))
*/
int pow(int x, int e) {
int r = 1;
int b = x;
int y = e;
// loop invariant: r·b^y = x^e
while (y > 0) {
if (y % 2 == 1) r = r * b;
y = y/2;
b = b*b;
}
return r;
}
Let's consider the four steps outlined above.
- Initially, r=1, b=x and y=e, so trivially we have r·b^y = x^e.
- Let us use y', b', and r' to refer to the values of these variables
at the end of the loop. We need to show that if r·b^y = x^e at the beginning,
then r'·b'^y' = x^e at the end. There are two cases to consider:
- y is even. In this case, r' = r, y' = y/2, and b'= b2. Therefore, r'·b'^y' = r·(b2)y/2 = r·b^y, as desired.
- y is odd. Here we have r'=r·b, y' = (y-1)/2, and b' = b2. Therefore, r'·b'^y' = r·b·(b2)(y-1)/2 = r·b·(b)(y-1) = r·b^y, again.
- If the loop guard is false, then y = 0, because y can never become negative by dividing it by 2. If y = 0, then r·b^y = r, so r must be equal to x^e.
- Dividing by two makes the quantity y smaller on every loop iteration, because it is always nonnegative (nonnegativity is actually a second clause in the loop invariant). It can never become negative, so eventually it will become zero and the loop will terminate.
Therefore, the loop terminates and computes the correct value for x^e in variable r.
Example: Insertion sort
/* Effect: put array a into ascending sorted order
*/
void sort(int[] a) {
// invariant: a[0..i-1] is in sorted order
for (int i=1; i < a.length; i++) {
int k = a[i];
// invariant: the element a[0..i], excluding a[j], are in sorted order
// and contain all the elements found originally in a[0..i-1].
for (int j = i; j > 0 && a[j-1] > k; j--) {
a[j] = a[j-1];
}
a[j] = k;
}
}
There are two loops, hence two loop invariants. These loop invariants can be visualized with the following diagram:
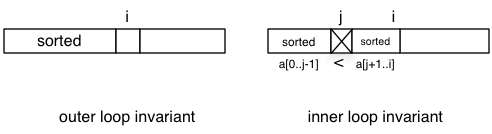
Notice that the loop invariant holds in for loops at the point
when the loop guard (e.g., i < a.length) is evaluated, and
not necessarily at the point when the for statement starts
executing.