We're now going to start talking about data structures and algorithms. A data structure is simply a graph of objects linked together by references (pointers), often in order to store or look up information.
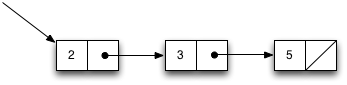
Perhaps the most classic example of a data structure is the linked list. A linked list consists of a set of node objects in which each node points to the next node in the list. Some data is stored along with each node. This data structure can be depicted graphically as shown in this figure, where the first three prime numbers are stored in the list.

The last node in the list does not point to another node; instead, it refers to
the special value null or, alternatively, to a sentinel
object that is used to mark the end of the list.
A linked list node is implemented with code like the following:
class Node {
Object data;
Node next; // may be null
}
The information in the list may be contained inside the nodes of the linked list, in which case the list is said to be endogenous; it may also be merely linked from the list node, in which case the list is exogenous.
A sentinel value can be substituted for the value null, avoiding the
problem of null pointer exceptions:
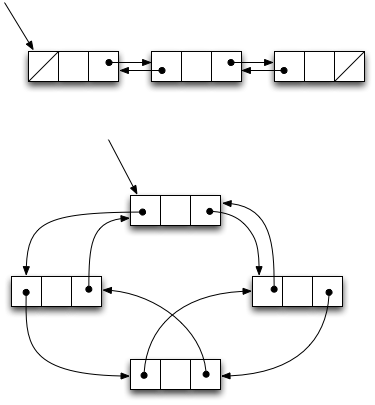
static Node Null = new Node();The list shown above is considered a singly linked list because each list node has one outgoing link. It is sometimes helpful to use a doubly linked list instead, in which each node points to both the previous and next nodes in the list. In a doubly linked list, it is possible to walk in both directions.
The definition of a doubly linked list node looks something like the following:
class DNode {
Node prev, next;
Object data;
}
Doubly linked lists come in both linear and circular varieties, as
illustrated below. In the linear variety, the first and last nodes have
null prev and next pointers, respectively. In the
circular variety, no pointers are null. There is a
head node distinguished by the fact that a pointer is kept to it from outside.
The class java.util.LinkedList is actually implemented as a
circular doubly linked list.
We can use lists to build many interesting algorithms. Usually we keep some small number of variables
pointing into the list, and follow the pointers between nodes to get around. For example, we can write
code to check whether a list contains an object equal to a particular object x:
boolean contains(Node n, Object x) {
while (n != null) {
if (x.equals(n.data)) return true;
n = n.next;
}
return false;
}
We can also scan over a list accumulating information. For example, we might compute the total of all the numbers contained in a list of integers:
int total(Node n) {
int sum = 0;
while (n != null) {
sum += n.data;
n = n.next;
}
return sum;
}
Linked lists are useful data structures, but using them directly can lead to programming errors. Often their utility comes from using them to implement other abstractions.
For example, we can use a linked list to efficiently implement an immutable list of objects:
// An immutable, ordered, finite sequence of objects (a0,
// a1, ..., an-1), which may be empty.
interface ImmList {
/** Returns: the first object in the list (a0).
* Checks: the list is not empty. */
Object first();
/** Returns: a list containing all elements but the first, i.e.,
* (a1, ..., an-1)
* Checks: the list is not empty. */
ImmList rest();
/** Returns whether this is the empty list. */
boolean empty();
/** Returns: a list containing the same elements as this,
* but with the object x inserted at the beginning. That is,
* (x, a1, ..., an-1)
* Checks: the list is not empty. */
ImmList cons(Object x)
}
To implement this interface using a null-terminated list, we will
need an additional header object so that we can represent empty lists
with something other than null. (Notice that we don't bother to
repeat the specifications from the interface. No need!)
class ImmListImpl implements ImmList {
private Node head; // may be null to represent empty list
public ImmListImpl() {
head = null;
}
public boolean empty() {
return (head == null);
}
public Object first() {
assert head != null;
return head.data;
}
public ImmList rest() {
assert head != null;
ImmListImpl r = new ImmListImpl();
r.head = head.next;
return r;
}
public ImmList cons(Object x) {
ImmListImpl r = new ImmListImpl();
r.head = new Node(x, head); // assuming appropriate Node constructor
return r;
}
}
Notice that this implementation allows different lists to share the same list
nodes. This makes operations like cons and rest much
more efficient than they otherwise would be. It is safe to share list nodes
precisely because the list abstraction is immutable, and the underlying list
nodes cannot be accessed by any code outside the ImmListImpl
class. Abstraction lets us build more efficient code.
ImmList is immutable, it makes sense to have an equals
operation that compares all the corresponding elements:
boolean equals(Object o) {
if (!o instanceof ImmList) return false;
ImmList lst = (ImmList) o;
Node n = head;
while (n != null) {
if (lst.empty()) return false;
if (!n.data.equals(lst.data)) return false;
n = n.next;
lst = lst.rest();
}
return lst.empty();
}
The sharing that was possible with immutable lists is necessarily lost when we use linked lists to implement mutable lists. On the other hand, we can offer a larger set of operations:
/** A mutable ordered list (a0, a1, ..., an-1) */
interface MutList {
/** The number of objects in the list. */
int size();
/** Returns: The object at index i (ai).
* Requires: 0 ≤ i < n */
Object get(int i);
/** Effects: Inserts x at the head of the list. */
void prepend(Object x);
/** Effects: Inserts x at the end of the list. */
void append(Object x);
/** Returns: true if x is in the list.
* Effects: Removes the first occurrence of object x from the list. */
boolean remove(Object x);
/** Returns: true if x is in the list. */
boolean contains(Object x);
...more operations...
}
Again, this abstraction can be implemented using a linked list. A header object is again handy, especially to keep track of auxiliary information like the number of elements in the list.
class MList implements MutList {
private Node head;
private int size_; // invariant: size_ is the number of nodes in the list starting with head.
// private Node last; // needed if "append" is to be efficient.
int size() { return size_; }
void prepend(Object x) {
head = new Node(x, head);
size_ ++; // restore the size_ invariant
}
boolean remove(Object x) {
Node n = head, p = null;
while (n != null && !x.equals(n.data)) {
p = n;
n = n.next;
}
if (n == null) return false;
size--;
if (p == null) head = n.next;
else p.next = n.next;
return true;
}
}
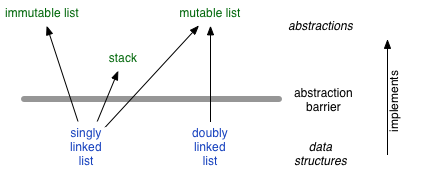
A key thing to observe here is that data structures such as singly or doubly linked lists are data structures. We can use these data structures to implement abstractions, such as immutable lists and mutable lists, which provide a particular set of operations. There are other ways to implement these abstractions, however, as we'll see later. And we can use these data structures, in turn, to implement other abstractions. For example, one useful abstraction we will see over and over again is the stack. A stack is an ordered list that supports two operations:
void push(Object x) : insert the element x at the beginning of the list.
Object pop() : remove and return the first element in the list. Requires that the stack is non-empty.
The stack abstraction is easily and efficiently implemented using linked lists:
class Stack {
private Node top;
void push(Object x) {
top = new Node(x, top);
}
Object pop() {
Object ret = top.data;
top = top.next;
}
The key is to keep in mind that data structures are implementations of abstractions.