Please let me know via email (chew@cs.cornell.edu) if you find mistakes in the solutions. Past experience indicates that I may have made some.
a) Write a Java class method named append that takes two non-empty
linked lists L1 and L2 as parameters, and updates the last cell of L1 so that it
points to the first cell of L2. The method does not return
anything. The lists are built using the ListCell class given below.
public static void append (ListCell L1, ListCell L2) {
ListCell finger = L1;
while (finger.getNext() != null)
finger = finger.getNext();
finger.setNext(L2);
}
b) What is the asymptotic complexity of your algorithm, expressed as a
function of n1 and n2, where n1 is the number
of elements in L1 and n2 is the number of elements in L2,
respectively? Justify your answer (briefly).
This is an O(n1) algorithm because the
number of iterations of the while-loop is equal to n1. Each
iteration performs a constant amount of work.
class ListCell {
protected Object datum;
protected ListCell next;
public ListCell (Object x, ListCell n) {
datum = x;
next = n;
}
public Object getDatum () {
return datum;
}
public ListCell getNext () {
return next;
}
public void setDatum (Object x) {
datum = x;
}
public void setNext (ListCell l) {
next = l;
}
public String toString () {
if (next == null) return datum.toString();
else return datum.toString + " " + next.toString();
}
}
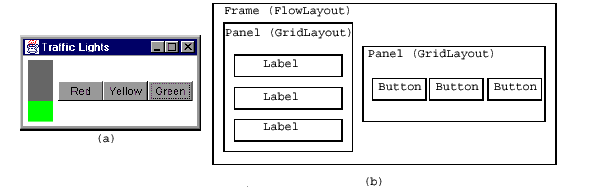
The GUI is shown in Figure (a) and the containment hierarchy is shown in Figure (b). Note that the picture is taken from an old exam (before javax.swing was released); thus, you should substitute JLabel for Label, JButton, for Button, JPanel for Panel, and JFrame for Frame. The skeleton code is provided below. Write the method createGUI() which creates the GUI according to the containment hierarchy in Figure (b), and the method addListeners() which creates and adds the relevant listeners to the relevant sources. The user should be able to terminate the program when the “close-box” of the top-level window is clicked.
import java.io.*;
import java.awt.*;
import java.awt.event.*;
import javax.swing.*;
/**
* Pseudo Traffic Lights
*/
public class PseudoTrafficLights extends JFrame {
private JPanel lightsPanel;
private JLabel redLightLabel;
private JLabel yellowLightLabel;
private JLabel greenLightLabel;
private JPanel buttonsPanel;
private JButton redLightBtn;
private JButton yellowLightBtn;
private JButton greenLightBtn;
// Constructor
public PseudoTrafficLights() {
super("Traffic Lights");
// Create the GUI
createGUI();
// Add the listeners to the sources
addListeners();
// Pack and show the window
pack(); // Makes window fit tight around its contents
setVisible(true);
}
// The main method
public static void main (String[] args) {
new PseudoTrafficLights();
}
// Helper method to terminate the program
private void terminate() {
dispose();
System.exit(0);
}
// a. (13 points) Write method createGUI to set up the GUI.
private void createGUI() {
redLightLabel = new JLabel(" "); // changed
yellowLightLabel = new JLabel(" ");
greenLightLabel = new JLabel(" ");
redLightLabel.setBackground(Color.gray);
yellowLightLabel.setBackground(Color.gray);
greenLightLabel.setBackground(Color.green);
redLightLabel.setOpaque(true); // added
yellowLightLabel.setOpaque(true); // added
greenLightLabel.setOpaque(true); // added
lightsPanel = new JPanel(new GridLayout(3,1));
lightsPanel.add(redLightLabel);
lightsPanel.add(yellowLightLabel);
lightsPanel.add(greenLightLabel);
redLightBtn = new JButton("Red");
yellowLightBtn = new JButton("Yellow");
greenLightBtn = new JButton("Green");
buttonsPanel = new JPanel(new GridLayout(1,3));
buttonsPanel.add(redLightBtn);
buttonsPanel.add(yellowLightBtn);
buttonsPanel.add(greenLightBtn);
getContentPane().setLayout(new FlowLayout());
getContentPane().add(lightsPanel);
getContentPane().add(buttonsPanel);
}
// b. (12 points) Write method addListeners to add listeners to the sources
private void addListeners() {
greenLightBtn.addActionListener( new ActionListener() {
public void actionPerformed(ActionEvent evt) {
greenLightLabel.setBackground(Color.green);
yellowLightLabel.setBackground(Color.gray);
redLightLabel.setBackground(Color.gray);
}
});
yellowLightBtn.addActionListener( new ActionListener() {
public void actionPerformed(ActionEvent evt) {
greenLightLabel.setBackground(Color.gray);
yellowLightLabel.setBackground(Color.yellow);
redLightLabel.setBackground(Color.gray);
}
});
redLightBtn.addActionListener( new ActionListener() {
public void actionPerformed(ActionEvent evt) {
greenLightLabel.setBackground(Color.gray);
yellowLightLabel.setBackground(Color.gray);
redLightLabel.setBackground(Color.red);
}
});
addWindowListener( new WindowAdapter() {
public void windowClosing(WindowEvent evt) {
terminate();
}
});
}
}
(a) Java Nagila, a CS211 student, implemented a bunch of algorithms and came up with the following running times as a function of input size. Using big-O notation, write down the simples and most accurate expressions for the complexity of these algorithms.
(b) You have an algorithm that runs in time O(log n). Java Nagila
claims to have found a better algorithm that runs in time O(log(n-1)). Is
either algorithm better than the other in an asymptotic sense? Explain
your answer briefly using the formal definition of big-O notation.
No, in the asymptotic sense they are both the
same. To see this, note that log(n-1) < log(n) for all n>2;
thus, by definition, log(n-1) = O(log n) for c=1 and N=2. Note also that n
< (n-1)2 for n>3. Taking the log of each side, we
get log n < 2 log(n-1) for n>3. Thus, by definition, log n =
O(log(n-1)) for c = 2 and N = 3.
(c) The following method returns the ith element of an integer list.
public static int element (List list, int i) {
if (i == 1) return list.first();
else return element(list.rest(), i-1);
}
What is the asymptotic time complexity of accessing the mth
element of a list using this method? Express the complexity as a function
of m and n, the length of the list.
To get to the mth element, we make m calls to element()
where each call takes constant time. Thus the total time is O(m).
[This method could be improved by checking for i < 0.]
| Data Structure | insert | find | getMin | successor |
|---|---|---|---|---|
| sorted array | O(n) | O(log n) | O(1)* | O(log n) |
| unsorted array | O(1) | O(n) | O(n) | O(n) |
| balanced tree | O(log n) | O(log n) | O(log n) | O(log n) |
| hashtable | O(1)** | O(1)** | O(n) | O(n) |
| sorted linked list | O(n) | O(n) | O(1)* | O(n) |
| unsorted linked list | O(1) | O(n) | O(n) | O(n) |
*For both the sorted array and sorted list we can't tell if the array is in descending or in ascending order. In such a situation, it's reasonable to assume that the order used is the one that provides the best time bounds. Thus, for getMin() in the sorted array we assume the array is in descending order so that we don't have to move any of the data after we get the min value. For getMin() in the sorted linked list, we assume the array is in ascending order so that we can can quickly locate the minimum.
**For the Hash Table, I am assuming that table doubling is being used.
The following picture represents a BST (Binary Search Tree).
(22)
/ \
(14) (25)
/ \ / \
(11) (16) (23) (40)
\ /
(24) (32)
(22)
/ \
(14) (25)
/ \ / \
(11) (16) (23) (40)
/ \ /
(15) (24) (32)
(22)
/ \
(14) (32) Used the successor.
/ \ / \
(11) (16) (23) (40)
\
(24)| word | ape | bat | bird | carp | dog | hare | ibex | mud | koala | stork |
|---|---|---|---|---|---|---|---|---|---|---|
| h | 6 | 0 | 6 | 7 | 0 | 2 | 0 | 6 | 1 | 8 |
Draw a picture of the resulting hashtable (using chaining) after inserting, in order, the following words: ibex, hare, ape, bat, koala, mud, dog, carp, stork. Which cells are looked at when trying to find bird? What is the load factor (lambda) for the hash table?
| chaining | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
If you try to find "bird" then you'll search cells ape and mud. The load factor is n/m = 9/11.
| BST (Dictionary) | Max-Heap (Priority Queue) |
|---|---|
5
/ \
3 6
/ \
1 4
\
2
|
6 / \ 3 4 / \ 1 2 |
For each of the preceding trees, find a sequence of appropriate
operations that will produce it starting from an empty tree.
There are lots of sequences that will do this.
Here's one possible sequence for the BST: Insert 5, 3, 6, 1, 4, 2. Here's
one for the Max-Heap: Insert 6, 3, 4, 1, 2.
The following questions are to be answered by making use of the Java Collections Framework.
Implement a double-ended queue. Operations are addFront, addBack, getFront, getBack, removeFront, removeBack, and isEmpty. The get- versions get the item without removing it. The remove- versions remove the item without retrieving it. This matches the text's definition of a double-ended queue. What is the runtime for each operation?
import java.util.*;
class DoubleQueue {
List q;
public DoubleQueue () {q = new LinkedList();}
public void addFront (Object x) {q.add(0,x);}
public void addBack (Object x) {q.add(x);}
public Object getFront () {return q.get(0);}
public Object getBack () {return q.get(q.size() - 1);}
public void removeFront () {q.remove(0);}
public void removeBack () {q.remove(q.size() - 1);}
public boolean isEmpty () {return q.size() == 0;}
}We are using the LinkedList class which is a doubly-linked list. Thus, all operations take time O(1).
Write a main program that prints its arguments in sorted
order. What is the runtime if the number of arguments is n?
This is the solution given in the online tutorial: import java.util.*;
public class Sort {
public static void main(String args[]) {
List l = Arrays.asList(args);
Collections.sort(l);
System.out.println(l);
}
}
There are other possible solutions. For instance "Arrays.sort(args)"
can sort the args array directly without making it into a List. Note
though that asList doesn't do any real copying (instead it allows List
operations to occur directly on the array) and System.out.println
gives a sensible result when applied to a List, but not when applied
to an array.
import java.util.*;
class Temp {
public static void main (String[] args) {
//Test data
HashMap idToName = new HashMap(), idToSalary = new HashMap();
idToName.put(new Integer(101),"Larry");
idToName.put(new Integer(102), "Moe");
idToName.put(new Integer(103), "Curly");
idToSalary.put(new Integer(101), new Integer(500));
idToSalary.put(new Integer(102), new Integer(500));
idToSalary.put(new Integer(103), new Integer(501));
printTables( idToName, idToSalary);
}
public static void printTables (Map idToName, Map idToSalary) {
// Produce table of (name, salary) sorted by name
SortedMap tableA = new TreeMap();
for (Iterator it = idToName.keySet().iterator(); it.hasNext();) {
Integer id = (Integer) it.next();
tableA.put(idToName.get(id),idToSalary.get(id));
}
System.out.println(tableA);
// Produce a table of (name, salary) sorted by salary // We can get a set of pairs by using the entrySet() method // on tableA, but we still have to sort them. This can be // done by placing them in a list and then sorting them // using a Comparator. List tableB = new ArrayList(tableA.entrySet()); Collections.sort(tableB, new ValueComparator()); System.out.println(tableB); }
static class ValueComparator implements Comparator {
public int compare (Object x, Object y) {
Map.Entry ex = (Map.Entry) x;
Map.Entry ey = (Map.Entry) y;
// We assume that the salaries are Comparable
return ((Comparable) ex.getValue()).compareTo(ey.getValue());
}
}
}