Review Questions for Prelim II

CS211 - Fall 2000

The exam will take place at 7:30pm on Tuesday, November 14.  Please arrive a bit early so that we can begin the exam right at 7:30.  We have been assigned three rooms for this exam.  Please go to the appropriate room based on the table below.  (These are exactly the same as for Prelim I.)

The use of extra material is not permitted during the exam (i.e., no textbook, no notes, no calculator, etc.).

The exam includes material covered in lecture through November 9.  Readings corresponding to the lecture material are shown on the course web pages.  The exam is primarily on topics covered since Prelim I, but it is likely that some questions will involve material from before Prelim I.

The exam will attempt to gauge your knowledge and understanding of course concepts. You should understand the terms and concepts used in the course, but you shouldn't need to memorize the specific code given in the text or in lecture.

The review questions given here are not meant to exhaust the possible topics for exam questions.  Check the online material and consider reviewing Prelim I, the lectures, and the homework assignments.

Review Questions

Problem 1

a) Write a Java class method named append that takes two non-empty linked lists L1 and L2 as parameters, and updates the last cell of L1 so that it points to the first cell of L2.  The  method does not return anything.  The lists are built using the ListCell class given below.

b) What is the asymptotic complexity of your algorithm, expressed as a function of n₁ and n₂, where n₁ is the number of elements in L1 and n₂ is the number of elements in L2, respectively?  Justify your answer (briefly).

class ListCell {
	protected Object datum;
	protected ListCell next;
	
	public ListCell (Object x, ListCell n) {
		datum = x;
		next = n;
	}
	public Object getDatum () {
		return datum;
	}
	public ListCell getNext () {
		return next;
	}
	public void setDatum (Object x) {
		datum = x;
	}
	public void setNext (ListCell l) {
		next = l;
	}
	public String toString () {
		if (next == null) return datum.toString();
		else return datum.toString + " " + next.toString();
	}
}

Problem 2

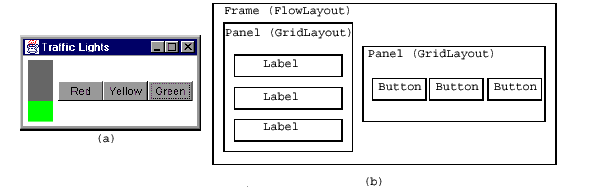
The GUI is shown in Figure (a) and the containment hierarchy is shown in Figure (b). Note that the picture is taken from an old exam (before javax.swing was released); thus, you should substitute JLabel for Label, JButton, for Button, JPanel for Panel, and JFrame for Frame.  The skeleton code is provided below. Write the method createGUI() which creates the GUI according to the containment hierarchy in Figure (b), and the method addListeners() which creates and adds the relevant listeners to the relevant sources. The user should be able to terminate the program when the “close-box” of the top-level window is clicked.

import java.io.*;
import java.awt.*;
import java.awt.event.*;
import javax.swing.*;

/**
 * Pseudo Traffic Lights
 */
public class PseudoTrafficLights extends JFrame {
	private JPanel lightsPanel;
	private JLabel redLightLabel;
	private JLabel yellowLightLabel;
	private JLabel greenLightLabel;
	private JPanel buttonsPanel;
	private JButton redLightBtn;
	private JButton yellowLightBtn;
	private JButton greenLightBtn;

// Constructor
public PseudoTrafficLights() {
	super("Traffic Lights");
	
	// Create the GUI
	createGUI();
	
	// Add the listeners to the sources
	addListeners();
	
	// Pack and show the window
	pack();		// Makes window fit tight around its contents
	setVisible(true);
}

// The main method
public static void main (String[] args) {
	new PseudoTrafficLights();
}

// Helper method to terminate the program
private void terminate() {
	dispose();
	System.exit(0);
}

// a. (13 points) Write method createGUI to set up the GUI.
private void createGUI() {



}
// b. (12 points) Write method addListeners to add listeners to the sources
private void addListeners() {



}
}

Problem 3

(a) Java Nagila, a CS211 student, implemented a bunch of algorithms and came up with the following running times as a function of input size.  Using big-O notation, write down the simples and most accurate expressions for the complexity of these algorithms.

• f(n) = 2n log(n) + 4n + 17 * log (n)
• g(n) = log(n³)

(b) You have an algorithm that runs in time O(log n).  Java Nagila claims to have found a better algorithm that runs in time O(log(n-1)).  Is either algorithm better than the other in an asymptotic sense?  Explain your answer briefly using the formal definition of big-O notation.

(c) The following method returns the i^th element of an integer list.

public static int element (List list, int i) {
	if (i == 1) return list.first();
	else return element(list.rest(), i-1);
}

What is the asymptotic time complexity of accessing the m^th element of a list using this method?  Express the complexity as a function of m and n, the length of the list.

Problem 4

Problem 5

1. Where is the smallest element in a Binary Search Tree?
2. How long does it take to insert a new element into a heap? To return the smallest thing in a min-heap? To delete the smallest thing in a min-heap? To find the largest thing in a min-heap?

Problem 6

The following picture represents a BST (Binary Search Tree).

             (22)
           /      \
       (14)        (25)
      /   \       /    \
   (11)   (16) (23)     (40)
                  \     /
                 (24) (32)

1. In what order are the nodes visited during a preorder traversal?  Inorder traversal?  Postorder traversal?
2. Show the tree that results when 15 is inserted into the tree.
3. Show the tree that results when 25 is deleted from the original tree.

Problem 7

1. Operations are Insert, DeleteMax, and DeleteMin.
   balanced tree or sorted doubly-linked list
2. You have a dictionary containing the keywords of the Pascal programming language.
   ordered array or balanced tree
3. You have a dictionary that can contain anywhere from 100 to 10,000 words.
   unordered linked-list or hash table
4. You have a large set of integers with operations insert, findMax, and deleteMax.
   unordered array or Hashtable

Problem 8

Draw a picture of the resulting hashtable (using chaining) after inserting, in order, the following words: ibex, hare, ape, bat, koala, mud, dog, carp, stork. Which cells are looked at when trying to find bird?  What is the load factor (lambda) for the hash table?

Problem 9

1. Under what conditions would you use a balanced tree instead of hashing with chaining?
2. Under what conditions would you use an unordered array instead of a balanced tree?
3. Under what conditions would you use a binary search tree instead of a heap?
4. What implementation would you use to get the best expected time for a search?
5. What implementation would you use to get the best worst-case time for a search?

Problem 10

      5
    /   \
   3     6
  / \
 1   4
  \
   2

     6
   /   \
  3     4
 / \
1   2

For each of the preceding trees, find a sequence of appropriate operations that will produce it starting from an empty tree.

 Problem 11

The following questions are to be answered by making use of the Java Collections Framework.

1. Implement a double-ended queue. Operations are addFront, addBack, getFront, getBack, removeFront, removeBack, and isEmpty. The get- versions get the item without removing it. The remove- versions remove the item without retrieving it. This matches the text's definition of a double-ended queue. What is the runtime for each operation?

2. Write a main program that prints its arguments in sorted order. What is the runtime if the number of arguments is n?

3.  Suppose you have two maps, one mapping idNumber to name and another mapping idNumber to salary. Write code to print a table giving name and salary sorted by name. Write code to print another table giving name and salary sorted by salary. You can assume that names are unique, but you should not assume that salaries are unique. How much time does it take for each of these tables?