You must work either on your own or with one partner. You may discuss background issues and general solution strategies with others, but the project you submit must be the work of just you (and your partner). If you work with a partner, you and your partner must first register as a group in CMS and then submit your work as a group.
Completing this project will help you learn about user-defined functions, nested loops, and vectors (1D arrays). Just as for the other projects in this course, your best strategy for this project is to decompose each problem into simpler pieces.
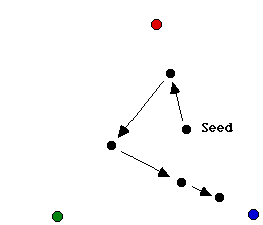
Start with an equilateral triangle T in the plane whose vertices are v1 = (0, 0), v2 = (1, 0), v3 = (1/2, sqrt(3)/2). Then pick an arbitrary point P0 in the plane and define a sequence of points {Pn} as follows: Start at P0; then choose one of the triangle�s vertices at random and let P1 be the point halfway between P0 and the chosen vertex; then again randomly choose one of the triangle�s vertices and let P2 be the point halfway between P1 and the chosen vertex. Continuing in this way yields an infinite sequence of points. The figure below illustrates the first few points of such a random sequence. We can think of this sequence as a particle moving along a random trajectory.

This process is called the chaos game because of the apparently patternless movement of the point. When we plot the points on the screen, surprisingly, a clear pattern emerges, as shown in figure below. This figure is known as the Sierpinski triangle. This question will help you appreciate the fact that simple mathematical manipulation of numbers can create somewhat artistic images.
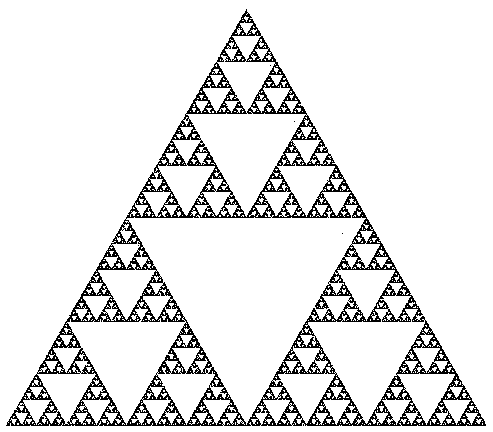
Your task is to generate the sequence of points {Pn} and use them to plot the Sierpinski triangle. You only need to generate about 38 points in order to spot this pattern, but you are allowed to plot more. You don�t need to plot the vertices v1, v2 and v3.
Write a function chaos(x,y) that returns the coordinates (two values) of the next point as described above. Write a function chaosGame(n) to draw Sierpinski's triangle using n points and your function chaos. Generate a random starting point of your choice. You can change the color and background to any color combination that you find pleasing (of course, it's a bad idea to make both colors the same). In this question you will want to use the graphics window command axis equal off to use the same scale in the x- and y-axis but hide the axes.
In 1937, Lothar Collatz conjectured that iterating the following function will always lead to the value 1 regardless of which positive integer it starts with.
f(n) = n/2 if n is even 3n + 1 if n is odd
The idea is that for any positive integer n, we can form a sequence by computing n, f(n), f(f(n)), f(f(f(n))), etc. The conjecture is that no matter where we start, we always find the value one somewhere in this sequence. This conjecture is still unresolved (although testing has been used to show it holds for integers up to a bound larger than 1016). Here are the sequences for a few small integers:
1 2 -> 1 3 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1 4 -> 2 -> 1
Write a function collatz that takes an integer as its argument and returns the vector of values produced by iterating the Collatz function on that argument (e.g., argument 4 produces the vector [4, 2, 1]). Use this function within a script that requests a number from the user and then prints the Collatz sequence for that number. Your printout should be similar to the examples given above. Your program should also report the length of the sequence; for example, the sequence above that starts at 3 has length eight; the one that starts at 4 has length three. The script should continue asking for numbers until it receives an input of 0. You might want to try your program with 27 as the starting number (the resulting sequence is of length greater than 100).
Both DNA sequences and protein sequences can be treated as character strings. For DNA there are 4 possible letters: A, C, G, and T corresponding to the 4 bases adenine, cytosine, guanine, and thymine, respectively. For proteins there are 20 possible letters: A, C, D, E, F, G, H, I, K, L, M, N, P, Q, R, S, T, V, W, Y, each representing one of the 20 amino acids.
We provide you with some sample protein and DNA data. Place the file sequenceData.mat in your Matlab current directory. Within Matlab, type "load sequenceData"; this should create two new variables within your Matlab workspace: protein and dna. Each of these variables holds a string. Variable protein holds a string representing the amino acids for the human zinc finger protein; this data was downloaded from EBI, the European Bioinformatics Institute. Variable dna holds a string representing the bases for a portion of homo sapiens chromosome one; this data was downloaded from NCBI, the National Center for Biotechnology Information.
For most proteins that appear in, say, a mouse, there are similar proteins that appear in a rat or a cat. Although such proteins accomplish the same or similar functions, they are not identical; there are substitutions, insertions, and deletions of amino acids. There are corresponding substitutions, insertions, and deletions in the portions of the DNA that encode the information a cell uses to build the proteins.
If a new protein is discovered then one way to determine the protein's likely function is to explore a database of existing proteins to find one with a similar sequence of letters. The fact that there are substitutions, insertions, and deletions can make this search difficult.
For this problem, you are to write a simple tool for finding substrings similar to a query string within a longer data string. Solving this problem in full generality requires the use of Dynamic Programming, an algorithm design technique that is studied in CS482; thus, for CS100M, we restrict our definition of similar to allow just substitutions---no insertions and no deletions.
Write a function called partialMatches. Its arguments should be (1) a data string, (2) a query string, and (3) a number indicating the maximum number of substitutions (i.e., single-letter mismatches) allowed. The function should return a vector with one entry for each legal match found; each such entry should indicate the location of the start of the match. For example, partialMatches('mathematics','mat',0) should return [1, 6] and partialMatches('mathematics','mat',3) should return [1,2,3,4,5,6,7,8,9]. For another example, partialMatches('mathematics','matter', k) should return the zero-length vector for k = 0 and 1, and should return the vector [1] for k = 2. You should not need to use any of the Matlab string functions; in particular, do not use findstr or strrep or any of the functions related to regular expressions. The goal here is to practice working with vectors rather than to look up string functions in the Matlab documentation.
Write an additional function, plotMatchData, that uses your function partialMatches to explore the protein sequence and the DNA sequence that can be loaded from sequenceData.mat as explained above. The function plotMatchData(data,query) is to create a plot showing the number of matches found as a function of the maximum number of substitutions (mismatches) allowed. You should plot the data for 0, 1, 2, or 3 mismatches. Try your function on plotMatchData(protein,'WEAVE') and on plotMatchData(dna,'GAGACAT').