Assignment A4   CS100J    Fall 2006    Due about 19 October (see CMS for deadline)

This assignment introduces you to graphics. You will write procedures that draw a square and two circles, spirals, bouncing balls, and a "Koch snowflake" in a JFrame. You may work with one other person. If you do so, please form a group for this assignment on the CMS WELL BEFORE YOU SUBMIT YOUR FILES. You will not use a JUnit testing program because you will be looking at visual output (graphics) to determine correctnesss. You must use javadoc comments —before submitting the assignment, click the javadoc button and look carefully at the specs produced. At the end of this document, we tell you what to submit.

Download file Turtle.class (from here or from the course website) and put it in its own directory. Also download the javadoc specs for this class, unzip it, and store it somewhere on your hard drive. You will be using these specs, and not the source code itself, to learn how to deal with turtles.

A Turtle is a pen of a certain color at a pixel (x, y) that is pointing in some direction, given by an angle (0 degrees is to the right, or east; 90 degrees, north; 180 degrees, west; and 270 degrees, south). When the turtle is moved to another spot using procedure move, a line is drawn if the pen is currently "down" and nothing is drawn if the pen is "up". The pen is initially black, but its color, of class java.awt.Color, can be changed. A footnote on page 1.5 of the ProgramLive CD contains information about class Color.

Study the specifications of methods in class Turtle (the javadoc files). Here are some important points:

In DrJava, create another file with the following class in it (copy and paste; then use the indent-line feature of DrJava to indent the lines appropriately) and save it in the same directory with file Turtle.class.

import java.awt.*;
/** Assignment A4: using a Turtle */
public class MyTurtle extends Turtle {
/** Draw a black line 30 pixels to the right (east) and then
a red line 35 pixels down (south). */
public void drawTwo() {
move(30); // draw a line 30 pixels to the right (east)
addAngle(270); // add 270 degrees to the angle
setColor(Color.red);
move(35);
}
}

We give you one method in this class as an example of how graphics works. After compiling class MyTurtle, in DrJava's interaction pane, create an instance of class MyTurtle and then execute a call on this method and see what happens. A JFrame should be created and two lines should be drawn on it.

In the interactions pane (or in a method in class MyTurtle), draw some lines, rectangles, circles, etc, to familiarize yourself with class Turtle. After that, perform the tasks given below. Put a precise and complete specification on any method you write as a javadoc comment —many points will be deducted if you don't. The specification should allow anyone to know precisely what a call on the method does. It must mention all parameters and say what they are for. Look at your javadoc specs to make sure they are appropriate. As usual, your methods must have our names, exactly, and have the same parameters.

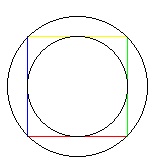
Task 1. Write a procedure drawSquareCircles(int e) that does the following (see the diagram to the right).

(1) At the current turtle position but facing east (you have to make it face east), draw a square of side length e to the right and upward whose side l. The first line should be red, the second, green; the third, yellow; and the fourth, blue.

Next, draw two circles, using the color being used at the start of the method. The first circle is inside the square and touches the square at the midpoints of its lines. The second circle is outside the square and touches the square at the endpoints of its lines.

After drawing the square and circles, place the turtle in its initial position, facing in its initial direction.

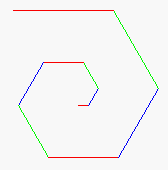
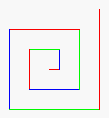
Task 2: Draw a spiral. The first picture to the right is done by drawing 10 lines. The first line has length 5; the second, 10; the third, 15, etc. After each line, 90 degrees is added to the angle. The second diagram to the right shows a similar spiral but with 60 degrees added to the angle after each line.

Write a procedure spiral(int n, int ang, int e, int msec); that draws n lines, adding angle ang after each one. Line 1 is e pixels long, line 2 is 2*e pixels long, ..., line i is i*e pixels long. The lines alternate among red, blue, and green, with the first one being red. Pause msec milliseconds after drawing each line.

Then write a procedure spiralm(int n, int a, int d, int sec) that does the same thing as spiral, but first it:

  1. Sets the size of the graphics panel as large as possible (use procedure setPanelSize in class Turtle).
  2. Places the turtle in the middle of the window facing east.

When you first test your method, use 5 for d and 0 for sec. Try different angles, like 90 degrees, 92 degrees, 88 degrees, etc. You can also use msec = 500 or msec =1000 in order to see the lines drawn one at a time.

You will be amazed at what method spiral does. Find out by trying these calls, assuming that x is an instance of MyTurtle (use procedure clear(), to erase the panel before each one):

x.spiralm(500, 90, 1, 0);       x.spiralm(500, 135, 1, 0);        x.spiralm(500, 60, 1, 0);     
x.spiralm(500, 121, 1, 0);     x.spiralm(500, 89, 1, 0);          x.spiralm(500, 150, 1, 0);
x.spiralm(500, 120, 1, 0);     x.spiralm(500, 119, 1, 0);

Task 3: Bouncing balls. Procedure Turtle.fillCircle draws a disk —a filled-in circle. You can use this procedure to draw a bouncing ball. Suppose the ball is at some position (x, y). To make it look like the ball is moving, repeat the following process over and over again:

1. Pause for 100 milliseconds.
2. Move the ball: (1) Draw the ball at its current position using color white, thus erasing it, (2) change the position of the turtle, and (3) draw the ball in its own color.

(a) Start a new .java file for class Ball, which extends MyTurtle. This class needs three (private) double fields: radius gives the radius of the ball and variables vx and vy describe the speed of the ball —when the ball is moved, it moves vx pixels in the horizontal direction and vy pixels in the vertical direction. Write getter methods for these fields.

(b) Write a constructor Ball(x, y, c, r, vx, vy) that initializes a new Ball folder in which the center of the ball is at (x, y), its radius is r, its color is c, and its speed is (vx, vy). THE TYPE OF c IS Color. Class Color is in package java.awt. You know the constructor works properly when you see the ball in the panel.

To make things easier, alsowrite a constructor Ball(vx, vy, r) that creates a black ball at the midpoint of the panel with speed (vx, vy) and radius r. Then, create several balls, with different starting points, radii, and colors, before going on to the next step.

(c) Write a procedure moveOnce() that moves the ball once, as given by the speed (vx, vy) of the ball; whenever the ball bounces off a wall (or two walls at the same time), increase its radius by 1 pixel. Follow these directions:

  1. To erase the ball, you have to draw it with a white pen. Then you have to move the turtle. And finally you have to draw the ball in its original color. So, you have to remember the original color. Have a local variable originalColor to contain the original color and, after drawing the ball white, set the turtle color back to the value of variable originalColor.
  2. After moving the ball, if the ball just touches or goes partially over the top of the panel, then negate the y-coordinate speed (using vy= – vy;) so that the next move will be in the opposite direction. You have to do the same kind of thing for the other three walls. Note that if the ball hits two adjacent boundaries at the same time, the radius should be increased by only 1.

Test method moveOnce() carefully. Here is an example of how to test it. In the interactions pane, create a ball d of radius 40 that starts in the middle of the panel and has velocity (0, –30). Then, repeatedly execute d.moveBallOnce() and watch what happens. Makes sure that it bounces properly off the top and bottom walls. Then do the same kind of test for the left and right walls.

Note that if a ball is very big —its diameter is more that 1/2 the height, for example, it will bounce off the top and bottom in such a manner that it doesn't look like it is bouncing very well. Do not concern yourself with this situation.

(d) Write a procedure bouncing() that puts the ball perpetually in motion. Its body should be a loop that does not terminate and that has a repetend that (1) moves the ball once and then (2) pauses for 100 milliseconds. In the interactions pane, create a new Ball d, call d.Bouncing();, and watch the ball move. Stop this execution by hitting the DrJava reset button.

Now change procedure bouncing (and its specification) so that it stops (with a return statement) when the diameter of the ball is bigger than half the width or half the height of the panel.

(e) Write a static method bouncing(Ball b1, Ball b2) that puts both balls b1 and b2 in motion forever but stops if one of them becomes too big, as in part (d).

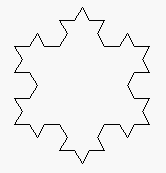
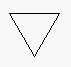Task 4. Koch snowflakes. Directly to the right is a triangle. It is called a "Koch snowflake" of depth 0. Replacing each line of this Koch snowflake by four lines, as drawn in the second diagram, yields the Koch snowflake of depth 1, which is the third figure. Replacing each of the lines of this Koch snowflake by the same four lines yields the Koch snowflake of depth 2 shown on the extreme right. We can continue this to any depth.

This is a neat use of recursion! That's what you will do here. First, copy the two specs given below into your class MyTurtle.

/** Make sure that the graphics panel is as large as possible in the window. Clear the window, place the turtle facing east at position (width/5, height/3). Then draw a Koch snowflake of depth d with line segment length F. Pause s milliseconds after drawing each line segment. Precondition: d ≥ 0*/
public void Koch(int d, double F, int s) {}

/** Draw a KochD snowflake of depth d with the current turtle. Parameters d, F, and s are as in procedure Koch.
      Precondition: d ≥ 0 */
public void KochD(int d, double F, int s) {}

Procedure Koch is the easiest. First, call setPanelSize() in order make the graphics panel as large as possible within the window. Then, call procedure moveTo to move the turtle as in the specification (and make the turtle face east). Finally, draw as shown below.

The commands to be placed in Koch and KochD are described by the following two patterns:

Here's how to interpret each of them. Each symbol is a command to do something, as follows.

F: Base case: d = 0. Draw a line of length F
F: Recursive case: d ≠ 0. Call KochD(d-1, F, s).
+: add 60 degrees to the turtle's angle.
–: subtract 60 degree from the turtle's angle.

So, the patterns are simply a simple, terse, way of describing what each of the method bodies should do. Such a system of patterns is called a "Lindenmayer System", after Aristid Lindenmayer, who co-authored a book titled The Algorithmic Beauty of Plants (Springer Verlag, 1990).

Your task, then, is to complete the bodies of Koch and KochD according to the patterns given above for them —and test and debug until they are correct. The following hint may help make things easier. In each procedure, first test whether d is 0; if it is, then carry out all the commands under that assumption and return. Then, carry out all the commands under the assumption that d > 0.

Task 5! Do something of your choice. It should be non-trivial, of course. Make sure you say what it does in its specification. Place it in class Ball. We don't care what your procedure does. You could draw a face whose size depends on a parameter. You could make some interesting design with a few stars. You could write a method with a parameter n that draws an n-pointed star. You could have two bouncing balls change direction when they collide --when they occupy the same space. (To have more than one ball move perpetually, you need a method with an infinite loop that moves all the balls one step and then pauses.) You could have more bouncing balls; when two collide, the smaller one blows up (goes completely off the screen). You could change the initial color of the panel to something other than white and then put a ball in motion, so that you see the path it takes. How about placing some rectangles at the top of the panel; when a ball hits them, the rectangle disappears and the ball changes direction. You could find some other interesting recursive procedure that draws something. Use your imagination. We will make the most interesting procedures available on the course website.

What to submit. Before you submit, make sure classes MyTurtle and Ball are indented properly. Then, click the javadoc button and look at the API specs produced by that click. Check each method spec in MyTurtle and Ball to be sure that exactly what a call on the method does can be determined from the spec. If you don't do this, you will lose a lot of points.

Submit files MyTurtle.java and Ball.java.