Investigation of Spherical Packings via Simulated Annealing

I. Overview of the Project

The goal of this project is to investigate the following features of systems modeled as discrete polygons:

- Optimal Packings

- Simulated Annealing

- Convex Hulls

- Deformations of the System

The objective is to build a model that can simulate real systems in nature, and in particular a model for lung inflation.

II. Packings

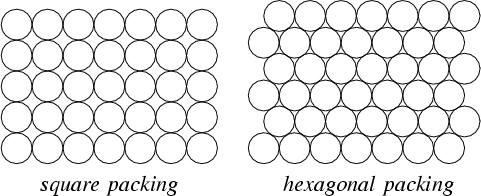
One of the challenges of modeling is to be able to consistently produce optimal configurations for a system quickly and accurately. In particular, the model under development must optimize for "low energy" states that should be close to the optimal packing for a configuration of circles or spheres. The pictures below illustrate two packing methods for circles in the plane. The packing on the right has been shown to be optimal for a collection of identical circles. Other packings are not so well known.

from Eric W. Weisstein. "Circle Packing." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/CirclePacking.html

For packings involving circles of various sizes, proven optimal packings are much more difficult to find, and in three dimensions, the problem is only magnified. A goal of the project is to be able to produce near optimal configurations for a variety of different circles / spheres by using a technique known as simulated annealing.

III. Simulated Annealing

By using a temperature schedule and Markov chains, the simulated annealing method that has been implemented weights both the length of the convex hull and the volume it encloses when calculating the energy of a particular state. An attraction mimicking gravity is implemented in order to improve packing and the realism of the model. A surprising conclusion from this stage of the research was that the annealing algorithm benefited substantially from allowing the spheres to vary only along one directional vector at a time (i.e. only the x direction, y direction, or z direction) instead of moving completely randomly at each stage of the annealing.

IV. Convex Hulls

The current implementation supports a divide and conquer convex hull algorithm that is modified to suit the special case of this particular problem. Specifically, in 2D, the algorithm uses the fact that the circles are already convex hulls themselves in order to skip directly to the merging stage of the algorithm. The 3D convex Hull algorithm is still under development.

V. People

This project was programmed by Nicholas Ruozzi (CS '06) as an undergraduate research project under the direction and support of Graeme Bailey. It is to be presented at BOOM 2004.

VI. Downloads

(Coming Soon)

References:

Preparata, F. and Shamos, M. Computational Geometry An Introduction. New York, New York: Springer-Verlag, 1985.

Press, W.; Vetterling, W.; Flannery, B.; Teukolsky, S. Numerical Recipes in C: The Art of Scientific Computing. Cambridge University Press, 1992

Weisstein, Eric W. "Circle Packing." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/CirclePacking.html

Logo: Weisstein, Eric W. "Hexagonal Close Packing." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/HexagonalClosePacking.htm

Links: