Strategy

As each new tetrad appears at the top of the playing field, the computer needs to determine its best final resting place. Fortunately, the search space for tetrad placement, shown below in Figure 3, is small enough to be completely evaluated in a short amount of time. In the worst case, the current tetrad can rotate to four distinct orientations. For each of these orientations, the tetrad can be moved to a maximum of 10 different horizontal positions. From each of these positions, once dropped, the piece could be slid left, not moved, or slid right. This worst case scenario leads to 4 x 10 x 3 = 120 final positions. This is considered the shallow search and stops at level 3 in the tree below. Accounting for the next tetrad (in the Next Tetrad Preview window) constitutes the deep search - traversing the tree in the blue oval below with each of the maximum 120 nodes at level 3 connecting to the same tree structure for the next tetrad. Thus, the tree for the deep search has a maximum of 120² = 14,400 leaves.

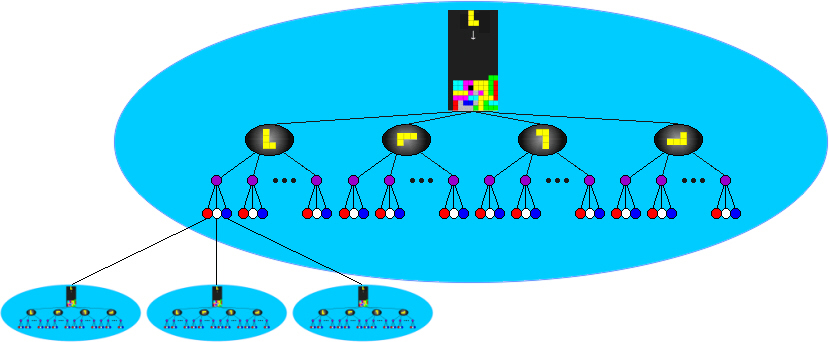
Figure 3. Search space for placement of a tetrad with 4 possible orientations. The shallow search only traverses the tree in the large blue oval. The deep search - optimizing for the current and next tetrads - appends an entire tree structure onto each of the leaves. (Only 3 additions are shown due to space constraints.)

The computer player conducts a Depth-First Search on the tree. At each leaf, it calculates an evaluation function described on the "Evaluation Function" page. The leaf whose function returns the highest value corresponds to the best place to deposit the tetrad. Fortunately, the tree is structured in terms of a sequence of moves, so the computer automatically knows what moves to make to put the tetrad in the optimal spot. Unless the user disables the Next Tetrad Preview, the computer executes a deep search for every tetrad as long as no filled square (a square that has a non-black color, excluding the squares that make up the currently dropping tetrad) has a height ³ 14. Whenever the filled squares do reach this high, it executes a shallow search for the sake of quicker execution.

The key to a fast search time lies in significant pruning done to the tree. Only 3 of the 7 tetrads have four distinct orientations. Three of them have 2 orientations, and the blue square tetrad only has one. This significantly reduces the size of the search space. In addition, the number of possible horizontal placements differs from tetrad to tetrad and orientation to orientation. The search always visits the minimum number of nodes that covers all possible moves. For further pruning, sliding to the left or right at the end of the move sequence is only considered if there is a hole (a blank square that has at least one filled square above it in the same column) in the playing field and if the slide results in a position in which the tetrad would be at rest (and not floating in the air). This last sort of pruning only makes a significant difference for the deep search, since it only trims off leaves for the shallow search.

Notes:

· The tree structure covers all possible reasonable moves during reasonable game play. It doesn't allow for moves such as sliding under a shelf of squares and rotating underneath, or sliding into a notch in mid-air, but playing field states for which these types of moves should be done does not tend to occur during rational play. · Once the deep search is completed, the computer has an optimal sequence of moves for the current tetrad and the next tetrad. However, only the moves for the current tetrad are executed. Once the next tetrad appears on the screen, a new deep search is conducted to determine if there is now a better sequence of moves for this now current tetrad in light of the new next tetrad.