This page has moved to https://iss.oden.utexas.edu/. This page is kept for archival purposes only.

 

Contents People Research Program Analysis Memory Hierarchy Optimizations Next-generation Generic Programming Irregular Applications Program Representation Compiling for Parallel Machines Instruction-level Parallelism Functional Languages with Logic Variables Software List of Papers Copyright ©Cornell University

High Performance Systems Software People Faculty Keshav Pingali Researchers Paul Stodghill Graduate Students Nawaaz Ahmed James Ezick Nikolay Mateev Vijay Menon Research Program Analysis Algorithmic breakthroughs made by our project have enabled us to design fast and practical algorithms for several fundamental program analysis problems.  Fractal symbolic analysis is a new analysis technique for use in restructuring compilers to verify legality of program transformations. It combines the power of symbolic program analysis with the tractability of dependence analysis, and it permits restructuring of  far more complex codes than current technology can handle.  We have developed an intermediate representation called the Abstract Matrix Form (AMF) and we have used it to extract matrix operations from low-level code. This led us to a new approach to optimizing programs in languages like MATLAB. Optimal algorithm for computing control dependence: This algorithm computes a data structure called APT which answers queries for control dependence successors and predecessors in time proportional to output size. Preprocessing time is O(|E|). This is an improvement over previous algorithms which took O(|E||V|) space and time (|E| and |V| are the number of edges and nodes in the control flow graph). A sample implementation of the APT data structure for computing control dependence, as described in the TOPLAS paper of Pingali and Bilardi can be found here . It implements cd, conds and cdeq queries. Optimal algorithms for determining control regions:  The problem is to compute all nodes in a control flow graph that have the same control dependence predecessors as a given node. We have developed two very different algorithms for this problem. One of the algorithms requires computing the postdominator tree of the control flow graph, and requires O(|E|) space and time. The other algorithm is based on cycle-equivalence, and it too requires O(|E|) time. These are improvements over previous algorithms which required O(|E||V|) time. Optimal algorithm for weak control dependence: For program verification, Clarke and Podgurski have proposed a variation of control dependence called weak control dependence. Their algorithm for computing this relation takes O(|E|3) time. Our algorithm computes this relation in O(|E|) time.  Generalized control dependence: We have defined a generalized control dependence that subsumes both standard control dependence and weak control dependence, and shown how to compute generalized control dependence predecessors, successors and regions optimally.  This paper describes how to compute interprocedural dominators and interprocedural control dependence in O(|E||V|) time. O(|E|) time algorithm to compute the SSA form of programs: This algorithm performs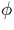$\phi$-function placement for computing the Static Single-Assignment (SSA) form of programs in O(|E|) time. On the SPEC benchmarks, this algorithm runs 5 times faster than other O(|E|) time algorithms for this problem. Memory Hierarchy Optimizations  The performance of most codes on fast machines is limited by the so-called memory wall. Processors run much faster than memory, so if a code touches large amounts of data, the processor spends most of its cycles waiting for memory requests to complete rather than in doing computations. Many of these codes can benefit from restructuring to improve locality of reference. It is tedious to do this restructuring by hand, so automatic restructuring technology  for accomplishing this goal is highly advantageous.  Our group is a world-leader in the area of compiler technology for memory hierarchy optimization. Compiler product-lines of companies like Intel, Hewlett-Packard and Silicon Graphics incorporate technology developed by our group.   Imperfectly-nested loop transformations: Imperfectly-nested loops are loops that have statements nested in some but not all of the loops in the loop nest.  We have developed a systematic approach to tiling imperfectly-nested loops . We designed a theory of imperfectly-nested loop transformations for locality enhancement, and showed its effectiveness of codes of practical importance. Automatic generation of divide-and-conquer codes from iterative codes An intriguing feature of divide-and-conquer algorithms is that they should run well on machines with multiple levels of memory hierarchy without the need for blocking since each successive divide step generates subproblems that touch  smaller amounts of data. We have shown how divide-and-conquer codes can be generated automatically from iterative versions of the same algorithm. Data-centric Blocking for Memory Hierarchies: We have developed a novel compilation approach called data-shackling to address some of the problems of generating blocked numerical codes automatically from point codes.  An evaluation of data-shackling and tiling within the SGI MIPSPro compiler demonstrates the superiority of data-shackling. Silicon Graphics is using data-centric blocking to do blocking for caches in their entire compiler product line. Induprakas Kodukula's thesis describes the aggregation of this work. Transformations for perfectly nested loops: We have invented a loop transformation framework based on integer non-singular matrices. This framework subsumes loop permutation, skewing, scaling and reversal. We implemented the LAMBDA loop transformation toolkit based on this framework. A paper on LAMBDA won the best paper award at ASPLOS V. We used LAMBDA to enhance parallelism and locality of reference in perfectly nested loops. A detailed description of the experiments with LAMBDA can be found in our TOCS paper. The theory behind LAMBDA is described in Wei Li's PhD thesis. Hewlett-Packard has adopted the technology in LAMBDA for performing loop transformations in its entire compiler product line. Intel has recently licensed the LAMBDA toolkit for use in Merced compilers. Transformations for imperfectly nested loops: We have extended the theory behind LAMBDA to handle imperfectly nested loop transformations like distribution and fusion. This approach has been implemented in the MU toolkit. A paper on MU was nominated for the Best Student Paper award at Supercomputing '96. Next-generation Generic Programming     We are implementing a novel generic programming system for simplifying the job of writing computational science codes that use sparse matrices. This system uses two API's; a high-level one for the algorithm designer and low-level one for the sparse matrix format implementor. Restructuring compiler technology is used to translate programs written in the high-level API into those that use the low-level API.      One view of this system is that it is an aspect-oriented system which uses restructuring compiler technology to weave sparse format aspects into the functional specification of the algorithm.    The API's in the generic programming system is described in this paper. An elegant restructuring compiler technology for translating between these API's is described in this paper. This is the most up-to-date description of the compiler technology. This  paper  introduces the data-centric code generation model that is the foundation of the low-level API, and shows how it can be viewed abstractly as the optimization of certain relational queries generated from the user program. A paper in SIAM '97 discusses how sparse matrix formats can be described to the compiler for use in optimization and code generation. A paper in Supercomputing '97 shows how the relational approach can be used to generate parallel sparse matrix code. A unified approach to compiling both dense and sparse matrix programs can be found here. Paul Stodghill's PhD thesis contains a detailed description of compiling sparse codes for sequential machines. Vladimir Kotlyar's PhD thesis contains details on how to extend the sequential techniques to parallel codes, and to codes that are imperfectly-nested and have dependencies. Slides from Kotlyar's job talk summarize the work that he did for his thesis.   Irregular Applications Our project has developed parallel algorithms for several unstructured and semi-structured applications including Structured Adaptive Mesh Refinement (SAMR) and circuit simulation. SAMR is used to simulate physical phenomena like shock wave propagation for which efficient simulation requires a grid whose coarseness varies with time. We have also participated in the development of a parallel MATLAB environment called MultiMATLAB.   SAMR: A paper in ICS '97 describes compiler and runtime support for SAMR. A more applications-oriented paper can be found here.  MultiMATLAB: Vijay Menon has worked with Anne Trefethen in the implementation of a parallel MATLAB system called MultiMATLAB. Circuit Simulation: We have developed a new technique for compiled zero delay logic simulation which partitions the circuit into fanout free regions (FFRs), transforms each region into a linear sized BDD (binary decision diagram), and converts each BDD into executable code. On standard benchmarks, we observed a performance improvement of upto 67%. Program Representation The dependence flow graph(DFG) is an intermediate program representation that unifies control flow and dataflow information. It has an operational semantics based on the dataflow model of computation. It can be used for performing standard dataflow analyses, and for program debugging using slicing.   An introduction to the dependence flow graph (DFG) and its operational semantics can be found in our POPL '91 paper. Algorithms for contructing the DFG can be found in our JPDC paper. We have also explored an extension of the DFG that incorporates distance and direction information. Micah Beck's PhD thesis has a detailed description of the construction of DFGs. Richard Johnson's PhD thesis contains a detailed discussion of the DFG and a related data structure called the Quick Propagation Graph (QPG), and their use for program analyses. IBM's VLIW compiler uses the DFG as its internal representation.  Compiling for Parallel Machines Our project implemented one of the first compilers that generated message-passing code from sequential shared-memory programs with data distribution directives. We introduced several concepts like runtime resolution and the owner-computes rule that have become part of the standard terminology in this area.   A survey paper on parallel languages can be found here. Automatic alignment: We have developed an algorithm to compute data and computation alignment automatically by reducing the alignment problem to the standard problem of finding a basis for the null space of a matrix. Code Generation Techniques: A paper in PLDI'89 described a code generation strategy based on runtime resolution and the owner-computes rule. We implemented a compiler, based on this approach, to translate programs in the dataflow language Id Nouveau into message-passing code for the Intel iPSC/2. A summary can be found in our TPDS paper. A performance analysis of the code generated by our compiler for the SIMPLE benchmark from Los Alamos can be found here. Anne Rogers' PhD thesis has a complete description.  Instruction-level Parallelism Our project has developed algorithms for software pipelining. We have also collaborated with Stamatis Vassiliadis from IBM Glendale Labs in the design of superscalar processor that implements register renaming, dynamic speculation and precise interrupts in hardware.   We have developed a software pipelining scheme called bidirectional slack scheduling which generates loop code with minimal register pressure without sacrificing the loop's minimum execution time. We have collaborated with Stamatis Vassiliadis of IBM Glendale Labs in the design of a superscalar processor that implements register renaming, dynamic speculation and precise interrupts in hardware. A detailed discussion of the superscalar processor and related software issues can be found in Mayan Moudgill's PhD thesis. Functional Languages with Logic Variables The addition of logic variables to functional languages gives the programmer novel and powerful tools such as incremental definition of data structures through constraint intersection. Id Nouveau is one such language for which we have given a formal semantic account using the notion of closure operators on a Scott domain. We have also used logic variables to model demand propagation in the implementation of lazy functional languages, and we have explored the use of accumulators, which are generalized logic variables. Language Constructs: In joint work with Arvind and Rishiyur Nikhil, a weak form of logic variable called I-structures was added to the dataflow language Id. This work was the origin of the language Id Nouveau. With K. Ekanadham of IBM Hawthorne, we generalized the idea of a logic variable to obtain a construct called the accumulator.  Semantics of Id Nouveau: We have used the notion of closure operators on a Scott domain to give a formal semantics of first-order Id Nouveau. This semantics is fully abstract with respect to a Plotkin-style operational semantics for this language. A conference version of this paper was published in the Symposium on Logic in Computer Science (LICS) '87. The first-order semantics has been extended to give a semantics for higher-order Id Nouveau. Radha Jagadeesan's PhD thesis contains a detailed account of the semantics of Id Nouveau. Lazy Evaluation: We have shown that demand propagation in lazy functional languages can be modeled using logic variables. This makes it possible to expose the process of demand propagation to the compiler of a lazy language, permitting optimization of demand propagation code.  Software The following packages are available for downloading. A sample implementation of the APT data structure for computing control dependence, as described in the TOPLAS paper of Pingali and Bilardi can be found here. It implements cd, conds and cdeq queries. List of Papers Nikolay Mateev, Keshav Pingali, Paul Stodghill, and Vladimir Kotlyar. Next-generation Generic Programming and its Application to Sparse Matrix Computations. In International Conference on Supercomputing, 2000.   Nawaaz Ahmed, Nikolay Mateev, and Keshav Pingali. Synthesizing Transformations for Locality Enhancement of Imperfectly-nested Loop Nests. In International Conference on Supercomputing, 2000.   Nikolay Mateev, Vijay Menon, and Keshav Pingali. Fractal Symbolic Analysis for Program Transformations. Technical Report TR2000-1781, Cornell Computer Science Department, 2000.    Nawaaz Ahmed, Nikolay Mateev, and Keshav Pingali. Tiling Imperfectly-nested Loop Nests. Technical Report TR2000-1782, Cornell Computer Science Department, 2000.    Nawaaz Ahmed, Nikolay Mateev, Keshav Pingali, and Paul Stodghill. Compiling Imperfectly-nested Sparse Matrix Codes with Dependences. Technical Report TR2000-1788, Cornell Computer Science Department, 2000.    James Ezick, Gianfranco Bilardi, and Keshav Pingali. Efficient Computation of Interprocedural Control Dependence. Submitted for publication, 2000.    Gianfranco Bilardi and Keshav Pingali. The Static Single Assignment Form and its Computation. Submitted for publication, 2000.    Nawaaz Ahmed and Keshav Pingali. Automatic Generation of Block-recursive Codes. Submitted for publication, 2000.    Nikolay Mateev, Vijay Menon, and Keshav Pingali. Left to Right and vice versa: Applying Fractal Symbolic Analysis to Restructuring Linear Algebra Codes. Submitted for publication, 2000.    Vijay Menon and Keshav Pingali. A Case for Source-Level Transformations in MATLAB. In The 2nd Conference on Domain-Specific Languages, 1999.   Vijay Menon and Keshav Pingali. High-Level Semantic Optimization of Numerical Codes. In International Conference on Supercomputing, 1999.   Induprakas Kodukula, Keshav Pingali, Robert Cox, and Dror Maydan. An experimental evaluation of tiling and shackling for memory hierarchy management. In International Conference on Supercomputing, 1999.   Keshav Pingali. Parallel and Vector Programming Languages. In Wiley Encyclopedia of Electrical and Electronics Engineering, vol.15, 1999.   Vladimir Kotlyar. Relational Query Processing Approach to Compiling Sparse Matrix Codes. slides from a talk, 1999.   Vladimir Kotlyar. Relational Algebraic Techniques for the Synthesis of Sparse Matrix Programs. PhD thesis, Cornell University, 1999.   Induprakas Kodukula. Data-centric Compilation. Ph.D. Thesis, Cornell Universiry. Vladimir Kotlyar, Keshav Pingali, and Paul Stodghill. Compiling Parallel Code for Sparse Matrix Applications. In Supercomputing, November 1997.   Vijay Menon and Anne E. Trefethen. MultiMATLAB: Integrating MATLAB with High-Performance Parallel Computing. In Supercomputing, November 1997.   Induprakas Kodukula, Nawaaz Ahmed, and Keshav Pingali. Data-centric Multi-level Blocking. In Programming Language Design and Implementation, June 1997.   Keshav Pingali and Gianfranco Bilardi. Optimal Control Dependence and the Roman Chariots Problem. ACM Transactions on Programming Languages and Systems (TOPLAS), 19(3), May 1997.   Nikos Chrisochoides, Induprakas Kodukula, and Keshav Pingali. Compiler and run-time support for semi-structured applications. In International Conference on Supercomputing, 1997.   Nikos Chrisochoides, Induprakas Kodukula, and Keshav Pingali. Compiler support for easing the programmer's burden. In Workshop on Structured Adaptive Mesh Refinement Grid Methods, 1997.   Nikos Chrisochoides, Induprakas Kodukula, and Keshav Pingali. Data Movement and Control Substrate for network-based Parallel Scientific Computing. In CANPC '97, 1997.   Vladimir Kotlyar, Keshav Pingali, and Paul Stodghill. Compiling Parallel Sparse Code for User-Defined Data Structures. In SIAM Conference on Parallel Processing for Scientific Computing, volume 8, 1997.   Vladimir Kotlyar, Keshav Pingali, and Paul Stodghill. A Relational Approach to Sparse Matrix Compilation. In EuroPar, 1997.   Vladimir Kotlyar, Keshav Pingali, and Paul Stodghill. Unified framework for sparse and dense SPMD code generation. Technical Report 97-1625, Cornell Computer Science Department, 1997.   Paul Stodghill. A Relational Approach to the Automatic Generation of Sequential Sparse Matrix Codes. PhD thesis, Cornell University, 1997.   Induprakas Kodukula and Keshav Pingali. Transformations of Imperfectly Nested Loops. In Supercomputing, November 1996.   Gianfranco Bilardi and Keshav Pingali. A Framework for Generalized Control Dependence. In Programming Language Design and Implementation. SIGPLAN, June 1996.   Sudeep Gupta and Keshav Pingali. Fast Compiled Logic Simulation Using Linear BDDs. Technical Report TR95-1522, Cornell Computer Science Department, 1995.   Vladimir Kotlyar, Keshav Pingali, and Paul Stodghill. Automatic Parallelization of the Conjugate Gradient Algorithm. In Languages and Compilers for Parallel Computers, volume 8, 1995.   Keshav Pingali and Gianfranco Bilardi. APT: A Data Structure for Optimal Control Dependence Computation. In Programming Language Design and Implementation. SIGPLAN, 1995.   Wei Li and Keshav Pingali. The LAMBDA Loop Transformation Toolkit. Technical Report TR94-1431, Cornell Computer Science Department, 1994.   Mayan Moudgill. Implementing and Exploiting Static Speculation on Multiple Instruction Issue Processors. PhD thesis, Cornell University, August 1994.   Vladimir Kotlyar, Induprakas Kodukula, Keshav Pingali, and Paul Stodghill. Solving Alignment Using Elementary Linear Algebra. In Languages and Compilers for Parallel Computers, volume 7, 1994.   Richard Johnson, David Pearson, and Keshav Pingali. The Program Structure Tree: Computing Control Regions in Linear Time. In Programming Language Design and Implementation. SIGPLAN, 1994.   Richard Johnson. Efficient Program Analysis Using Dependence Flow Graphs. PhD thesis, Cornell University, 1994.   Wei Li. Compiling for NUMA Parallel Machines. PhD thesis, Cornell University, 1994.   Richard Huff. Lifetime-Sensitive Modulo Scheduling. In Programming Language Design and Implementation. SIGPLAN, 1993.   Richard Johnson and Keshav Pingali. Dependence Based Program Analysis. In Programming Language Design and Implementation. SIGPLAN, 1993.   Mayan Moudgill, Keshav Pingali, and Stamatis Vassiliadis. Register Renaming and Dynamic Speculation: an Alternative Approach. In MICRO, 1993.   Radha Jagadeesan and Keshav Pingali. Abstract Semantics for a Higher-Order Functional Language with Logic Variables. In Principles of Programming Languages, volume 19, 1992. Available as Cornell CS TR91-1220.   Wei Li and Keshav Pingali. Access Normalization: Loop Restructuring for NUMA Compilers. ACM Transactions on Computer Systems, 11(4), November 1993.   Wei Li and Keshav Pingali. Access Normalization: Loop Restructuring for NUMA Computers. In Architectural Support for Programming Languages and Operating Systems, volume 5, 1992. An extended version appeared in ACM Transactions on Computer Systems.   Richard Johnson, Wei Li, and Keshav Pingali. An Executable Representation of Distance and Direction. In Languages and Compilers for Parallel Computers, volume 4, 1991.   Radha Jagadeesan, Keshav Pingali, and Prakash Panagaden. A Fully Abstract Semantics for a Functional Langauge with Logic Variables. ACM Transactions on Programming Languages and Systems, 13(4), October 1991. Available as Cornell CS TR89-969.   Radha Jagadeesan. Investigations into Abstractions and Concurrency. PhD thesis, August 1991.   Wei Li and Keshav Pingali. A Singular Loop Transformation Framework Based on Nonsingular Matrices. International Journal of Parallel Processing, 22(2), April 1991.   Micah Beck, Richard Johnson, and Keshav Pingali. From Control Flow to Data Flow. Journal of Parallel and Distributed Computing, 12, 1991.   Keshav Pingali, Micah Beck, Richard Johnson, Mayan Moudgill, and Paul Stodghill. Dependence Flow Graphs: An Algebraic Approach to Program Dependencies. In Principles of Programming Languages, volume 18. SIGPLAN, 1991.   Anne Rogers and Keshav Pingali. Compiling for Distributed Memory Machines. IEEE Transactions on Parallel and Distributed Systems, 5(3), March 1994.   Keshav Pingali and Kattamuri Ekanadham. Accumulators: New Logic Variable Abstractions for Functional Languages. In Theoretical Computer Science, volume 81, 1991. Available as Cornell CS TR91-1231.   Arvind, Rishiyur Nikhil, and Keshav Pingali. I-structures: Data Structures for Parallel Computing. ACM Transactions on Programming Languages and Systems, 11(4), October 1989. Available as Cornell CS TR87-810.   Keshav Pingali and Kattamuri Ekanadham. Accumulators: New Logic Variable Abstractions for Functional Languages. Theoretical Computer Science, 81, 1991. Available as Cornell CS TR91-1231.   Anne Rogers. Compiling for Locality of Reference. PhD thesis, Cornell University, 1991.   Anne Rogers and Keshav Pingali. Process Decomposition Through Locality of Reference. In Programming Language Design and Implementation, June 1989.   Keshav Pingali and Anne Rogers. Compiler Parallelization of SIMPLE for a Distributed Memory Machine. In International Conference on Parallel Processing, August 1989.   Keshav Pingali. Lazy Evaluation and the Logic Variable. Addison-Wesley, 1987. Available as Cornell CS TR88-952.