Parallel Computers : HW 2
Due: Thusday, Oct 6 by 11:59 pm.
Introduction
For this assignment, you will complete missing pieces of two codes for solving a 1D Poisson problem using Jacobi iteration, and then you will do some basic timing of these codes. The purpose of this homework is not to understand Jacobi iteration as a numerical method, but to ensure that
- You understand how to write basic OpenMP and MPI codes,
- You understand how to run these codes on
crocus, and - You understand the performance modeling ideas we have discussed.
You should do this assignment on your own, though you may ask me for
help, and you can ask anyone high-level questions related to this
homework. When you have completed the homework, you should submit three
files on CMS:
jacobi1d_mpi.c, jacobi1d_omp.c, and a brief
write-up describing the results of the performance experiments outlined
below.
Reference implementation
You should download hw2.tgz to the cluster using
wget http://www.cs.cornell.edu/~bindel/class/cs5220-f11/code/hw2.tgz
Included in this tarball are
jacobi1d.c: a reference serial implementationjacobi1d_omp.c: a partial implementation using OpenMPjacobi1d_mpi.c: a partial implementation using MPIrun_serial.qsub: a queue submission script to run the serial coderun_omp.qsub: a queue script to run the OpenMP code (on 2 cores)run_mpi.qsub: a queue script to run the MPI code (on 2 cores)timing.candtiming.h: some timing routinesMakefile: aMakefilewith rules for building all the codes
The basic syntax of the serial executable jacobi1d.x
is
jacobi1d.x [ncells] [nsteps] [fname]
The ncells and nsteps arguments define the
number of cells in the Poisson discretization and the number of cells in
the Jacobi iteration, respectively. The argument fname is
the name of a file to which the final solution vector is written. Each
row in this file consists of the coordinate for a point in the
discretization and the corresponding solution value; for example, after
1000 steps on a 100000-cell discretization, we have
0 0
1e-05 5e-13
2e-05 1e-12
3e-05 1.5e-12
4e-05 2e-12
...
If ncells or nsteps are omitted, the default
value of 100 is used. If the file name fname is omitted, the
program simply prints out the timings, and does not save the
solution.
Implementation tasks
In jacobi1d_omp.c, your task is to parallelize the
for loops in the function jacobi using OpenMP.
You should do this by copying over the corresponding code from
jacobi.c and putting OpenMP #pragmas in
appropriate places. You should start by putting a #pragma parallel
... outside the outer loop in order to start a parallel section,
and then parallelize the inner loops with #pragma for
directives. I recommend adding a schedule(static) clause to
the latter directives.
The structure of jacobi1d_mpi.c is somewhat more
complicated. In this code, no processor holds the entire solution vector;
instead, each processor has a local piece of the vector, and these pieces
overlap slightly at the ends. No variable is directly updated by more
than one processor; the overlap is simply to accomodate ghost
cells. As a concrete example, suppose we discretize the interval
[0,1] into 10 cells of size 0.1. Then there are 11 points in our mesh,
including the end points subject to boundary conditions. If we partition
these points among three processors, we have the following picture:
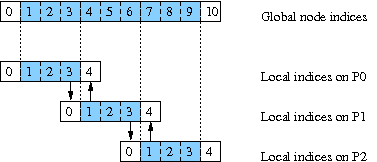
In this picture, the active variables are colored light blue; the white boxes at the end correspond to storage for ghost cells or boundary data. For example, consider the storage on the second processor (P1). Entries 1, 2, and 3 in this processor's local vector correspond to entries 4, 5, and 6 in the global indexing of variables. However, in order to update these entries, P1 must know about the entries 3 and 7 in the global vector. P1 has storage for these variables in position 0 and 4 of its local vector; but rather than computing these variables, P1 must be sent the information from the neighboring processor. Thus, at each step,
- P0 sends entry 3 of its local vector to P1 and receives entry 4;
- P1 sends entry 1 of its local vector to P0 and receives entry 0;
- P1 sends entry 3 of its local vector to P2 and receives entry 4;
- P2 sends entry 1 of its local vector to P1 and receives entry 0
In jacobi1d_mpi.c, I have left out the code that
implements this exchange of ghost cell information. You should fill this
code in. Your code should be correct for any number of processors, not
just two or three. My solution uses MPI_Sendrecv,
MPI_Send, and MPI_Recv in two phases: one that
sends data to the processor to the left, and one that sends data to the
processor to the right. However, if you would prefer to use a different
organization, you are welcome to do so.
For both the OpenMP and the MPI codes, you should check the correctness of your implementation by comparing the solution output files to the solution output files from the serial code.
Running the codes
As in the matrix multiply assignment, you will need to run timing
experiments on the worker nodes by submitting jobs to the batch queueing
system. You can submit a job by preparing a shell script with a few
specially formatted comments that tell the queue management what to do.
For example, the script run_omp.qsub included in the tarball
looks like this:
#!/bin/bash
#
#$ -cwd
#$ -j y
#$ -S /bin/bash
#
N=100000
NSTEPS=1000
export OMP_NUM_THREADS=2
./jacobi1d_omp.x $N $NSTEPS u_omp.out > timing_omp.out
exit 0
The lines beginning with dollar signs respectively say that we want
the worker nodes to start in the same current working directory where we
launched the script; that we want the standard error and standard output
channels to go to the same output file; and that we want to use the bash
shell. After these initial comments, we have the lines that actually run
the program. Note that the OMP_NUM_THREADS environment
variable overrides the default number of threads used by OpenMP (which
would be 8 for the 8-core processors on our cluster) so that we can try
experiments with just two processors. To submit this script to the
queueing system, we could either type make run_omp or
qsub run_omp.qsub.
The default batch script for the MPI code is
run_mpi.qsub:
#!/bin/bash
#
#$ -cwd
#$ -j y
#$ -S /bin/bash
#
N=100000
NSTEPS=1000
MPIRUN=/opt/openmpi/bin/mpirun
$MPIRUN -np $NSLOTS ./jacobi1d_mpi.x $N $NSTEPS u_mpi.out > timing_mpi.out
exit 0
The NSLOTS variable, which gives the number of processors
that are available in the MPI environment, is defined by the queueing
system. For example, to run an MPI job on two cores, we would write
qsub -pe orte 2 run_mpi.qsub
The -pe orte 2 says that we're using an appropriate
parallel environment with two processors. To run on more processors,
change the 2.
Timing experiments
For both the MPI and the OpenMP code, you should do two experiments:
-
Run your codes on two processors with
ncellsequal to 10k, for k = 2, 3, 4, 5, and 6. Plot the ratio of your parallel run times to the serial code run time as a function of k. -
Run your codes with
ncellsof 100,000 on 2-8 processors and produce a speedup plot.
You may produce your plots using gnuplot, TeX, MATLAB, Excel, or whatever else you want.
In addition to running the experiments, you should try to explain your results in terms of a simple performance model that takes into account the time spent on both computation (which is proportional to the number of points per processor) and communication. If you would like, you may use the alpha-beta model parameters described in lecture; or you may fit the communication parameters for yourself. It is okay if your model does not exactly fit the data, but you should at least have the right general behavior. I recommend that you graphically compare your model to the measured timings by putting the model predictions on your plots.