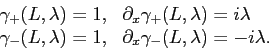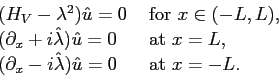Resonance computations and absorbing boundaries

In this section we discuss other methods for computing resonances. They are essential for effective codes for higher dimensional problems for which analogues of (30) are anavailable or become more complicated.

Often, resonances are computed by changing the equation so that it is no longer posed on all of $\mathbb{R}$ , but instead is posed on some interval with homogeneous Dirichlet or Neumann boundary conditions. For example, if the support of lies strictly within the interval , we might add a complex absorbing potential outside of , or we might scale the coordinate system into the complex plane by the method of perfectly matched layers². The change to the equation should be designed so that the modified equation mimics the behavior of the original problem in the range .

To be more concrete, suppose that we modify the equation on the interval so that we still have a nonsingular, second-order, ordinary differential equation in whose coefficients depend on $\lambda$ . Now we specify two linearly independent solutions $\gamma_+(x,\lambda)$ and $\gamma_-(x,\lambda)$ on which satisfy the modified domain equation together with the initial conditions

$\begin{displaymath}\begin{array}{l} \gamma_+(L,\lambda) = 1, \partial_x \gam... ..., \partial_x \gamma_-(L, \lambda) = -i \lambda. \end{array}\end{displaymath}$

(32)

These initial conditions are consistent with the conditions for outgoing and incoming waves on $(L-\epsilon, L)$ . Now suppose that $\gamma(x, \lambda)$ satisfies the differential equation on

, and also the boundary condition $\gamma(M,\lambda) = 0$ . Then

$\displaystyle \gamma(x,\lambda) = c \left( \gamma_+(x, \lambda) + \rho \gamma_-(x, \lambda) \right)$

(33)

where

is an arbitrary constant and

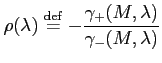
$\displaystyle \rho(\lambda) \stackrel{\rm {def}}{=} -\frac{\gamma_+(M, \lambda)} {\gamma_-(M, \lambda)}$

is a constant whose amplitude reflects how well the equation on

serves to absorb outgoing waves. We can therefore convert the condition at

to a condition at

. Subsituting (32) into (33), we have

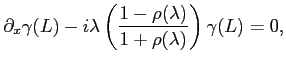
$\displaystyle \partial_x \gamma(L) - i \lambda \left( \frac{1-\rho(\lambda)}{1+\rho(\lambda)} \right) \gamma(L) = 0,$

which, for regions of the complex plane where $\vert\rho(\lambda)\vert$ is small, can be treated as a perturbation of the exact outgoing wave condition at

In summary, by changing the Schrödinger equation outside the interval , imposing homogeneous Dirichlet boundary conditions at $\pm M$ , and then transporting the conditions at $\pm M$ to conditions at $\pm L$ , we arrive at the equations

$\begin{displaymath}\begin{array}{ll} (H_V - \lambda^2) \hat{u} = 0 & \mbox{ for ... ... i \hat{\lambda}) \hat{u} = 0 & \mbox{ at } x = -L. \end{array}\end{displaymath}$

(34)

where

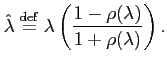
$\displaystyle \hat{\lambda} \stackrel{\rm {def}}{=} \lambda \left( \frac{1-\rho(\lambda)}{1+\rho(\lambda)} \right).$

For values of $\lambda$ where $\vert\rho(\lambda)\vert \ll 1$ , (30) and (34) may be treated each as a perturbation of the other.

The relation between outgoing wave boundary conditions and wave behavior at the boundary of a bounded absorber is useful for applications and experiments as well as for calculations. Experiments to observe acoustic (or electromagnetic) resonances and scattering are generally conducted in anechoic chambers, which are lined with baffles of sound-absorbing material. These baffles prevent incoming reflected waves from interfering with the experiment. Just as one can mimic the ``radiation-only'' property of an infinite domain with a finite absorber, models set in infinite domains are often approximations of models over a large finite domain in which the medium through which waves propogate is slightly dissipative.

David Bindel 2006-10-04