|
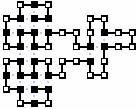
A pruned search tree for
approximating a solution of the 2-dimensional HP model for
protein folding By Department of Computer Science, http://www.cs.cornell.edu/~bensimho Introduction: With completion of the Human Genome Project abundant information from the human DNA sequence has gathered. This information is of limited value when we don’t know the biological meaning of the proteins it encodes for. The 3 dimensional structure of a protein gives us a better idea of its function. The DNA sequence only expresses the linear order of the amino acids of the protein and although it contains all the functional information we are yet unable to determine its function solely from its sequence. Revealing the 3 dimensional structure of a protein experimentally is an expensive and time-consuming procedure and therefore not implemented on all known proteins. Scientists are working on different methods to predict 3 dimensional structures of proteins based on amino acid sequence. Such methods will suggest a 3 dimensional model for a protein with a known linear sequence. These methods will accelerate our understanding of human hereditary information and will enable treatment of genetic diseases and disabilities. Another important aspect of greater economical importance is opening an opportunity for exact (precise) medicine engineering. When a need for a cure to a certain phenomena arises, by defining the 3 dimensional structure of the desired artificial protein needed for the treatment of the problem, use of such methods will provide the amino acid sequence needed to produce the medicine. Description of the problem: The only methods to date that produce reasonable 3D structure predictions are based on resemblance with proteins of known structure (i.e. that were discovered using those sophisticated and expensive procedures). By comparing and aligning linear sequences one can find homologies between such. Statistical investigations have shown that high similarity (above 25%) in sequence implies high probability of functional and structural resemblance. These methods rely on evolutionary connections between the new and the known protein. Usage of such homologies with proteins of known structure will probably enable prediction of about 30% of all proteins. The rest of the proteins fold into structures with no resemblance to ones whose structure has experimentally been reviled. Making predictions on proteins with no homologues of known structure is a real challenge. One approach for prediction based solely on sequence is a search for minimal energy folds within the possible conformations space of a given sequence. Such a search is very complicated since this conformation space is very large. There is a need to confine the search space so that this problem is solvable. One simplification of the problem is to consider only one attribute of the amino acids of the sequence – the polarity of the side chain. Hydrophobic amino acids tend to interact with each other while polar amino acids tend to be on the surface of the protein and interact with the solution. Another simplification is to treat the search space as a lattice – confining consecutive amino acids to adjacent nodes on the lattice. A greater simplification of that is ‘flattening’ the search on a 2 dimensional lattice. This simplification is addressed as HP model. In the HP model, proteins are modeled as sequences of hydrophobic (h) and polar (p) amino acids. The monomers occupy a string of adjacent sites on a 2D lattice. Two h amino acids that are adjacent in space, but not adjacent in sequence, are attracted by a contact energy. All other types of interactions are assumed to be zero. Therefore, the globally optimal conformations in this model are simply those with the maximum possible number of h-h contacts. Although the great loss of information, these simplified models generate behaviors very much like real proteins such as creation of secondary structure motifs. The interactions on the lattice have geometrical resemblance to those of real proteins. So with such modifications one can start predicting 3D structure of proteins even when no homologue of known structure exists. Even with all these simplifications it was shown that the total number of conformations grows exponentially with the length of the sequence, about 2.63n, where n is the length of the sequence. There were many attempts to address this simplified problem. J. Unger and J. Moult compare two methods: Genetic Algorithm (GA) and Monte-Carlo (MC), showing the GA is much better. L. Toma and S. Toma offer a modified MC algorithm called Contact Interactions (CI), and T. Beutler and K. Dill offer their Core-directed chain Growth (CG) algorithm. I will compare my results with theirs. Methods: While most other methods involve ‘jumps’ between various conformations in the conformation space my algorithm attempts to address the problem systematically. It will go over the conformation space via a search tree: place one amino on the lattice and then recursively place the next amino acid in the sequence on all adjacent non-occupied nodes in order. Since this space is of exponential size there is of course a need to prune this search tree. As the algorithm places the amino acids on the lattice it calculates the amount of h-h interactions of the proposed conformation. Since the search tree searches in order, there is no need to calculate all the interactions as a conformation is fully set, but only the difference between it and the last conformation. Actually an easy way to compute number of h-h interactions is adding them as they appear. When each new hydrophobic amino acid is put on the lattice, the number of new interactions it made is added to the total number of interactions. This way calculation of interactions is not redundant. When a hydrophobic amino acid is put on the lattice it has a potential to interact with at most 3 other amino acids. If this amino acid is not the first or last in the sequence it has a potential of making only 2 such interactions. Putting a hydrophobic amino acid between 2 other hydrophobic amino acids occurs only when reaching the end of the sequence since such cases appear on ‘dead ends’. So for most hydrophobic amino acids, when put on the lattice they generate only one h-h interaction. This raises the idea that the h-h interactions potential of a branch of the search tree can be calculated as the conformations are built. A score will be the sum of h-h contacts in the partial conformation + the potential of contacts of all hydrophobic amino acids not yet put on the lattice. This score is an upper limit on the h-h contacts any conformation including ‘sub-conformation’ and a score of a full conformation equals its h-h contacts. If a conformation of x h-h contacts is known, a branch that shows a lower score than x will be pruned, reducing the search space and accelerating the search. The highest score of all conformations achieved up to a certain iteration of the algorithm will be called the goal. For effective pruning there is a need to find a conformation yielding high h-h contacts right on the beginning of the search (i.e. to start with a high goal), or else low potentials won’t be pruned. As a boundary case take an algorithm that starts with a linear conformation. Such a conformation is bound to give 0 contacts and hence worthless, and the score of any branch is always equal or higher. The algorithm uses a heuristic that a high scoring conformation will be dense. The first heuristic used was placing the amino acids in a spiral. Such starting conformation assures compactness in space and proves to be quite successful in yielding high starting scores. The problem with such a starting conformation strategy is its compactness as well. Stages in the work: The first version of the algorithm was as follows. The search tree started with a spiral using a simple 4 state recursion. The potential calculation scheme was as follows: · if the last amino acid in the sequence is a h 3-contact-potential-acids gets a value of 1. · 2-contact-potential-acids are counted as follows:
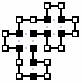
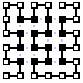
· all hydrophobic amino acid not yet placed are counted as 1-contact-potential-nodes. The sum of these 3 produces a proper potential (amino acids of 3 contacts potential are counted 3 times (under all 3 categories) and amino acids of 2 contacts potential are counted twice). This scheme of potential computation was quite good. Restricted enough to produce high search pruning yet prove to be complete. An algorithm using a heuristic in which the score is always greater or equal to the optimal solution and equalizes on the optimal solution (an ‘admissible scoring function’) is an A-star algorithm and is optimal. So the results of this algorithm are the global maximum of contacts for a sequence. This algorithm worked wonders on shorter sequences (up to 25 amino acids in length). Longer sequences needed greater pruning. A new, non-optimal (non admissible) scoring scheme was put to work. Now each hydrophobic amino acid not on yet board has a potential of one + epsilon, except for the last few who had a potential of 2 + epsilon. ‘Few’ and ‘epsilon’ were actually parameters to play with, practically, for running time purposes, chosen to be 6 and 0.1 respectively. This heuristic has proved to be much faster and yielded optimal results in most cases checked. The dense spiral starting conformation has a fault. It is ‘trapped’ by itself and is not dynamic. Another heuristic for starting conformation implemented is the ‘snake shape’ (see table). This not only yields relatively high scores in early running stages of the algorithm, but is also very dynamic and ‘open’. Table 1: 'snake shape' and 'spiral shape' starting conformations
Table 2: stages in the algorithm using different starting conformations
Since the starting condition is so crucial here, both for a high starting score and because of the heuristics non-optimality it proved very helpful to search each string twice – reading it both from right to left and from left to right. This is also the final algorithm in use. Results: A comparison of the results of other methods with this new algorithm on 8 sequences from the literature was done: Table 3: sequences from the literature used for comparison of methods[1]
Table 4: comparison of other methods with the new one[2],[3]
max – maximum contacts of best conformation reached. time – cpu time in seconds, where known. So though this algorithm is an extensive search, and is likely to grow exponentially with the length of the sequence, it is still of reasonable running time compared with other existing methods. In most cases it reaches the global maximum in a relatively short time. A major drawback of the algorithm is its non-optimality – on the 9th sequence it reaches a comparably low score. Another drawback is its running time varies greatly on different sequences of the same length. It is hard to estimate how long will it take the algorithm to complete the search (the option of limiting the search time was implemented for this reason, and partial results are available midst running). The algorithm
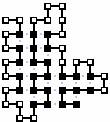
discovered that the 60-mer (sequence #8) others believed were the global
minima are, in fact, only local minima. While others reached a limit of 35
contacts this algorithm produced a 36 contact conformation (The conformation
found for this 60-mer is given as #8 sequence below).
The best conformations to all 8 sequences is given here:
Conclusions:
This new algorithmic approach proposed is not guaranteed to produce an optimal conformation, but can give meaningful results in a relatively short time. It has also proved to find one conformation that all other methods could not find. There are still some improvements that can be implemented on this algorithm such as: · Starting the recursion from the middle point of the sequence and advancing in a bi-directional manner. · Optimizing the parameters of the heuristic function. The 3 dimensional HP problem is more interesting than the 2 dimensional one. Moving from a 2 dimensions to 3 dimensions with this algorithm needs some thinking. Choosing a recursion to cover the conformation space. Choosing a good ‘starting conformation’. Deciding on potential estimation functions and a scoring scheme. This is kept for another project. You are invited to visit the project’s website at: http://www.cs.cornell.edu/~bensimho/lattice This research was supported by
a grant from the Ministry of Science, Dates of conduct: October 2000 to October 2001. Supervisors: Prof. Daniel Berend, Dr. Daniel Fischer, Acknowledgements: Dani Levit, Nir Esterman, Amir Mishaeli & Yael Mandelblat, who all in a way challenged me think, chipped in with new ideas, helped me find literature, and who in general encouraged me through this whole process. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||