Jon Kleinberg 2
But existing models are insufficient to explain the striking algorithmic component of Milgram's original findings: that individuals using local information are collectively very effective at actually constructing short paths between two points in a social network. Although recently proposed network models are rich in short paths, we prove that no decentralized algorithm, operating with local information only, can construct short paths in these networks with non-negligible probability. We then define an infinite family of network models that naturally generalizes the Watts-Strogatz model, and show that for one of these models, there is a decentralized algorithm capable of finding short paths with high probability. More generally, we provide a strong characterization of this family of network models, showing that there is in fact a unique model within the family for which decentralized algorithms are effective.
Milgram's basic small-world experiment remains one of the most compelling ways to think about the problem. The goal of the experiment was to find short chains of acquaintances linking pairs of people in the United States who did not know one another. In a typical instance of the experiment, a source person in Nebraska would be given a letter to deliver to a target person in Massachusetts. The source would initially be told basic information about the target, including his address and occupation; the source would then be instructed to send the letter to someone she knew on a first-name basis in an effort to transmit the letter to the target as efficaciously as possible. Anyone subsequently receiving the letter would be given the same instructions, and the chain of communication would continue until the target was reached. Over many trials, the average number of intermediate steps in a successful chain was found to lie between five and six, a quantity that has since entered popular culture as the ``six degrees of separation'' principle [7].
(Most of the early work on this issue, beginning with analysis of Pool and Kochen that pre-dated Milgram's experiments [16], was based on versions of the following explanation: random networks have low diameter. (See for example the book of surveys edited by Kochen [11].) That is, if every individual in the United States were to have a small number of acquaintances selected uniformly at random from the population -- and if acquaintanceship were symmetric -- then two random individuals would be linked by a short chain with high probability. Even this early work recognized the limitations of a uniform random model; if A and B are two individuals with a common friend, it is much more likely that they themselves are friends. But at the same time, a network of acquaintanceships that is too ``clustered'' will not have the low diameter that Milgram's experiments indicated.) Why should there exist short chains of acquaintances linking together arbitrary pairs of strangers?
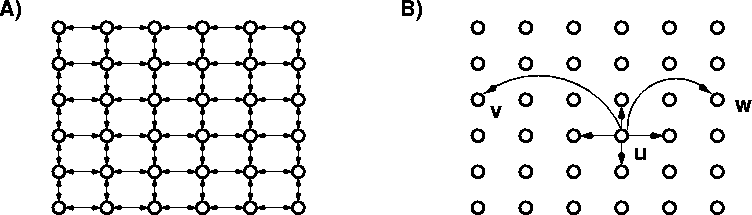
Recently, Watts and Strogatz proposed a model for the small-world phenomenon based on a class of random networks that interpolates between these two extremes, in which the edges of the network are divided into ``local'' and ``long-range'' contacts [19]. The paradigmatic example they studied was a ``re-wired ring lattice,'' constructed roughly as follows. One starts with a set V of n points spaced uniformly on a circle, and joins each point by an edge to each of its k nearest neighbors, for a small constant k. These are the ``local contacts'' in the network. One then introduces a small number of edges in which the endpoints are chosen uniformly at random from V -- the ``long-range contacts''. Watts and Strogatz argued that such a model captures two crucial parameters of social networks: there is a simple underlying structure that explains the presence of most edges, but a few edges are produced by a random process that does not respect this structure. Their networks thus have low diameter (like uniform random networks), but also have the property that many of the neighbors of a node uare themselves neighbors (unlike uniform random networks). They showed that a number of naturally arising networks exhibit this pair of properties (including the connections among neurons in the nematode species C. elegans, and the power grid of the Western U.S.); and their approach has been applied to the analysis of the hyperlink graph of the World Wide Web as well [1].
Networks that are formed from a superposition of a ``structured subgraph'' and a ``random subgraph'' have been investigated in the area of probabilistic combinatorics. In a fundamental instance of such an approach, Bollobás and Chung [5] gave bounds on the diameter of the random graph obtained by adding a random matching to the nodes of a cycle. (See also [6].)
(It is important to note that Question () Why should arbitrary pairs of strangers be able to find short chains of acquaintances that link them together?
In this work, we study ``decentralized'' algorithms by which individuals, knowing only the locations of their direct acquaintances, attempt to transmit a message from a source to a target along a short path. Our central findings are the following.
 |
In designing our network model, we seek a
simple framework that encapsulates the paradigm of
Watts and Strogatz -- rich in local connections,
with a few long-range connections.
Rather than using a ring as the basic structure, however,
we begin from a two-dimensional grid and allow for
edges to be directed.
Thus, we begin with a set of nodes (representing
individuals in the social network) that are identified
with the set of lattice points in an
![]() square,
square,
![]() and we define the lattice distance between two
nodes (i,j) and
and we define the lattice distance between two
nodes (i,j) and ![]() to be the number of
``lattice steps'' separating them:
to be the number of
``lattice steps'' separating them:
![]() For a universal constant
For a universal constant ![]() ,
the node u has a directed edge
to every other node within
lattice distance p -- these are its local contacts.
For universal constants
,
the node u has a directed edge
to every other node within
lattice distance p -- these are its local contacts.
For universal constants ![]() and
and ![]() ,
we also construct directed edges from u to qother nodes (the long-range contacts) using independent random trials;
the
,
we also construct directed edges from u to qother nodes (the long-range contacts) using independent random trials;
the
![]() directed edge from u has endpoint vwith probability proportional to
[d(u,v)]-r.
(To obtain a probability distribution, we divide this quantity by
the appropriate normalizing constant
directed edge from u has endpoint vwith probability proportional to
[d(u,v)]-r.
(To obtain a probability distribution, we divide this quantity by
the appropriate normalizing constant
![]() ;
we will call this the inverse
;
we will call this the inverse
![]() -power distribution.)
-power distribution.)
This model has a simple ``geographic'' interpretation: individuals live on a grid and know their neighbors for some number of steps in all directions; they also have some number of acquaintances distributed more broadly across the grid. Viewing p and q as fixed constants, we obtain a one-parameter family of network models by tuning the value of the exponent r. When r = 0, we have the uniform distribution over long-range contacts, the distribution used in the basic network model of Watts and Strogatz -- one's long-range contacts are chosen independently of their position on the grid. As r increases, the long-range contacts of a node become more and more clustered in its vicinity on the grid. Thus, r serves as a basic structural parameter measuring how widely ``networked'' the underlying society of nodes is.
The algorithmic component of the model is based on Milgram's experiment. We start with two arbitrary nodes in the network, denoted s and t; the goal is to transmit a message from s to tin as few steps as possible. We study decentralized algorithms, mechanisms whereby the message is passed sequentially from a current message holder to one of its (local or long-range) contacts, using only local information. In particular, the message holder u in a given step has knowledge of
The reader may worry that assumption (iii) above gives a decentralized algorithm too much power. However, it only strengthens our results: our lower bounds will hold even for algorithms that are given this knowledge, while our upper bounds make use of decentralized algorithms that only require assumptions (i) and (ii).
When r = 0 -- the uniform distribution over long-range contacts --
standard results from random graph theory can be used to show
that with high probability there exist paths
between every pair of nodes
whose lengths are bounded by a polynomial in ![]() ,
exponentially
smaller than the total number of nodes.
However, there is no way for a
decentralized algorithm to find these chains:
,
exponentially
smaller than the total number of nodes.
However, there is no way for a
decentralized algorithm to find these chains:
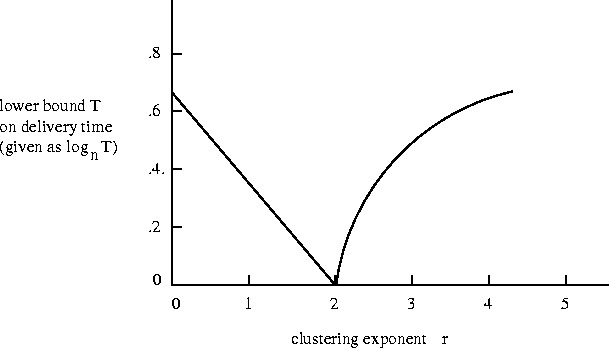
As the parameter r increases, a decentralized algorithm can take more advantage of the ``geographic structure'' implicit in the long-range contacts; at the same time, long-range contacts become less useful in moving the message a large distance. There is a value of r where this trade-off can be best exploited algorithmically; this is r = 2, the inverse-square distribution.
This pair of theorems reflects a fundamental consequence of our model. When long-range contacts are formed independently of the geometry of the grid, short chains will exist but the nodes, operating at a local level, will not be able to find them. When long-range contacts are formed by a process that is related to the geometry of the grid in a specific way, however, then short chains will still form and nodes operating with local knowledge will be able to construct them.
We now comment on the ideas underlying the proofs of these results;
the full details are given in the subsequent sections.
The decentralized algorithm ![]() that achieves the bound
of Theorem 2 is the following simple rule:
in each step, the current message-holder uchooses a contact that is as close to the target t as possible,
in the sense of lattice distance.
Note that algorithm
that achieves the bound
of Theorem 2 is the following simple rule:
in each step, the current message-holder uchooses a contact that is as close to the target t as possible,
in the sense of lattice distance.
Note that algorithm ![]() makes use of even less information
than is allowed by our general model: the current message
holder does not need to know anything about the set of
previous message holders.
To analyze an execution of algorithm
makes use of even less information
than is allowed by our general model: the current message
holder does not need to know anything about the set of
previous message holders.
To analyze an execution of algorithm ![]() ,
we say
that it is in phase j if the lattice distance
from the current message holder to the target is between
2j and 2j+1.
We show that in phase j,
the expected time before the current message holder has
a long-range contact within lattice distance
2j of t is bounded proportionally to
,
we say
that it is in phase j if the lattice distance
from the current message holder to the target is between
2j and 2j+1.
We show that in phase j,
the expected time before the current message holder has
a long-range contact within lattice distance
2j of t is bounded proportionally to ![]() ;
at this point, phase j will come to an end.
As there are at most
;
at this point, phase j will come to an end.
As there are at most
![]() phases,
a bound proportional to
phases,
a bound proportional to
![]() follows.
Interestingly, the analysis matches our intuition,
and Milgram's description,
of how a short chain is found in real life:
``The geographic movement of the [message] from
Nebraska to Massachusetts is striking.
There is a progressive closing in on the target area
as each new person is added to the chain'' [13].
follows.
Interestingly, the analysis matches our intuition,
and Milgram's description,
of how a short chain is found in real life:
``The geographic movement of the [message] from
Nebraska to Massachusetts is striking.
There is a progressive closing in on the target area
as each new person is added to the chain'' [13].
The impossibility result of Theorem 1 is based, fundamentally, on the fact that the uniform distribution prevents a decentralized algorithm from using any ``clues'' provided by the geometry of the grid. Roughly, we consider the set U of all nodes within lattice distance n2/3 of t. With high probability, the source s will lie outside of U, and if the message is never passed from a node to a long-range contact in U, the number of steps needed to reach t will be at least proportional to n2/3. But the probability that any message holder has a long-range contact in U is roughly n-2/3, so the expected number of steps before a long-range contact in U is found is at least proportional to n2/3 as well.
 |
More generally, we can show a strong characterization
theorem for this family of models:
r = 2 is the only
value for which there is a decentralized algorithm
capable of producing chains whose length is a
polynomial in ![]() :
:
(b) Let r > 2.
There is a constant ![]() ,
depending on p, q, r,
but independent of n,
so that the expected delivery time
of any decentralized algorithm is at least
,
depending on p, q, r,
but independent of n,
so that the expected delivery time
of any decentralized algorithm is at least
![]()
The complete proof of this theorem is given in Section 3. The proof of (a) is analogous to that of Theorem 1. The proof of (b), on the other hand, exposes a ``dual'' obstacle for decentralized algorithms: with a large value of r, it takes a significant amount of time before the message reaches a node with a long-range contact that is far away in lattice distance. This effectively limits the ``speed'' at which the message can travel from s to t.
Although we have focused on the two-dimensional grid,
our analysis can be applied more broadly.
We can generalize our results to k-dimensional
lattice networks, for constant values of k,
as well as less structured graphs with analogous scaling properties.
In the k-dimensional case, a decentralized
algorithm can construct paths of length
polynomial in ![]() if and only if r = k.
if and only if r = k.
The results suggest a fundamental network property, distinct from diameter, that helps to explain the success of small-world experiments. One could think of it as the ``transmission rate'' of a class of networks: the minimum expected delivery time of any decentralized algorithm operating in a random network drawn from this class. Thus we see that minimizing the transmission rate of a network is not necessarily the same as minimizing its diameter. This may seem counter-intuitive at first, but in fact it formalizes a notion raised initially -- in addition to having short paths, a network should contain latent structural cues that can be used to guide a message towards a target. The dependence of long-range connections on the geometry of the lattice is providing precisely such implicit information.
Indeed, the proofs of the theorems reveal a general
structural property that implies the optimality of the exponent r = 2for the two-dimensional lattice:
it is the unique exponent at which a node's long-range
contacts are nearly uniformly distributed over all ``distance scales.''
Specifically, given any node u, we can partition the remaining
nodes of the lattice into sets
![]() ,
where Aj consists of all nodes whose lattice distance
to u is between 2j and 2j+1.
These sets naturally correspond to different levels of ``resolution''
as we move away from u; all nodes in each Aj are at
approximately the same distance (to within a factor of 2) from u.
At exponent r = 2, each long-range contact of u
is nearly equally likely to belong to any of the sets Aj;
when r < 2, there is a bias toward sets Aj at greater distances,
and when r > 2, there is a bias toward sets Aj at nearer distances.
,
where Aj consists of all nodes whose lattice distance
to u is between 2j and 2j+1.
These sets naturally correspond to different levels of ``resolution''
as we move away from u; all nodes in each Aj are at
approximately the same distance (to within a factor of 2) from u.
At exponent r = 2, each long-range contact of u
is nearly equally likely to belong to any of the sets Aj;
when r < 2, there is a bias toward sets Aj at greater distances,
and when r > 2, there is a bias toward sets Aj at nearer distances.
We now present proofs of the theorems discussed in the previous section. When we analyze a decentralized algorithm, we can adopt the following equivalent formulation of the model, which will make the exposition easier. Although our model considers all long-range contacts as being generated initially, at random, we invoke the ``Principle of Deferred Decisions'' -- a common mechanism for analyzing randomized algorithms [14] -- and assume that the long-range contacts of a node v are generated only when the message first reaches v. Since a decentralized algorithm does not learn the long-range contacts of v until the message reaches v, this formulation is equivalent for the purposes of analysis.
A comment on the notation: ![]() denotes the logarithm base 2,
while
denotes the logarithm base 2,
while ![]() denotes the natural logarithm, base e.
denotes the natural logarithm, base e.
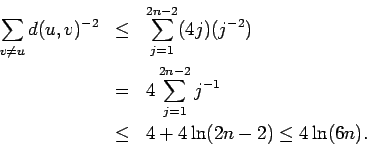
The decentralized algorithm ![]() is defined as follows:
in each step, the current message-holder uchooses a contact that is as close to the target t as possible,
in the sense of lattice distance.
For j > 0,
we say that the execution of
is defined as follows:
in each step, the current message-holder uchooses a contact that is as close to the target t as possible,
in the sense of lattice distance.
For j > 0,
we say that the execution of ![]() is in phase j when
the lattice distance from the current node to t is
greater than 2j and at most 2j+1.
We say
is in phase j when
the lattice distance from the current node to t is
greater than 2j and at most 2j+1.
We say ![]() is in phase 0 when the lattice distance to t is at most 2.
Thus, the initial value of j is at most
is in phase 0 when the lattice distance to t is at most 2.
Thus, the initial value of j is at most ![]() .
Now, because the distance from the message to the target
decreases strictly in each step, each node that becomes
the message holder has not touched the message before;
thus, we may assume that the long-range contact from
the message holder is generated at this moment.
.
Now, because the distance from the message to the target
decreases strictly in each step, each node that becomes
the message holder has not touched the message before;
thus, we may assume that the long-range contact from
the message holder is generated at this moment.
Suppose we are in phase j,
![]() ,
and the current message holder is u.
What is the probability that phase j will end in this step?
This requires the message to enter the
set Bj of nodes within lattice distance 2j of t.
There are at least
,
and the current message holder is u.
What is the probability that phase j will end in this step?
This requires the message to enter the
set Bj of nodes within lattice distance 2j of t.
There are at least
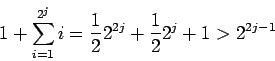
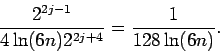
Let Xj denote total number of steps
spent in phase j,
![]() .
We have
.
We have
![\begin{eqnarray*}EX_j & = & \sum_{i=1}^\infty
{\rm Pr}\left[{X_j \geq i}\right]...
...(1 - \frac{1}{128 \ln (6n)}\right)^{i-1} \\
& = & 128 \ln (6n).
\end{eqnarray*}](img37.gif)
Now, if X denotes the total number of steps spent by
the algorithm, we have
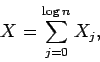
We first expand our model of a decentralized algorithm slightly; it will correspondingly strengthen the result to show a lower bound for this new model. An algorithm initially has knowledge of the grid structure, all the local contacts, and the locations of s and t. In step i, some set Si of nodes has touched the message. At this point, the algorithm has knowledge of all long-range contacts of all nodes in Si. (Following our style of analysis, the long-range contacts of other nodes will be constructed only as the message reaches them.) Based on this information, it chooses any contact v of any node in Si that has not yet received the message -- v need not be a contact of the current message holder -- and it sends the message to v. The set Si+1 thus contains one element more than Si, and the algorithm iterates. This is the same as our initial model of a decentralized algorithm, except that we do not count steps in which the algorithm ``backtracks'' by sending the message through a node that has already received it.
For technical reasons, we will add one additional feature to
the algorithms we consider.
An algorithm will run for an infinite sequence of steps;
initially it behaves as above, and once the message reaches
t, the message remains at t in all subsequent steps.
Thus, when we consider the
![]() step of a given algorithm,
we need not worry that it has already terminated by this step.
step of a given algorithm,
we need not worry that it has already terminated by this step.
We now prove the two parts of Theorem 3; note that part (a) implies Theorem 1 by setting r = 0. As in Section 2, we will invoke the Principle of Deferred Decisions [14] in the analysis.
Note that because we have the freedom to choose
the constant ![]() ,
we may also assume that nis at least as large as some fixed absolute constant n0.
The probability that a node u chooses v as its
,
we may also assume that nis at least as large as some fixed absolute constant n0.
The probability that a node u chooses v as its
![]() out of q long-range contacts is
out of q long-range contacts is
![]() ,
and we have
,
and we have
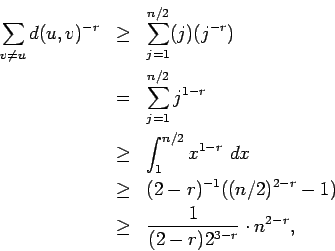
Let U denote the set of nodes within lattice distance
![]() of t.
Note that
of t.
Note that
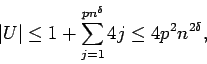
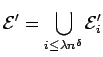 .
Now, the node reached at step i has
q long-range contacts that are generated at random
when it is encountered; so we have
.
Now, the node reached at step i has
q long-range contacts that are generated at random
when it is encountered; so we have
![\begin{eqnarray*}{\rm Pr}\left[{{\cal E}_i'}\right]
& \leq & \frac{q \vert U\ve...
...-r}} \\
& = & \frac{(2-r) 2^{5-r} qp^2 n^{2 \delta}}{n^{2-r}} .
\end{eqnarray*}](img55.gif)
![\begin{eqnarray*}{\rm Pr}\left[{{\cal E}'}\right]
& \leq & \sum_{i \leq \lambda...
...a}}{n^{2-r}} \\
& = & (2-r) 2^{5-r} \lambda q p^2 \leq \frac14.
\end{eqnarray*}](img56.gif)
We now define two further events.
Let ![]() denote the event that the chosen source sand target t are separated by a lattice distance of at least n/4.
One can verify that
denote the event that the chosen source sand target t are separated by a lattice distance of at least n/4.
One can verify that
![]() .
Since
.
Since
![]() ,
,
![]()
Finally, let X denote the random variable equal
to the number of steps taken for the message to reach t,
and let ![]() denote the event that the message
reaches t within
denote the event that the message
reaches t within
![]() steps.
We claim that if
steps.
We claim that if ![]() occurs and
occurs and ![]() does not occur,
then
does not occur,
then ![]() cannot occur.
For suppose it does.
Since
cannot occur.
For suppose it does.
Since
![]() ,
in any s-t path of at most
,
in any s-t path of at most
![]() steps,
the message must be passed at least once from
a node to a long-range contact.
Moreover, the final time this happens, the long-range
contact must lie in U.
This contradicts our assumption that
steps,
the message must be passed at least once from
a node to a long-range contact.
Moreover, the final time this happens, the long-range
contact must lie in U.
This contradicts our assumption that ![]() does not occur.
does not occur.
Thus,
![]() ,
hence
,
hence
![]() .
Since
.
Since
![\begin{displaymath}EX \geq
E\left[{X}~\vert~{{\cal F}\wedge \overline{{\cal E}'...
...\overline{{\cal E}'}}\right]
\geq \frac14 \lambda n^{\delta},\end{displaymath}](img65.gif)
![\begin{eqnarray*}{\rm Pr}\left[{d(u,v) > m}\right]
& \leq & \sum_{j=m+1}^{2n-2}...
...& \leq & (r-2)^{-1} m^{2-r} = \varepsilon^{-1} m^{-\varepsilon}.
\end{eqnarray*}](img67.gif)
We set
![]() ,
,
![]() ,
and
,
and
![]() .
We will assume n has been chosen large enough that
.
We will assume n has been chosen large enough that
![]() .
Let
.
Let
![]() be the event that in step i,
the message reaches a node
be the event that in step i,
the message reaches a node ![]() that has a long-range contact v satisfying
that has a long-range contact v satisfying
![]() .
Let
.
Let
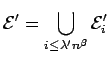 be the event that this happens
in the first
be the event that this happens
in the first
![]() steps.
We have
steps.
We have
![\begin{eqnarray*}{\rm Pr}\left[{{\cal E}'}\right]
& \leq & \sum_{i \leq \lambda...
...silon\gamma} \\
& = & \lambda' q \varepsilon^{-1} \leq \frac14.
\end{eqnarray*}](img76.gif)
As in part (a), we define ![]() to be the event
that s and t are separated by a lattice distance of at least n/4.
Observe that
to be the event
that s and t are separated by a lattice distance of at least n/4.
Observe that
![]() Let X denote the random variable equal
to the number of steps taken for the message to reach t,
and let
Let X denote the random variable equal
to the number of steps taken for the message to reach t,
and let ![]() denote the event that the message
reaches t within
denote the event that the message
reaches t within
![]() steps.
We claim that if
steps.
We claim that if ![]() occurs and
occurs and ![]() does not occur,
then
does not occur,
then ![]() cannot occur.
For if
cannot occur.
For if ![]() does not occur, then the message can move
a lattice distance of at most
does not occur, then the message can move
a lattice distance of at most ![]() in each of its
first
in each of its
first
![]() steps.
This is a total lattice distance of at most
steps.
This is a total lattice distance of at most
Thus
![]() .
Since
.
Since
![\begin{displaymath}EX \geq
E\left[{X}~\vert~{{\cal F}\wedge \overline{{\cal E}'...
... \overline{{\cal E}'}}\right]\geq \frac14 \lambda' n^{\beta},\end{displaymath}](img80.gif)
Algorithmic work in different settings has considered the problem of routing with local information; see for example the problem of designing compact routing tables for communication networks [15] and the problem of robot navigation in an unknown environment [3]. Our results are technically quite different from these; but they share the general goal of identifying qualitative properties of networks that makes routing with local information tractable, and offering a model for reasoning about effective routing schemes in such networks. While we have deliberately focused on a very clean model, we believe that a more general conclusion can be drawn for small-world networks: that the correlation between local structure and long-range connections provides fundamental cues for finding paths through the network. When this correlation is near a critical threshold, the structure of the long-range connections forms a type of ``gradient'' that allows individuals to guide a message efficiently toward a target. As the correlation drops below this critical value and the social network becomes more homogeneous, these cues begin to disappear; in the limit, when long-range connections are generated uniformly at random, our model describes a world in which short chains exist but individuals, faced with a disorienting array of social contacts, are unable to find them.
This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 swn.tex.
![]()