Detecting Byzantine Failures Transparently

Authors: Brandon Bray and Jed Liu

Summary: Fault tolerance is increasingly important to scientific applications, which are demanding longer running times.  The running time of some applications are so long that it is almost certain that a hardware failure will occur.  For the most part, these failures fall into the fail-stop category — that is, a hardware failure results in the cessation of the hardware's functionality.  Since so many of these failures are fail-stop, most of the research has addressed this.  We are interested in another type of failure, the Byzantine failure — a processor that returns incorrect results.  First we work on detecting such failures and running experiments on a modified matrix-multiply routine.  After detecting these failures, we were interested in ways to recover from such failures.  Lastly, our interest is adding this to a compiler, making the whole detection of Byzantine failures transparent to the programmer.

Fail-Stop Failures

In terms of distributed computing, computations aren't necessarily placed in controlled environments such as super-computers.  Often it is the case that someone is trying to take advantage of a sparsely used public lab.  In these cases, a fail-stop failure is entirely possible for a number of reasons, including an actual hardware failure, a network disconnection, or a public computer needs to relinquish time to a local user.  One thing that characterizes fail-stop failures is that they are easy to detect.  Essentially, computational progress stops, which can be detected because of timeouts on network pings or similar diagnostics.

Because fail-stop failures are relatively common, (and even expected), in addition to being easy to detect, much of the work towards addressing these failures is in preparing for the failure and then recovering from them.  A cursory understanding of the various techniques is all that one needs to see how interesting and important this field is.  The more important techniques include check pointing and message logging.  Combining the two have usefulness for rolling back computations to a point where all the processors can continue their work.  This saves the application from the most devastating case where all computation must begin from scratch.  While fail-stop failures are interesting, it isn't the area we set out to explore.  Nevertheless, adapting techniques developed for this specific error seems prudent, hence we looked at the following papers in search of ideas:

  1. Kim, Plank, and Dongarra:  This paper addresses detecting and recovering from fail-stop failures in a number of matrix routines.  The primary idea here is to add a checksum to all the routines.  The checksum is used during the rollback of computation.  The checksum approach introduces concerns about overflow, underflow, and possible cancellation-error.  To be sure, a checksum is not a perfect solution, but it is a practical one.  Most importantly, inserting checksums into these routines only adds a small overhead to the running time.  In the end, we agreed that a checksum is an attractive approach to handling Byzantine failures.  One thing to note is that checksums were not used to detect the failures here, but rather were used to recover from the failures.  Our approach would use the checksums for the primary use of detecting the failure, not recovering from it.
  2. Smith, and Shrivastava:  In this paper, which is mostly a case study, the authors looked at making use of a sparsely used public lab to compute matrix-multiplications.  The approach taken is referred to as "A Bag of Tasks".  Basically, a master computer divides the computation into a number of tasks.  What characterizes these tasks is that they are all independent, meaning that the tasks do not require interaction with each other.  This last requirement is easy to ensure with matrix-multiplication, but is not a characteristic for a majority of parallel computations.  After creating the bag of tasks, workers ask the master for a single task to work on.  A fail-stop failure occurs whenever the result of computing the task does not return, usually determined by a timeout.  This approach is quite similar to that of the SETI@Home, project which distributes work to a number of personal computers.  While there isn't much to take away from this and apply to handling Byzantine failures, this approach to computation could greatly benefit from work on handling Byzantine failures (more explained later).
  3. Gunnels, Katz, Quintana-Ortí, and van de Geijn:  We found this paper to be the closest to what we were interested in doing; however, this paper too does not directly deal with Byzantine failures.  The authors of this paper were concerned about the data for computations being corrupted during the computation.  This could happen in examples such as outer space satellites that suffer from radiation causing bits to flip unexpectedly.  Their approach is to compute checksums for the data before the computation and compare these to checksums computed after the computation.  The checksums are stored in a vector, so there is a separate checksum for each row or column of a matrix.  Using these checksums and the comparisons, it is possible to determine exactly where the corruption occurred.  This clearly is not a fail-stop failure, and closer to a Byzantine failure.  However, the failure is not the processor's.  It is a failure in the storage, which for the most part is extremely rare inside the ionosphere, not to mention error correction codes have almost eliminated this problem.  Indeed, we were interested in finding out whether a processor's computation is incorrect.  What we did find in this paper was a real explanation of the overhead -- roughly twenty-five percent.  Since our approach involved checksums, we felt that this provided a nice point of comparison.

Byzantine Failures

Before setting out on solving problems arising from Byzantine failures, it is important to define exactly what a Byzantine failure is.  For our purposes, we say a processor has a Byzantine failure when the incorrect answer results from a computation.  In a distributed environment, this may not necessarily be due to a processor, but rather the medium of communication.  To be sure, it is not unrealistic to believe that a message sent over a network becomes corrupted in some manner.  Nevertheless, in most situations where the medium of communication is possibly untrustworthy, from networking all the way to main memory, effort has been focused on error correcting codes.  Thus, it is reasonable to assume that any medium of communication will reliably report the result a processor declares as the answer to a computation.  This narrows the scope of Byzantine failures down to the processor itself.  If a processor returns an incorrect result, there isn't any hardware to reassure us that the correct result was computed.  Indeed, whether a processor returns the wrong result because of a bug, or due to a malicious design, we really don't care — an incorrect computation simply is classified as a Byzantine failure.

Now, this begs the question that different architectures were designed with different accuracies in mind.  Some architectures could certainly compute a value with more accuracy than another.  Is the less accurate computation a failure?  Clearly, it would be zealous to think so.  Not only that, but for most computations, applications rarely push the limits of architectural accuracy.  Thus, for practical purposes, we ignore this issue entirely.  Actually, most applications will be distributed over similar architectures, so such an issue will not appear except for an extremely small number of cases.  The third paper mentioned above takes this into account by introducing a tolerance value so that rounding issues are avoided.  In our tests, we will use exact equality for measurements, which is no compromise since the work is distributed over computers that all have the exact same architecture.

Lastly, just how often do these failures occur?  To be truthful, not often.  Actually, it was reasonable to assume that they would never happen during our experiments, regardless of the rain dances we did in the lab.  But there is evidence that such failures might be more of an issue in the future.  For starters there are examples pertaining solely to Intel's Pentium processor line:

What is heartening after reading the examples above is that all these sources of failures were discovered relatively early.  Not only that, but the consumer community has zero tolerance for this type of failure.  Using hardware that has been available for a period of time dramatically reduces the exposure to Byzantine failures.  Nevertheless, we state that these risks do exist, and therefore we would like to devise a system that begins to address the problem.

Indeed, one last situation where a Byzantine failure is very likely is one in which the processors doing the computation are not trusted.  One such example is SETI@Home, where computers are volunteered to help with processing data collected from the Arecibo receiver in Puerto Rico.  Many people in their fervor to be at the top of the list have resorted to lying about the results of some computations in order to increase the number of blocks submitted.  This is clearly the case of a malicious worker, where the processor itself has had no part in the crime.  Without verification of the data, valuable data may be lost or ignored.

Our Experiment

The first problem to solve in dealing with Byzantine failures is detecting them.  This is done by verifying the results of a computation by duplicating the work on two or more processors.  If all the processors agree on the results, then it is unlikely that a Byzantine failure occurred.  So, dividing up the number of useful processors for a given application certainly introduces some initial costs: if half as many processors are available to work on one computation, then the work will be done in twice the time.  Our main priority is adding as little overhead to this as possible.  Comparing the entire state of one processor with another is definitely not an option.  The next best alternative is having the two processors compute checksums and then comparing the checksums.  Checksums are not perfect, though, as it is possible for two checksums to match even though the state or result of the computations disagree.  For a high-quality checksum, however, this is very unlikely.  In general, the quality of a checksum is inversely proportional to the risk of a false positive (two checksums agreeing for different data).

Going with the checksum approach, we took a very simple approach to parallel matrix-multiplication and modified it.  We chose a simple matrix-multiply routine over more complicated and efficient ones because we wanted to analyze the results with more accuracy.  We will later discuss how the results extend to more efficient implementations of matrix multiplication.  For now, our matrix multiply routine without any check-summing or preparation for fault-tolerance works as follows.  For A x B = C:

  1. A master processor (the one designated as processor zero) finds out how many processors are available to do work.  The set of all processors but excluding the master processor is referred to as the workers.
  2. The rows of matrix A are equally divided among the workers and sent to each worker processor.
  3. The entire matrix B is sent to each worker processor.
  4. Each worker computes its part of the C matrix, and send the results back to the master processor.
  5. The master processor collects the results from the workers and assembles the C matrix.

In order to account for Byzantine failures, we modify the above steps by doing the following:

  1. The master processor after, finding the number of workers available, divides them into two equal groups, pairing each processor in one group with a processor in the other.
  2. Each pair of worker processors receives the same rows of matrix A.
  3. Every worker processor again receives all of matrix B.
  4. Each worker computes its part of the C matrix and alongside it computes a checksum (which is basically the sum of all the elements that part of the C matrix).  The checksum is sent back to the master.
  5. The master now receives checksums from each pair, which it can compare to determine whether a Byzantine failure has occurred.  After comparing the checksums, the master receives the results from only one of the processors.

The code for the two routines is available here: unchecked and checked.

Now, some concerns arise from this approach which we will address before talking about the results.  First, given that everything is computed on systems that are each exactly alike, wouldn't they all produce the same faulty results?  True, this is a concern.  The best way to avoid this is have a slightly heterogeneous collection of processors.  If each processor is based on a slightly different architecture, but they all hold to the same convention (e.g. little-endian), this issue is mostly eliminated.  In some cases where Byzantine failures occur due to a processor overheating or something similar, a homogenous environment is perfectly suitable.  Second, aren't there better checksums than simply summing up the elements of the respective parts of the C matrix?  Certainly, yet the usefulness of different checksums isn't significant for our purpose which is to detect Byzantine failures.  Other techniques for checksums are considered later in our discussion.

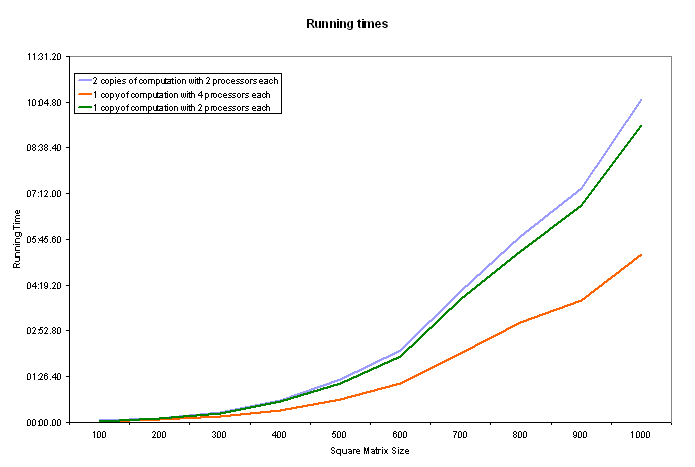
The first question we would like to answer is, how much overhead are we introducing by performing the checksum?  We ran the matrix-multiply routine for square matrices of sizes 100 through 1000.  First, we allowed all the processors to work on the multiplication without any checksums.  Then we ran the same computations on half the processors without checksums.  Lastly, we ran our modified matrix-multiply routine on all the processors (which divides them into two parts: workers and verifiers).  We are grateful to the PIDGIN group for letting us use their Linux cluster and we extend thanks to Daniel Marques for getting us started.  Our experiment ran on Red Hat Linux cluster with five nodes.  The first computer in this group (and the login computer) is considered the master computer, which had two Pentium II processors running at 300MHz with 256MB of RAM.  The four remaining worker computers were each equipped with a single Pentium Pro running at 200MHz with 64MB of RAM.  (Certainly, it would have been nice to let the workers have more processing power, but this was out of our control.)  Lastly, the MPI package we used was LAM-MPI, developed at the University of Notre Dame.

Results

To observe the overhead involved in calculating and comparing checksums, we ran several test cases.  The first, in which we ran one copy of a matrix-matrix multiplication on two processors, served as our baseline for comparisons.  The second test case involved running two copies of the same matrix-matrix multiplication, with two processors devoted to each copy.  From this case we observed a slight overhead which increased as the size of the matrix increased.  For the third case, we ran one copy of the matrix-matrix multiplication, with four processors devoted to the computation.  The expectation was that because of the parallelism, the computation would take half as long to complete when compared with the baseline, and this is what we observed.  These results are summarized in the graph below.

We can quantitatively analyze the overhead involved in parallelizing and replicating our computation.  Suppose we are multiplying together two matrices and that we have copies of the computation with processors devoted to each copy.  Then it would take:

for a total running time of .  This means that with each additional copy of the computation that we introduce, there is an increase in running time of .

Now that we have finished the thrilling analysis of our approach, we would like to consider how this approach would fare for more efficient matrix-multiply algorithms.  The main problem with the simple routine we used was that it is incredibly memory inefficient.  For starters, the entire matrix B is sent to every worker and every verifier.  Preventing this waste of memory is exactly what many people have tried to do.  One of the more popular parallel matrix-multiply algorithms is the Fox algorithm, also known as Broadcast-Multiply-Roll for the steps performed.  This algorithm divides up the A matrix along columns and rows, thus making it nice for the number of available processors to be a perfect square, although not necessary.  The B matrix is similarly divided along rows and columns.  Each worker receives one part of the A matrix and one part of the B matrix.  With these parts, they compute the matrix-multiplication of these two sub-matrices using the normal matrix-multiply routine.  After finishing the matrix-multiply, each processor transfers its part of the B matrix to an adjacent processor that needs it, and the piece of A is transferred as needed as well.  This is called a broadcast.  The multiplication is done on these new pieces, and then rolled into the results of the previous round of multiplication.  This is repeated until the final result is computed, which takes the square-root of the number of available processors iterations to complete.

This is considered a memory efficient algorithm, but it introduces more network traffic — a lot more.  As we noted above, the added cost to our approach is mostly due to network traffic.  If the network traffic is doubled by applying our approach to the Fox algorithm, we could expect much higher overheads than with our simple matrix-multiply routines.  Luckily, there is some hope.  Since the set of verifiers and set of workers need not interact with each other, if they were on separate networks, we could avoid the impact of the added overhead.  As with a lot of considerations for parallel computations, the network topology is crucial.  If interactions among the verifiers is independent from the communication among the workers, we can avoid the overhead incurred by detecting Byzantine failures in the Fox algorithm.  Sadly, this requires control over the network topology which is often too much to ask.  It also requires the compiler to be much more selective about how it divides work between verifiers and workers.

Recovering From Byzantine Failures

So far, we have managed to detect failures.  Now, having detected a Byzantine failure, we need to deal with the problem of determining when the failure occurred.  This can be a non-trivial task, as checksums are imperfect — though unlikely, it is entirely possible to obtain matching checksums for different results. 

There are two approaches to verifying a given computation.  The first is to compare checksums progressively, at various points along the computation.  This has the advantage that if a failure is detected, only part of the computation needs to be redone.  The disadvantage in this approach is that there is added overhead in the frequent checksumming.  The second approach is the one we took, and it is to compare checksums only at the end of the computation.  While this has the advantage of minimal overhead due to checksumming, there is the disadvantage that when a failure is detected, the entire computation would have to be redone.

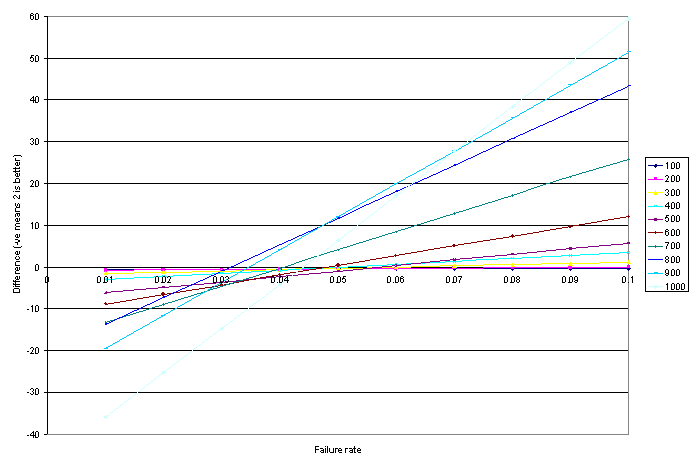
Orthogonal to the issue of verifying computations is the issue of recovery.  Again, there are two approaches.  The first is to create three copies of the computation such that at any given time, we can detect whether any one of the three has failed.  The second approach is to create two copies of the computation and to re-run parts of the computation on an as-needed basis.  The benefit of the former approach over the latter is that if a failure occurs, we don't need to spawn off another copy of the computation and wait for it to complete — we have the information on hand to detect which processor was the faulty one.  On the other hand, the latter approach involves the minimal amount of redundancy needed, and so, more parallelism can be introduced into each copy of the computation.  One would expect that with low rates of failure, the two-copy approach is better, where as the opposite is true with higher rates of failure.  To determine where this transfer point might occur, we analyzed the running time data that we've gathered to come up with an estimate.

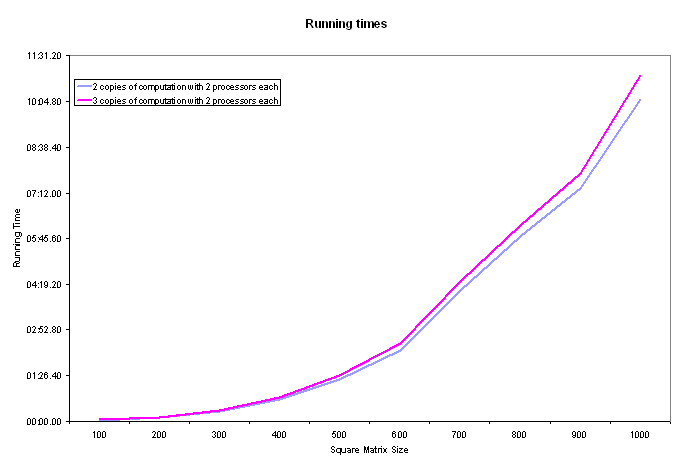
In addition to the three test cases described in the previous section, we ran a fourth test case in which three copies of the matrix-matrix multiplication was run with one processor devoted to each copy.  From the data obtained from this test case, we estimated the running times that we might have obtained if we had the resources to run three copies of the computation, devoting two processors to each copy.  This was done as follows.

From the previous section, the second test case has a running time of , and the fourth test case has a running time of .  The running time for three copies of the computation with two processors devoted to each copy is which we can estimate by using .  Similarly, the running time for the third test case is , and so, we can obtain a second estimate by using .  Making these calculations for each matrix size, there was a discrepancy between the two estimates of at most 5%.  This was judged to be acceptable, so we took the average as our final estimate.  The following graph summarizes the result of these calculations and shows the overhead involved in having three copies of the computation versus having just two.

Now, consider the second test case from above, in which we ran two copies of the computation, with two processors each, and compared checksums.  If the probability of having a given pair of checksums mismatch is , then the cost of having to recompute the result is (in general, it would be , where we have two copies of the computation with processors devoted to each copy).  Hence, on average the overhead for recovery from failures is , or (in general, ).

Using a similar procedure as the one used above, we estimated, for varying failure rates, the running times for having two copies of the matrix-matrix multiplication, devoting two processors to each copy, while recovering from any failures that may occur.  The difference between this estimate and that obtained in the first part of this section for having three copies of the computation is graphed below as a function of the rate of failure.  Negative differences indicate that running two copies results in better performance, while positive differences indicate that running three copies is better.

Compiler Passes

To make the ensuing discussion more lucid, we introduce a small amount of terminology.  First, we want to say that in any computation there is only one set of workers.  The workers compute the whole problem.  Alongside the workers are the verifiers.  In the above description, there is one set of workers and one set of verifiers.  The verifiers never return their results to the master processor, whereas the workers do.

What we are ultimately interested in doing is adding these techniques for detecting Byzantine failures to a compiler transformation.  Aside from the necessity of this (CS612 is after all a course on compilers), this really is a problem that could be solved by the compiler rather than placing the burden on the programmer.  In order to actually make this work, code only needs to be modified in two places: the master needs to send the work to a worker and a verifier, and each processor needs to compute checksums.  Thus, we really only need to find two pieces of code: the code that computes the matrix multiplication and the code that talks to the MPI runtime.

Finding code that computes matrix-multiplication is not difficult, and can be done by pattern-matching on the abstract syntax tree.  Once the matrix-multiply code is found, all that is necessary is introducing an accumulator in the second loop to collect the checksum.  While this is not difficult, we note that placing the checksum code in the middle of the matrix-multiply routine makes it difficult to apply other optimizations to the code.  Finding ways to avoid imperfectly nested loops while keeping the overhead low is attractive.  We will discuss some ways of accomplishing this shortly.

Aside from computing the checksum, we need only modify the communication between the master and the workers.  The first step is finding any calls to the MPI_Comm_size function and adjusting the results of this call such that half as many processors appear available as there really are.  Any communication from the master processor, which is also easy to identify by looking at the processor number in the MPI_Comm_send and MPI_Comm_recv functions, must be duplicated to the actual processor it is intended for and the processor we set aside to be a verifier.  This process only entails duplicating any communication from the master.  After handling communication from the master to the workers, each worker's communication back to the master must be preceded by an extra communication of the checksum to the master.  The master must precede any communication from workers by collecting checksums from the worker and the verifier, and then immediately receive results from the worker.  Verifiers never send anything to the master besides checksums, so this communication must be predicated on whether a processor is a worker or a verifier.  In short, while there is a number of things to do to make detecting Byzantine failures transparent, it is entirely doable.

Now, we return to the problem of perturbing the optimization of matrix-multiply routines.  The first thing that we note is that computing the checksum inside the matrix-multiply loop is not necessary.  Indeed, if we used some other routine to compute the checksum, we could separate the matrix-multiply from the checksum.  This has the added advantage of simplifying the compiler transformation.  Instead, the checksum could be computed immediately before the communication from the worker to the master by running md5 or some similar hash function on the data that the worker intends to send back to the master.  Since md5 runs in linear time, and the amount of data it needs to hash is quadratic (the size of the part of the matrix C), the running time of hashing the matrix into a checksum via md5 is no better or worse than computing the checksum directly in the matrix-multiply loop.  This means a better implementation would likely use md5 to guarantee the communication from the worker to the master is valid.  This also has the added advantage of generalizing our approach, as we are not necessarily searching for matrix-multiply routines and instead we only care about the communication between the master and the workers, or vice-versa.

Final Thoughts

While Byzantine failures do not happen often, there are circumstances where they should be expected such as an untrusted computing environment.  Handling them transparently certainly is practical and, at least to us, an exciting avenue of discovery.  One point we wish to return to is that networks and other mediums of communication now implement error correction codes to prevent against corruption and other errors similar to Byzantine failures.  Even the Pentium III Xeon and Pentium 4 Xeon processors now include error correction codes in the L2 cache.  Verifying the results of a computation in conjunction with these error correcting codes seems interesting and is an area deserving attention.  Unfortunately, we lacked knowledge of some key aspects of these error correction codes to study this possibility effectively.

And finally, we note that halving the number of useful processors is a tall-order for many scientific applications.  Indeed, many end users would prefer to get results earlier than later.  Our technique seems to go against this in many ways.  Nevertheless, we only double the computation time, which by Moore's Law will be fixed in eighteen months anyway. (Slight grin goes here!)  More importantly, combining this technique for detecting Byzantine failures with other fault tolerance failures such as fail-stop seems prudent.  Especially since fail-stop failures are orders of magnitude more likely, adapting them so they also take care of Byzantine failures is in the best interest of consumers in need of fault tolerance.