CS5625 PA2 Mesh Animation

Out: Thursday February 12, 2016

Due: Friday February 26, 2016 at 11:59pm

Work in groups of 2.

Overview

In this programming assignment, you will implement:

  1. blend shapes for facial expressions, and
  2. linear blend skinning for articulated character animations.

Task 1: Blend shapes

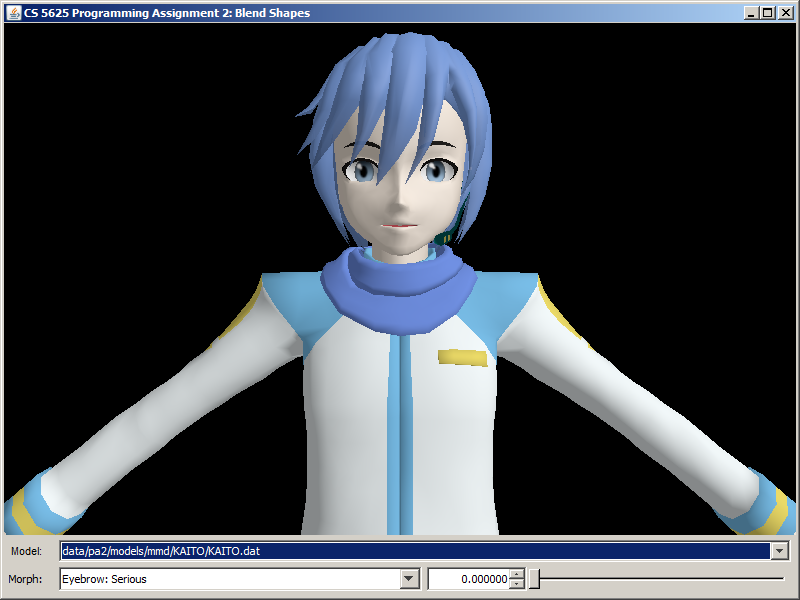
Run the pa2.PA2_BlendShapes class, and you will see that the program allows you to change between three characters:

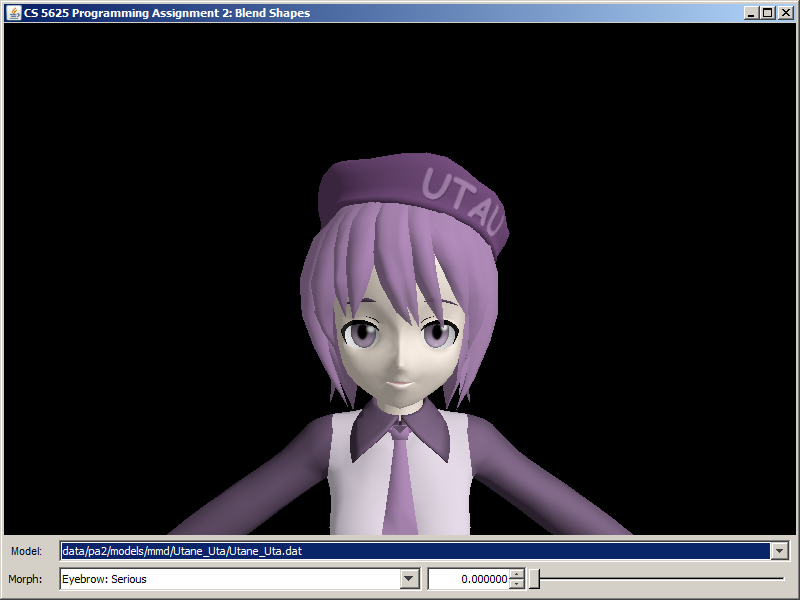KAITO Hatsune Miku Utane Uta

Each charcter has a set of blend shapes or, as we shall call it in this assignment, "morphs," associated with it. A morph in this assigment modifies some facial features of the character, making him/her wink, for example. A specific morph can be selected by the combo box next in the bottom row. Each morph also has an associated "weight," which is a floating point number from 0 to 1. You can set this value using the spinner and the slider in the bottom row.

The basics of blend shapes were discussed in CS4620 in the animation lecture (slides 68–69). The idea is that each vertex comes with a 3D position for each of $N$ blend shapes, and the animation is controlled by per-frame weights $w_j$ for each blend shape, which sum to $1$. If $\mathbf{p}_{ij}$ is the position of vertex $i$ in blend shape $j$, and $w_j$ is the weight of blend shape $j$ in the current frame, then the position of vertex $i$ is $$\mathbf{p}_i' = \sum_j w_j\mathbf{p}_{ij}.$$

Because the blend shapes are the same over most of the character, in this assignment the blend shapes are stored as displacements from a neutral pose; that is $$\mathbf{p}_{ij} = \mathbf{p}_i + \mathbf{d}_{ij}$$ so that the blended position is $$\mathbf{p}_i' = \mathbf{p}_i + \sum_j w_j\mathbf{d}_{ij}.$$ Since the neutral shape has all displacements zero, it can be left out, and the weights no longer have to sum to $1$.

These displacements are zero for most vertices in each blend shape, so for each blend shape $j$ the intput file contains a list of the indices $i$ that have nonzero displacements, with values of $\mathbf{d}_{ij}$ just for those vertices. The data is stored in files like student/data/pa2/models/mmd/KAITO/KAITO.dat; search for the class name SkeletalMeshMorph to see how the data looks. Storing things this way also makes it easy to construct a list of the blend shapes that affect a particular vertex, and to process only those displacements in the vertex shader. The code to read these files and store the data in textures is provided. All this leads to a great decrease in storage and computation, at the cost of somewhat more complex indexing.

For this task, edit:

so that the shader implement morphing of vertices.

Information about morphs come to the shader in pieces of three data structures.

Let $n$ denote the value of vert_morphCount. To compute a morphed vertex position, write a loop that starts fetching the vert_morphDisplacements array at indices vert_morphStart, vert_morphStart+1, vert_morphStart+2, $\dotsc$, vert_morphStart+$n$-1. Each of these texture fetching will give you information about the largest displacement that you can apply to the vertex and the index of the associated morph. Now, with the index of the morph at hand, you can find the weight of the morph from the vert_morphWeights texture. Once you know the weight, scale the displacement by the it and add the resulting weighted displacement to the vertex position. (For morphing, you only change the vertex position and do not have to care about the normal, the tangent, or the bitangent.)

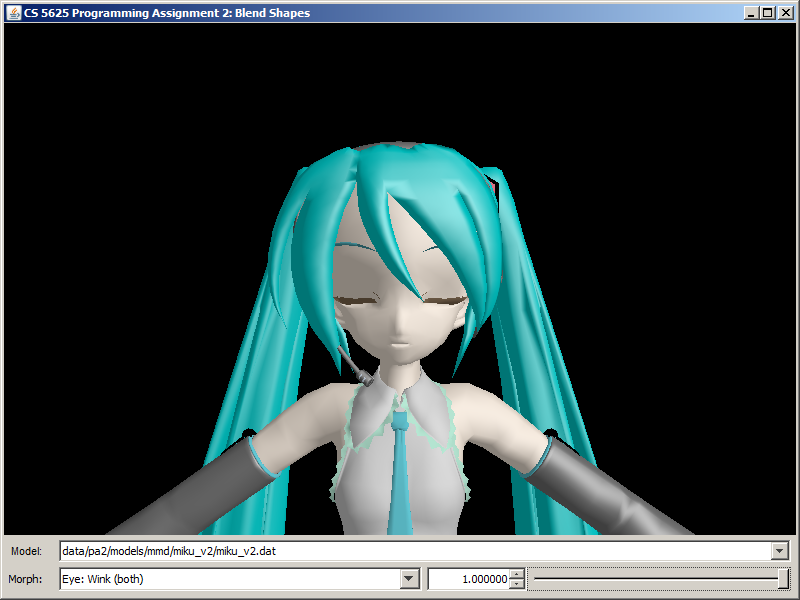
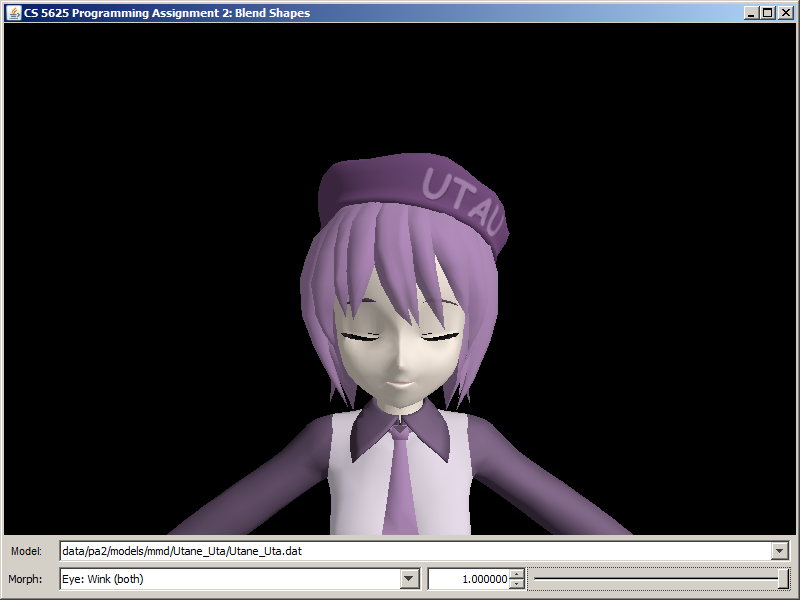
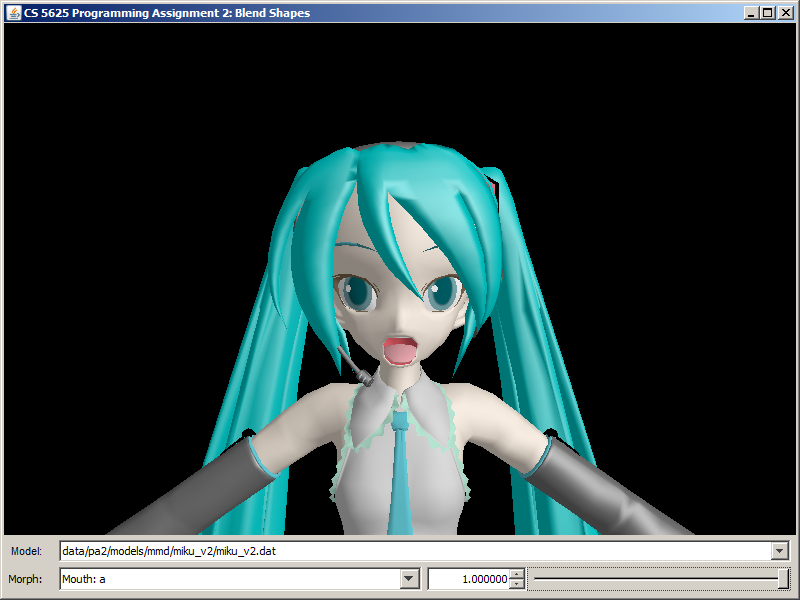
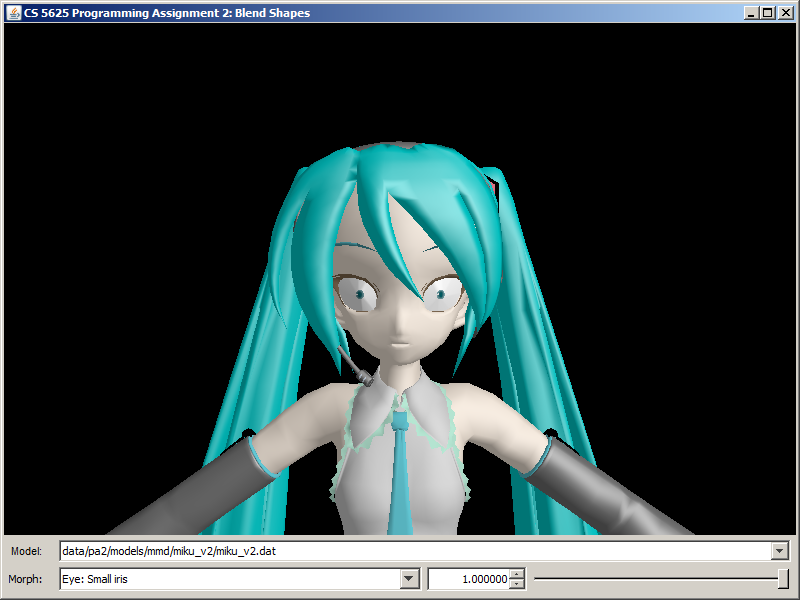
A correct implementation of the shader should yield the following images

Morph KAITO Hatsune Miku Utane Uta
Eye: Wink (both)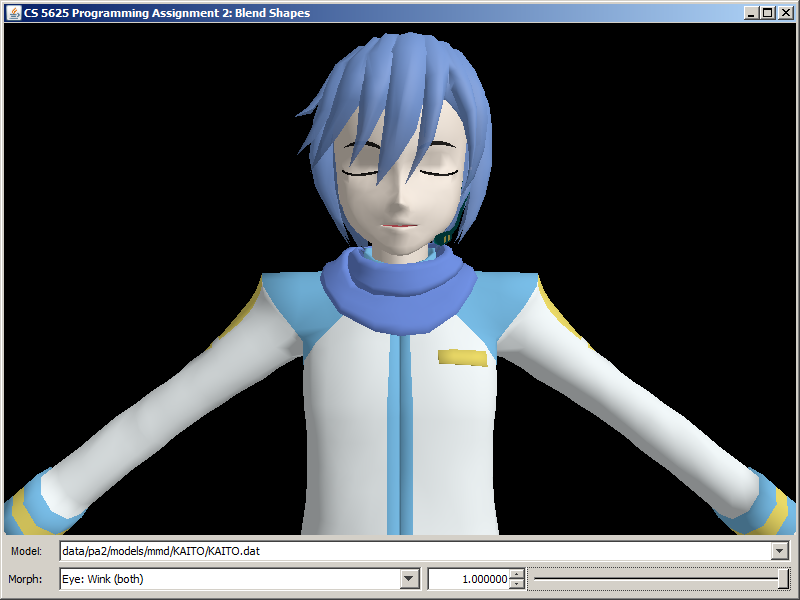
Mouth: a
Eye: Small iris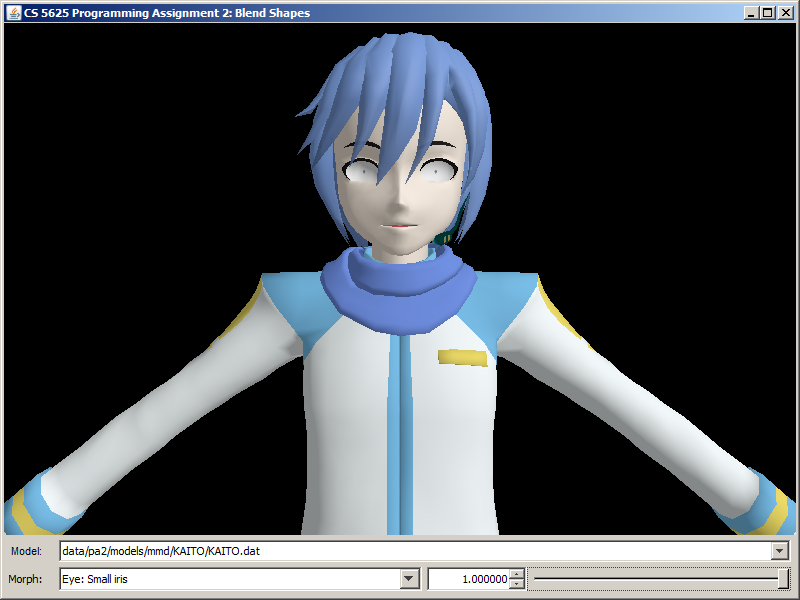

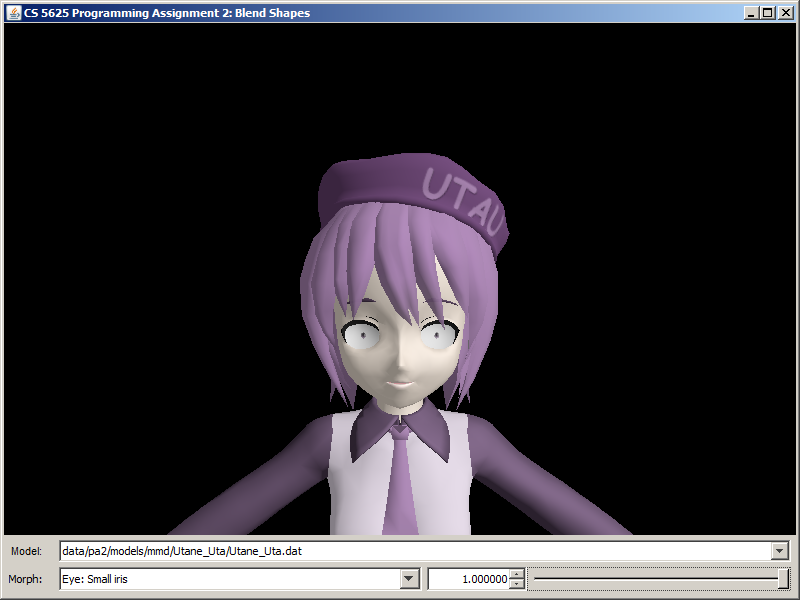Task 2: Linear blend skinning

The last piece of our character animation system is linear blend skinning, a technique that allows vertices of a mesh to deform according to an underlying skeleton. Linear blend skinning is discussed in slides 62–67 of the CS4620 animation lecture. The basic idea is that the pose of an animated character is specified by using per-frame linear transformations (usually rigid) for each of a set of bones in the skeleton, and the deformed positions of the mesh (the "skin") are computed by applying a combination of the bone transformations to the neutral vertex position. The influence of bone $j$ on vertex $i$ is given by a fixed (not per-frame) weight $w_{ij}$, so the deformed position is: $$\mathbf{p}_i' = \sum_j w_{ij} \mathbf{P}_i.$$ Since each vertex is normally influenced by only a few bones, in this assignment we store the weights for a vertex $i$ by keeping a list of the bone indices $j$ for which the weights $w_{ij}$ are nonzero, togther with the values of those weights. Each vertex is only allowed to be influenced by up to four bones, so we store exactly four indices for each vertex, using the value $-1$ to indicate an unused index. You can see an example of the input data in the file student/data/pa2/models/mmd/KAITO/KAITO.dat, in the fields boneIndices and boneWeights of the ConcreteSkeletalMesh.

The animation data for each frame consists of a bone transformation for each bone and a morph weight for each blend shape; only nonzero morph weights are stored. See for example the single-frame animation in student/data/pa2/motions/KAITO/stand01.dat.

For this task, edit:

to implement it.

The SkeletalMeshPoseManager class manages the "pose" of an articulated mesh. A pose is basically the collection of morph weights (each a floating point number from 0 to 1) and the configurations of skeletal bones (each bone has a corresponding displacement and a rotation). The morph weights are stored in the morphWeights field. The bone displacements and rotations associated with the pose are stored in the boneDisplacements and boneRotations fields, respectively. Morph weight processing has been completely implemented, so you do not need to worry about it. However, you will need to implement the computation of transformation matrices for each bone in this task.

The method updateBoneXformTexture computes for each bone a transformation matrix for use with linear blend skinning and stores the result in the boneXforms field so that the $i$th element stores the matrix for the $i$th bone. The bones themselves are stored in the bones field. Each bone is represented by the SkeletalMeshBone structure, and it has two piece of important information:

We now discuss the computation of the matrices for linear blend skinning. Let:

Now, let us say that we are interested in Bone $i_k$, which is a child of Bone $i_{k-1}$, which in turn is a child of Bone $i_{k-2}$, and so on until we reach bone $i_0$ which does not have a parent. The matrix for linear blend skinning can be computed in two steps:
  1. First, compute the 4x4 transformation matrix associated with the translation from the origin to the world position of Bone $i_k$ in rest position. This matrix is given by: $$M^{\mathrm{R}}_{i_k} = T^{\mathrm{R}}_{i_0} T^{\mathrm{R}}_{i_1} T^{\mathrm{R}}_{i_2} \dotsm T^{\mathrm{R}}_{i_{k-1}} T^{\mathrm{R}}_{i_k}.$$
  2. Second, compute the 4x4 transformation matrix associated with going from the origin to the world position of Bone $i_k$ according to the pose. This matrix is given by: $$ M^{\mathrm{P}}_{i_k} = ( T^{\mathrm{R}}_{i_0} T^{\mathrm{P}}_{i_0} R^{\mathrm{P}}_{i_0} ) ( T^{\mathrm{R}}_{i_1} T^{\mathrm{P}}_{i_1} R^{\mathrm{P}}_{i_1} ) \dotsm ( T^{\mathrm{R}}_{i_{k-1}} T_{i_{k-1}}^{\mathrm{P}} R_{i_{k-1}}^{\mathrm{P}} ) ( T^{\mathrm{R}}_{i_k} T_{i_k}^{\mathrm{P}} R_{i_k}^{\mathrm{P}} ). $$
  3. The bone matrix for linear blend skinning is then given by: $$ M_{i_k} = M^{\mathrm{P}}_{i_k} ( M^{\mathrm{R}}_{i_k} )^{-1}. $$

After you have computed the matrices, the rest of the updateBoneXformTexture will take care of sending the information to the shader for you. The next part of this task is to write the shader to make use of this information. In skeletal_mesh.vert, we have provided the getBoneXform function such that calling getBoneXform(i) fetches the matrix boneXforms.get(i) that you previously computed.

To perform linear blend skinning, we first morph the vertex according to the blend shapes as was done in the last task. Let us denote the morphed vertex position by $\mathbf{p}$. The vertex can be influenced by a number of bones, and each of this bone has different amount of influence on the vertex, indicated by the bone's weight. The indices of the bones that influence the vertex is stored in the vert_boneIndices attributes, a vec4, meaning that there can be at most four bones that can influence the vertex. You can retrieve the index of the $j$th bone with the expression vert_boneIndices[j] where $j$ ranges from 0 to 3. Some of these indices may be -1, indicating that this is not a valid bone and should be ignored. The weights of the bones are stored in the attribute vert_boneWeights, and the weight of the $j$th bone can be retrieved by the expression vert_boneWeights[j]. Now, suppose that the indices of the bones are $j_0$, $j_1$, $j_2$, and $j_3$, and the associated weights are $w_{j_0}$, $w_{j_1}$, $w_{j_2}$, and $w_{j_3}$. Then, the linear blended vertex position is given by: $$ \mbox{blended vertex position} = w_{j_0} M_{j_0} p + w_{j_1} M_{j_1} p + w_{j_2} M_{j_2} p + w_{j_3} M_{j_3} p.$$ Now, you also have to compute the blended tangent, bitangent, and normal. We suggest that you compute the tangent and bitangent using the formula similar to the above. Then, you can compute the normal by computing the cross product between the two vectors.

Lastly, note that the positions and tangent frame you computed in the last paragraph are in object space. You have to transform them with the appropriate matrices to pass them to the fragment shaders and the rasterization unit. However, the code to do this has already been provided for you in the shader.

You can test the full implementation of the character animation system by running the pa2.PA2_Animations class. Here, you still have the option of selecting among the three characters, but you can also subject them to 5 poses/animations. A correct implementation of the system should produce the following images:

Animation/Pose KAITO Hatsune Miku Utane Uta
Stand 1
Stand 2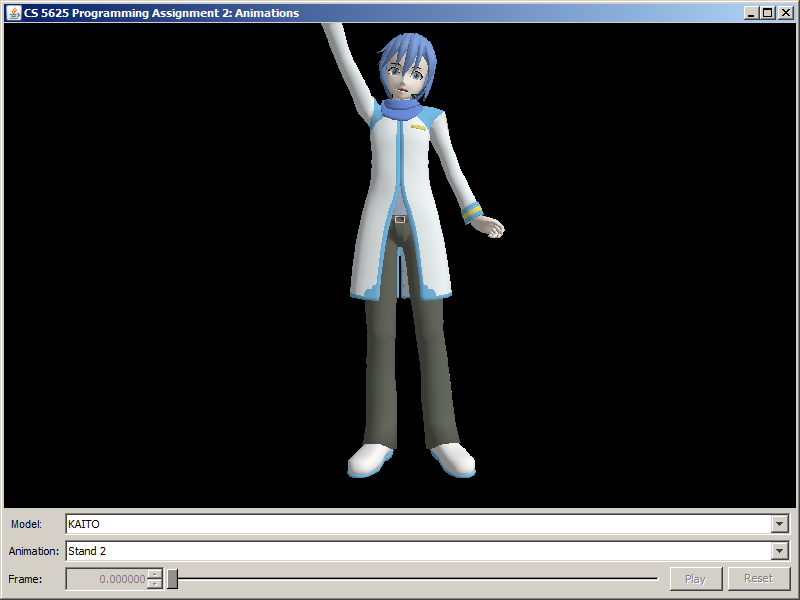
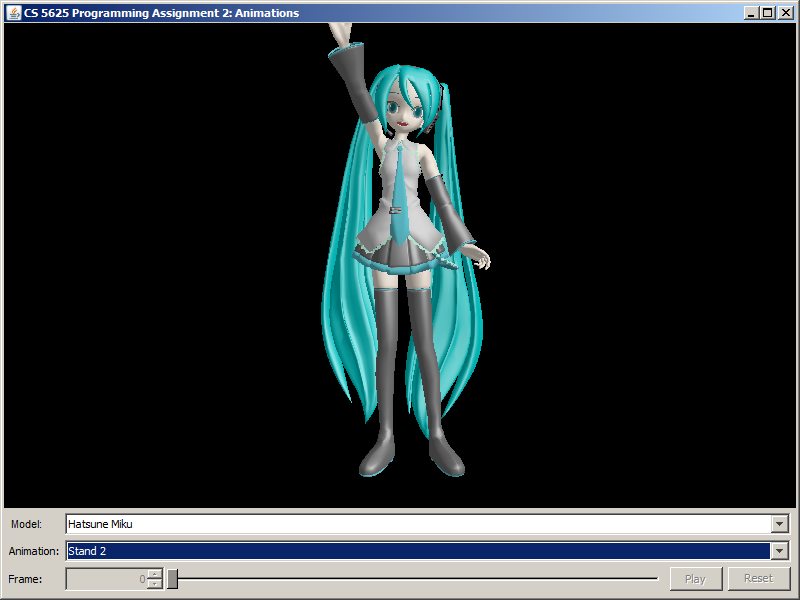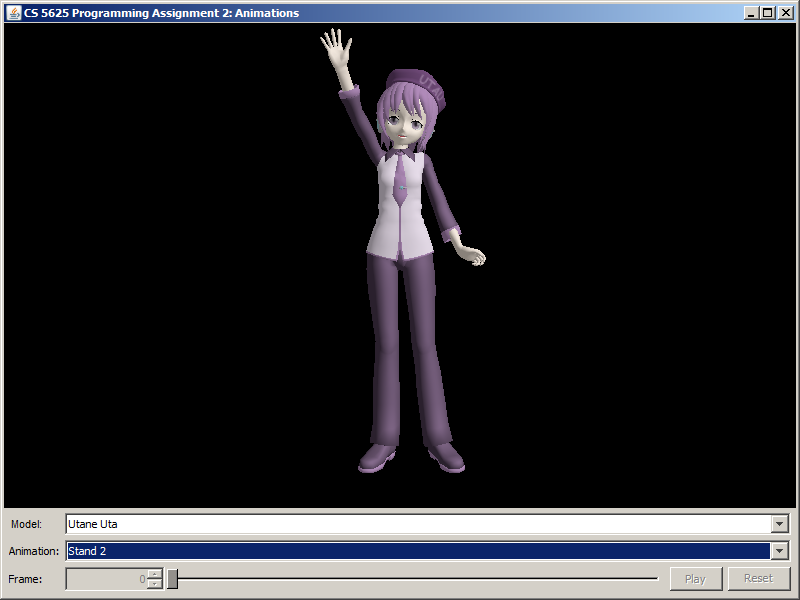Stand 3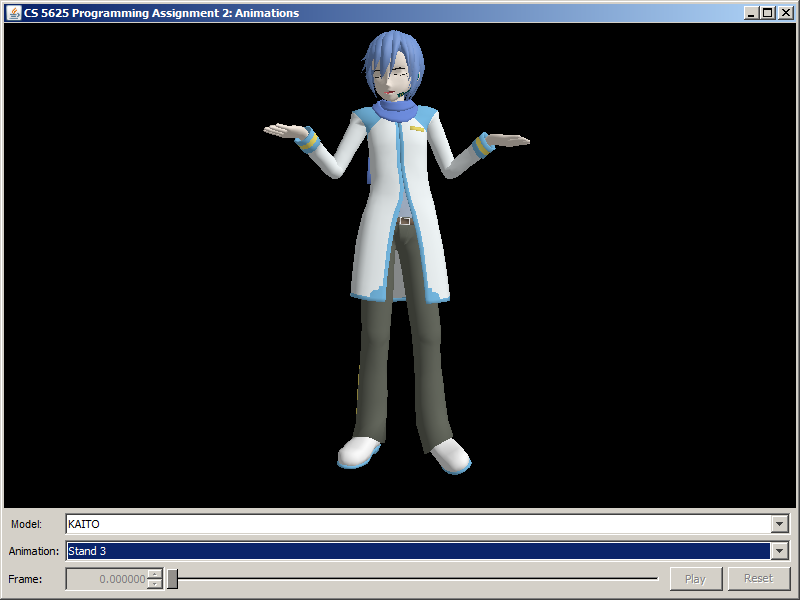
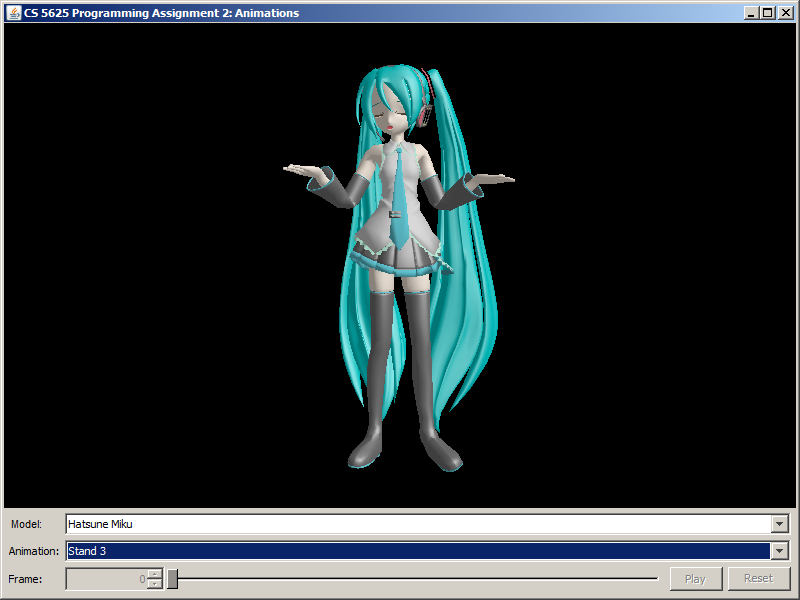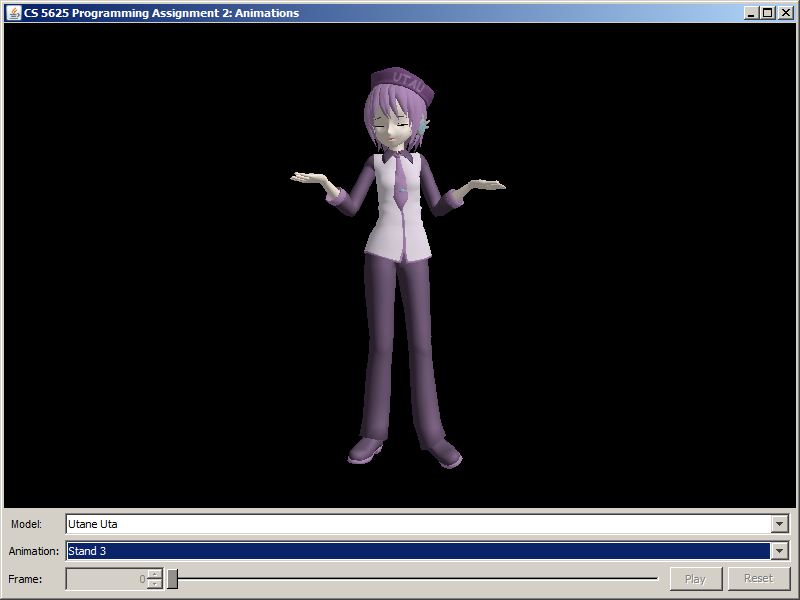Suki Yuki Maji Magic! (frame 3,000)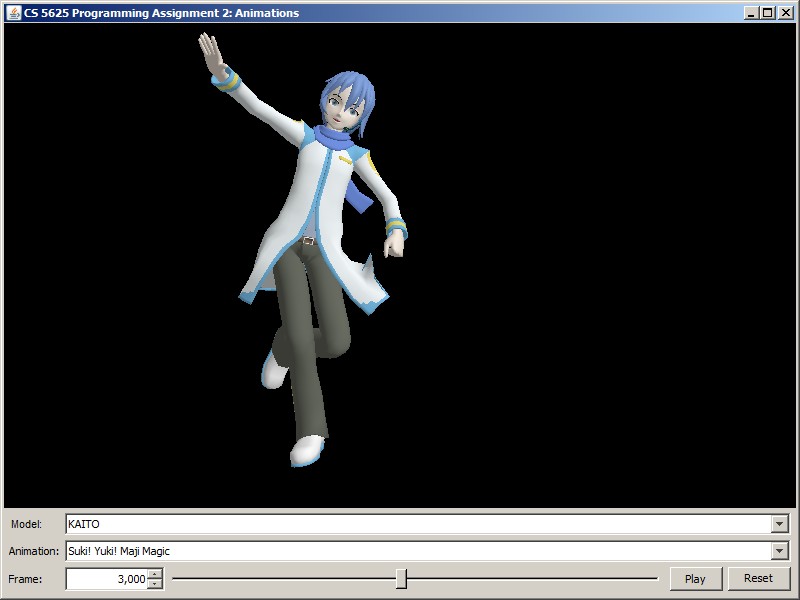
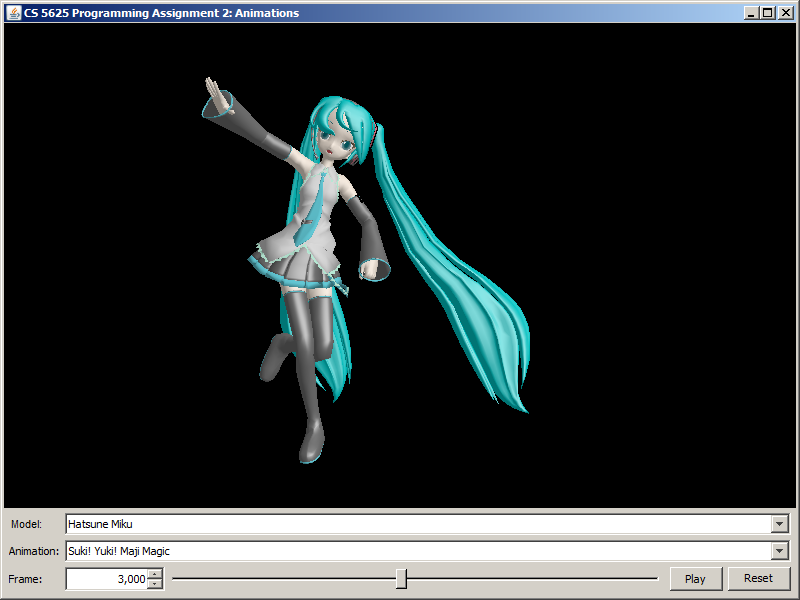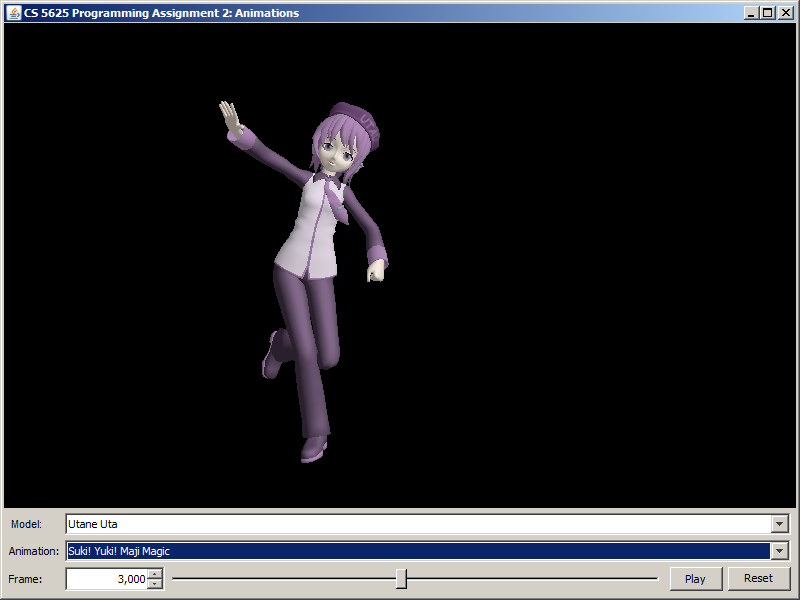Neko Mimi Switch (frame 3,000)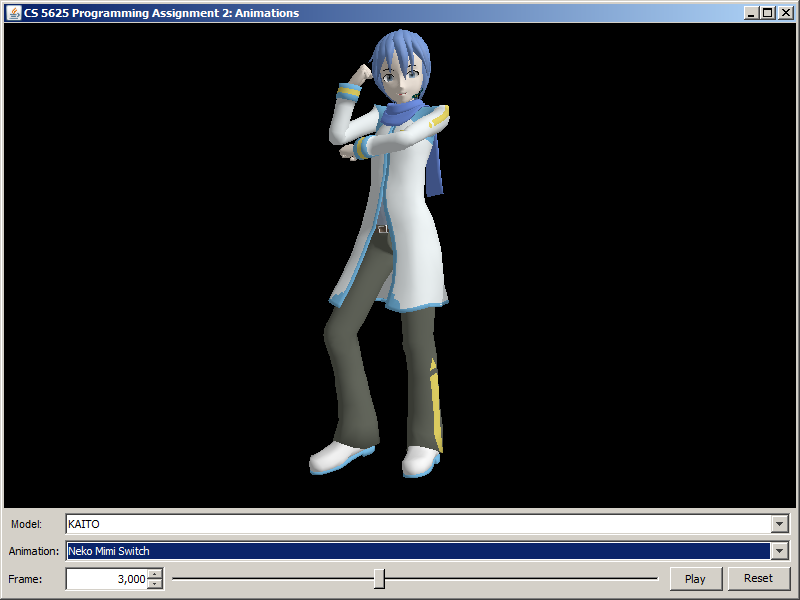

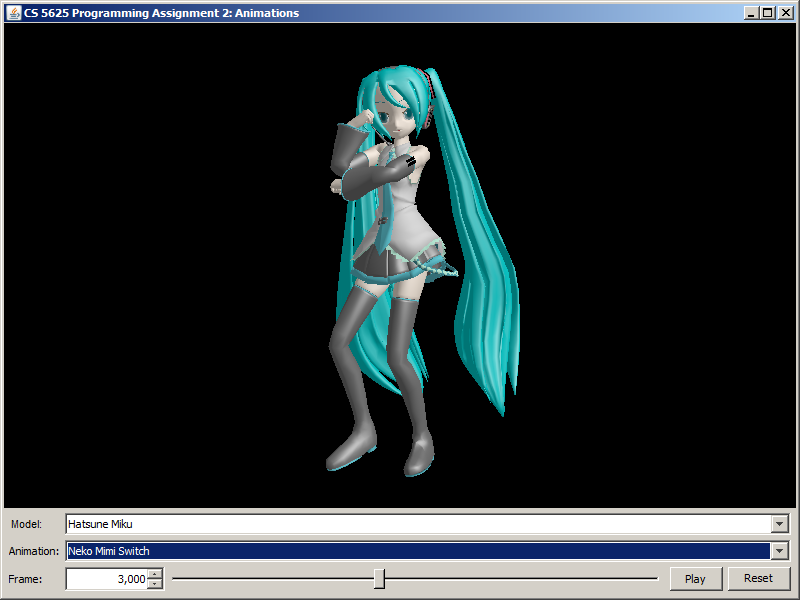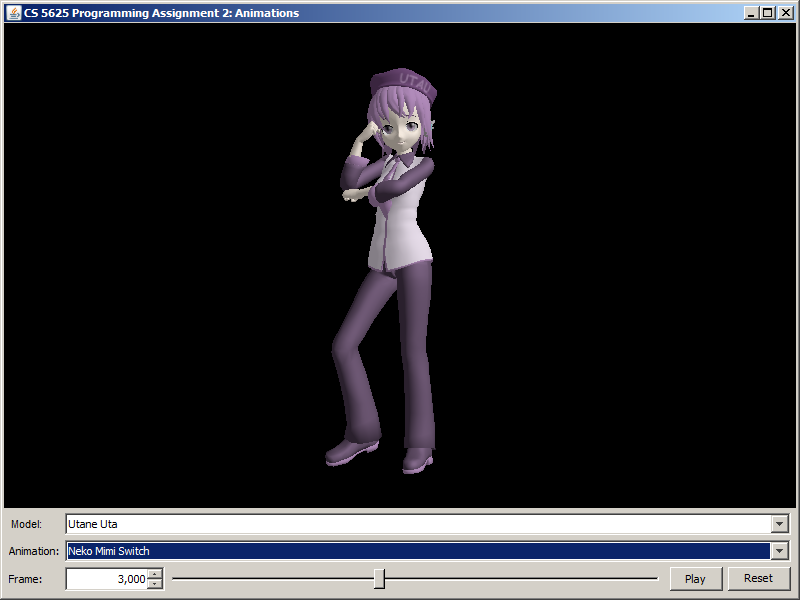For your reference, see the following Youtube videos for the full Suki Yuki Maji Magic! and Neko Mimi Switch motions.

Lastly, run pa2.PA2_DanceScene to see two characters dance as a duet. This scene uses the Blinn-Phong material, so make sure that you edit pa2.ForwardRenderer so that it can use the material as well.

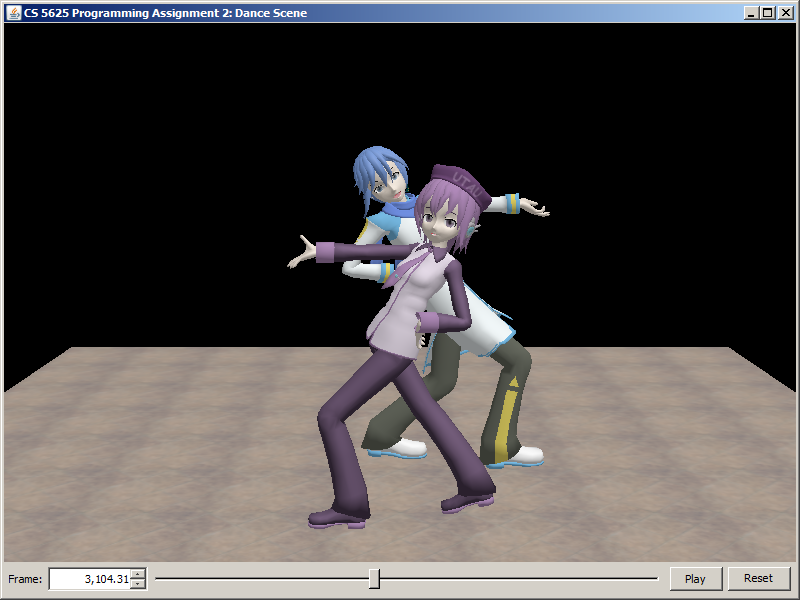Credits and Copyrights

The character models used in this assignment were originally designed to be used with the MikuMikuDance animation software. The KAITO and Utane Uta models were created by マシシ, which, as far as I (Pramook) understand from his/her homepage, is OK with modification and redistribution of the models. The Hatsune Miku model was created by あにまさ. The model was distributed together with the MikuMikuDance software, and it seems to be editable and redistributable. The character KAITO and Hatsune Miku are copyright of Crypton Future Media Inc. They seem to be permitting the characters to be used for educational purposes.

The Stand 1, 2, and 3 poses were taken from a collection of poses created by ゴロゴロウ, who generously allow the poses to be used even for commercial purposes. The Suki Yuki Maji Magic and the Neko Mimi Switch motions were created by hino, who allows the motions to be used for non-commercial purposes and redistributed. The motion for the dance scene is one for the song 恋は気まぐれイリュージョン！！ and was created by CRACKDOWN, who allows the data to be modified and redistributed for non-commercial purposes as well.

We are grateful of all the creators for their efforts and setting permissive conditions for reuse of their works.