
Lecture notes by Tom Roeder, Michael Clarkson and Deniz Altinbuken
For example, suppose that Alice visits a web site that plants a Trojan horse in her browser, which attempts to copy her secret data up to a public web site. Alice would like the system to enforce a policy that data she labels secret must not become public. Of course, this is harder than it seems. You might imagine a naive solution: monitor the outgoing network link from the browser, and disallow transmission of bytes that look like the secret data. However, we can't tell a priori what is secret and what isn't, in part because data can be encoded. For instance, the Trojan horse might encrypt the data, so that the bytes no longer look like Alice's data. Or, the Trojan horse might use a different network connection than the browser's, perhaps by sending email.
The problem becomes even worse, since data is just bits, and there are many devious methods for transferring bits. For example, a sender (perhaps a Trojan horse) can create a file in a temporary directory, and a receiver can attempt to access this file at regular intervals. At each interval, if the attacker wants to send '1', he locks the file, and if he wants to send '0', he doesn't. The receiver can tell by trying to access the file whether or not it is locked, so we have succeeded in transmitting a single bit, and the process can be repeated to transfer data at a potentially high rate. A similar method uses system load to transfer information. The attacker uses many cycles to send a one, and uses few cycles to send a zero. This is a noisy medium for transmission, since other programs are also using the CPU, but data transfer in the presence of noise is a well-studied problem in the field of information theory. The moral is that data can be transferred by abusing mechanisms in ways that designers never intended.
All these examples use channels to transmit information. A covert channel is one in which data is encoded into a form, such as timing, not intended for information transfer.
Toward our goal of enforcing end-to-end security, we examine a class of policies called information flow policies. These policies restrict how information flows through a system, that is, they control the release and propagation of information. A familiar kind of information flow policy is a confidentiality policy, which specifies what information can be disclosed to whom. The goal of such a policy is to prevent information leakage, or the improper disclosure of information. Alice's policy in the example above is a confidentiality policy.
In the rest of this lecture, we consider one particular confidentiality policy, known as noninterference (NI). This policy was originally formulated in terms of groups of users in a shared system, such as Unix or a database. Noninterference requires that the actions of high-level users have no effect on (i.e., should not interfere with) what low-level users can observe. We will adapt this policy to a programming language.
Suppose that all variables in our programming language are labeled with either S or P, which correspond to secret information and public information, respectively. We write xS and yP to indicate that the variables have the given security label. The variable s is, by convention, a secret variable; similarly, p is public. The label of a variable is fixed and cannot change, either in the program text or during execution.
We want to enforce the policy that information does not flow from secret to public variables. Immediately, we notice that we can determine the security of two simple programs.
The first program is secure because information flows from a public variable to a secret variable, which does not violate our policy. But the second program is insecure because it does violate the policy: information flows from a secret variable to a public variable. In this program, if s were initially equal to 0, then upon termination of the program, p would equal 0. But if we changed s to initially equal 1, then p would also equal 1. So this program violates noninterference because secret information has an observable effect on public information.
More generally, we can represent the execution of the program as a box with public and secret inputs and outputs. The possible information flows through the program are represented here with arrows from input variables to output. There is only one flow disallowed in the execution of this program, and that is the flow from Sin to Pout:

We define noninterference as changes in S inputs do not cause changes in P outputs. Suppose that the program, represented by the box below, satisfies noninterference. We can then consider what the possible outputs would be if Pin remained constant and Sin changed. Since the only difference in the two executions of the program is the initial values of secret variables, the output values of public variables cannot be different. Sout, however, can be changed, since noninterference does not put any restrictions on the output of secret variables.

Here are some example programs:
p = p + s;
This program does not satisfy NI. For instance, if we start with p = 2 and s = 4, we get output p = 6. If we change the secret input to s = 14, we get output p = 16, so S is interfering with P.
s = p;
This program satisfies NI, because the changes in P inputs cause changes only in S outputs, not P outputs.
p = s;
p = 1;
After the first statement, there is interference, but the second statement writes over p, and thus the program as a whole satisfies noninterference.
if (s mod 2) = 0 then p = 0; else p = 1;
This program doesn't satisfy NI as the parity of s, which should remain secret, determines the value of output p.
while (s != 0) do { //nothing }
This program leaks information through covert channels because termination of the program would reveal information about s. But changes in S inputs do not cause changes in P outputs here, so this program satisfies NI.
The third example raises an interesting question: what if the attacker could observe the value of p during execution of the program? Then we would not be able to claim that this program satisfies noninterference, because a change in s would be observable. The problem of protecting a process's memory is orthogonal to the problem of enforcing noninterference, so we will make the assumption that the values of public variables are only observable immediately before execution begins, and immediately after termination if the program terminates. The values of secret variables are never observable by an attacker.
Information flow can also result from control flow; we call this implicit flow. This is depicted in example four, as the parity of s is leaked, even though there is no direct assignment from s to p. The opposite of implicit flow is explicit flow, of which program 1 is an example.
We want to enforce noninterference while still allowing interesting interactions between public and secret variables in our programs. If we were willing to be more draconian, we could consider separating programs into two halves, one which references only secret variables, and one which references only public. It is clear, however, that such separated programs do not allow many useful computations, such as computing functions of both secret and public data, or secret logs of public data. There are two standard ways to enforce properties of programs:
Let us consider whether these can be used to enforce noninterference.
An interpreter reads the instructions in a program and simulates the execution of each instruction. Consider what an interpreter should do for each of the following statements:
Does not violate noninterference: execute it.
Does not violate noninterference: execute it.
Does not violate noninterference: execute it.
This statement must not be executed by the interpreter, since it leaks secret information into a public variable. There are two possible actions that the interpreter can take here. One is to terminate the program, and the other is to skip the instruction. The latter approach was taken in the Data Mark machine [Fenton 1977]. But it is difficult to write correct programs when assignment statements may be skipped. Thus, the standard action for an interpreter is to abort the program.
Suppose that s = 1. Then the execution of this assignment leaks information, just as our earlier example of implicit flow did. So according to our reasoning above, the interpreter must abort execution of this statement. But when can it securely abort? Aborting after execution of the assignment is insecure, because an attacker could infer that s = 1 from the fact that an abort occurred. The only other possible option is to abort before evaluation of the guard. Unfortunately, this eliminates many useful programs, since we could never test the values of secret variables. The problem here is that when it comes time to execute the if statement, it is already too late to prevent information flow.
Now we will show how to build a type system that can statically enforce noninterference. A type system is a set of inference rules. The syntax of the program usually dictates which rule should be applied.
The inference rules are used to derive typing judgments. Inference rules are usually written in the following form:|
Assumptions |
|
|
| Conclusion |
Assumptions are sometimes called premises.
For example, the following inference rule states that if the type of variables x and y is int, then their addition is also of type int:
|
x: int y: int |
|
|
| x+y: int |
But how do we know the types of variables? Typing judgments can include typing contexts to record the types of variables. In the following notation, Γ denotes the typing context, where "Γ(x) = int" means "x has type int" and "Γ ⊢ x+y: int" means "context Γ proves that expression x+y has type int".
|
Γ(x) = int Γ(y) = int |
|
|
| Γ ⊢ x+y: int |
Now we define our type system for noninterference. This type system was first defined by Volpano, Smith and Irvine (1996). In this type system a variable can either be of type S or P:
The following typing judgment means that expression e contains information with secrecy level τ or lower:
For example, after recording variable declaration "P x; " the context will be updated to include
The corresponding inference rule that gives the type of the variable x is
|
Γ(x) = τ |
|
|
| Γ ⊢ x: τ exp |
Axioms are inference rules with no assumptions. In our type system we have the following axiom for all integers n, as all integers are public information.
|
|
| Γ ⊢ n: P exp |
For addition expressions the following inference rule ensures that information flows only between expressions of the same type:
|
Γ ⊢ e1: τ exp Γ ⊢ e2: τ exp |
|
|
| Γ ⊢ e1+e2 : τ exp |
A similar rule can be used for any arithmetic expression, such as subtraction, multiplication, etc.
Now let's see how we can use this inference rule to prove that s1+s2 is acceptable by our type system, where s1 and s2 are both S variables, by building the corresponding proof tree:
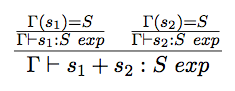
Note that this inference rule doesn't allow s+p. To be able to handle expressions that include different types we have to define subtyping relations.
Type τ is a subtype of τ', denoted τ ≤ τ', if anywhere a program expects a value of type τ', a value of type τ could be used instead. For example, String ≤ Object holds in Java, because a String can be used anywhere an Object is expected.
In our type system we want the subtyping relation to be P ≤ S. This relation allows the secrecy level of a variable to be increased (from P to S) and prevents it from being decreased (from S to P). The inference rule for subtyping is
|
Γ ⊢ e: τ exp τ ≤ τ ' |
|
|
| Γ ⊢ e: τ' exp |
Using this inference rule in our typing system, now we can type check s+p:

So far all our typing rules have been for expressions. An expression is any mathematical function constructed using program variables and built-in operators, such as 3*y+z. We give an expression e a type τ exp, which means that e contains information with secrecy level τ or lower. Next, we turn to typing rules for commands.
We introduce a new type for commands, denoted τ cmd. A τ cmd assigns only to variables of secrecy level τ or higher. Note the asymmetry between τ exp ("τ or lower") and τ cmd ("τ or higher"). The typing rule for assignment commands is
|
Γ(x) = τ Γ ⊢ e: τ exp |
|
|
| Γ ⊢ x:=e : τ cmd |
In some cases an assignment might not violate noninterference but the typing rules may reject it. Thus, our type system is conservative. If we can derive that a program is secure, then the program satisfies noninterference; but if we cannot, then we don't know whether the program satisfies noninterference. The problem is that our rules are too weak to recognize all noninterfering programs. This may seem strange, but you are, in fact, accustomed to such conservative type systems from normal programming languages. For example, the code
will not compile in Java because of a type error, even though the error will never occur in any execution of the program.
The rule for if commands is
|
Γ ⊢ e: τ exp Γ ⊢ c1: τ cmd Γ ⊢ c2: τ cmd |
|
|
| Γ ⊢ if e then c1 else c2 : τ cmd |
We also need a rule for command subtyping to allow different branches of an if command to assign to variables of different security levels.
|
Γ ⊢ |
|
|
Γ ⊢ c : τ' cmd |
Note that subtyping for commands is different than subtyping for expressions.
The rule for sequences of commands is
|
Γ ⊢ c1: τ cmd Γ ⊢ c2: τ cmd |
|
|
| Γ ⊢ c1;c2; : τ cmd |
Loops are like if statements with a single branch.
|
Γ ⊢ e: τ exp Γ ⊢ c: τ cmd |
|
|
| Γ ⊢ while e do c : τ cmd |
There is an interesting quirk lurking in this rule. Consider the following code:
p = 0;
while (s = 0) { }
p = 1;
Our rule says that this program is secure. However, if
this program has not terminated after a long time, then an attacker can infer
that s is likely to be 0. The problem with the rule we gave
is that it is termination-insensitive, that is, it ignores information flows through termination channels. Termination
is a covert channel, similar to a timing channel. Whether or not this matters depends on
an aspect of the execution model which, until now, we have left undefined:
whether it is synchronous or asynchronous. In a synchronous
model, observers have access to a clock, and also have some bound on the
time which the program will require to terminate. This allows an observer to
detect whether the execution has exceeded that bound, and thus entered a
nonterminating state such as an infinite loop. In an asynchronous model,
we assume that observers do not have access to a clock. Without a clock, an
observer cannot detect nontermination. We conclude that in the asynchronous
model our rule enforces noninterference, but that in the synchronous
model it does not.
Our type system may accept or reject a program. If a program is accepted, it satisfies noninterference but it might leak information through covert channels, as demonstrated by the while example above. If a program is rejected, it might or might not violate noninterference, as demonstrated by the if example above. When the type system accepts a program that actually leaks information, we say that a false negative has occurred. And when the type system rejects a program that actually doesn't leak information, we say that a false positive has occurred.
The following table summarizes this state of affairs.
| Leaks information | Doesn't leak information | |
| Rejected | violates noninterference | false positive |
| Accepted | false negative | satisfies noninterference |
False positives and false negatives are standard problems with any compiler analysis.