Lecture notes by Lynette I. Millett
The question is: How can we check the program? This is equivalent to proving a theorem, namely: the program does not read/write/jump outside of its LFD. However, we don't want the operating system to have to construct this proof for each program. Moreover, some things are impossible to prove (e.g. we can't prove a program does not halt). The solution is to expect the program to be accompanied by its proof. Now, we only need check that the proof is valid, and that is a reasonable task for an operating system's loader. We demonstrate how this can be done for a simple flow-chart programming language.
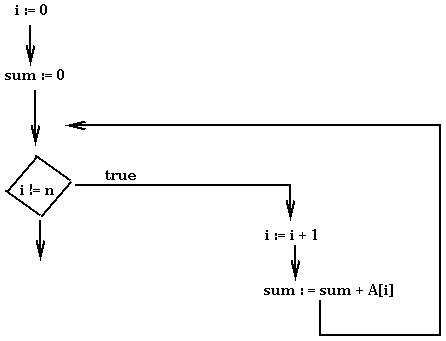
Consider the following program:

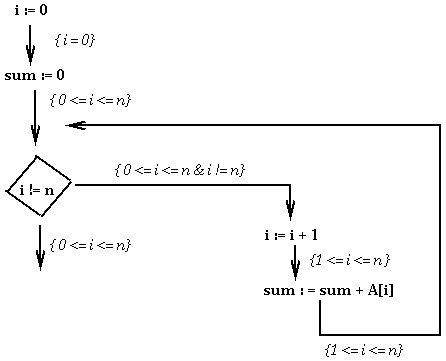
In the example, the annotations constitute a proof that all accesses to array A are within range. We now discuss how to check such a proof. This entire method is referred to as proof-carrying code (PCC) because we transmit a program with its proof to a checker that then decides whether to run it or not. How the checker works depends on the language used. We will consider proofs at the level of assembly language. In this scenario, a proof can be decomposed into two kinds of elements:

Let's consider the decision box. In order to check this, we need to check that the 'B' on the out edges is equivalent to the 'B' in the box. A more general case would be:
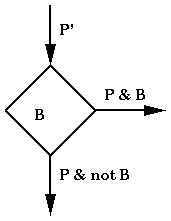
For the assignment box, we need to check that P implies Qex, where Qex is defined to be Q with all instances of x replaced by e. As an example, consider the following:

We now consider the relationship between SFI and PCC. Suppose we are given a program. After running it through SFI we obtain a program that has a lot of additional code. If we now put this transformed program through an optimizer, the optimizer will likely eliminate some of the additional code. In order to trust the optimized SFI'd code, the optimizer now needs to be a part of the TCB. If the optimizer can provide a narrative about what it did to the program, then the optimizer need no longer be part of the TCB. Instead we can add to the TCB a checker that evaluates the narrative to make sure the optimizer only removed gratuitous checks. The narrative is, in essence, a proof. PCC and SFI are clearly related. The former does analysis and the latter adds instructions to the program. SFI provides a program that is very easy to check the proof for.
