Lecturer: Tom Roeder
Lecture notes by
Tom Roeder
Cryptographic hash functions are zero-key cryptographic functions that have strictly stronger properties than one-way functions. They take a variable-length input and produce a random-looking fixed-length output. The requirements on cryptographic hash functions vary from application to application; it is important to ensure that the requirements match what the function actually produces.
As an example of the application of cryptographic hash functions, consider the following game: two players compete to state the highest number. If one player hears the other's number before stating his, then he has an advantage, since he can always state a higher number. One way around this problem is for the players to commit to their numbers before stating them. First they each state their commitments, then they each state their numbers. Once a player has committed to one number, the commitment scheme should not allow him to find another number that also matches his commitment. Otherwise, this player might be able to find a higher number that matches the commitment and perform the same attack as before. This commitment scheme should also hide the values of the numbers.
Cryptographic hash functions are compression functions. Function h is a compression function if h takes a variable length input to a constant-length output.
∀ x: |h(x)| ≤ n.
(Note that |h(x)| < n need only hold when |x| < n) Compression functions are valuable in settings where summaries of information is needed. Such summaries are often called message digests or fingerprints. Note that these compression functions, unlike the compression functions we normally consider (e.g., the compression functions used in telecommunications or music), are inherently lossy, since they compress arbitrary bit strings to a fixed length. This loss need not be a significant concern in practice. For instance, if n = 160, then there are 2160 possible outputs of the compression function. Even though this number is smaller than the space of all possible messages, it should be feasible to design functions that spread messages so evenly over the space that it is extremely unlikely that any inputs that compress to the same output could be found.
Note, however, that a compression function says nothing about hiding its input given its output or making its output pseudo-random. In fact, a trivial compression function simply truncates its input to n bits.
Collision Resistance is a requirement on the relationship of inputs and outputs that is similar but stronger than one-way functions.
We define collision-resistance over a family of functions instead of a single function because every compression function has collisions (by the pigeon-hole principle, since compression reduces the size of the range of the function to be smaller than the domain), so requiring that no adversary be able to find a collision is too strong a definition; there always exists some adversary that happens to know a collision. Families of functions, however, can be designed so that it is hard even to know a single collision for every function in the family, since there can be exponentially many functions in the family. The following properties define a family H of collision-resistant hash functions. We assume the existence of a simple way to choose a member of H.
Collision-resistance implies a weaker property that is sometimes assumed instead:
Properties 3, 4, and 5 all present different variants of hardness for finding collisions in hash functions. But none of these properties guarantee that from the output of a function it is hard to deduce anything about its input. We get this property from pseudo-random functions, but we would like a function that requires zero keys. Solutions to this problem exist and are called Perfectly One-Way functions; describing the reasoning behind these algorithms is out of scope of these notes, but it should be noted that Perfect One-Wayness is often incorrectly or implicitly assumed of cryptographic hash functions.
Another property frequently required of cryptographic hash functions is called the avalanche property: every input bit affects every output bit. If the avalance property does not hold, then some of the input structure will be reflected in the output, and this may leave the hash open to attack. One way to think about the avalanche property is to imagine the hash function taking each input bit, chopping it up, and spreading those pieces out over all the output bits.
Cryptographic hash functions are usually assumed to be collision-resistant as well as satisfying the avalanche property. Similar to the avalanche property, the output of cryptographic hash functions are also often assumed to be indistinguishable from randomness. Unlike pseudo-random functions, however, cryptographic hash functions are not keyed, so pseduo-random functions do not provide a formal basis for such an assumption. Work in the cryptographic literature on what are known as Perfectly One-Way hash functions puts this assumption on a more formal footing, but requires some changes to the hash functions. We will not discuss it further here.
One way to find collisions in hash functions is to pick random pairs until you find a collision. But this naturally requires searching most of the space, since the probability of finding a collision in a random pair is about 1/2k if 2k is the size of the input space.
But consider choosing t values and checking all pairs. Then the probability of having a collision in the set is the probability of a pair colliding times the number of pairs. Since there are t choose 2 pairs, which is about t2, you need to have about t = O(2k/2) pairs, which is only the square root of the space.
MD5 is the fifth variant of the Message Digest family of functions (a series of cryptographic hash functions designed by Ron Rivest, one of the inventors of RSA). It hashes to 128 bits, but is known to suffer from attacks on collision resistance; attacks on MD5 are known that are significantly faster than searching half the space, and more are expected to be found. For instance, see http://www.win.tue.nl/~bdeweger/CollidingCertificates for an example of two valid X.509 certificates that have a different public key but the same signature (this is possible because they rely on MD5).
The Secure Hash Algorithm family of functions is a government standard. SHA1 has an output size of 160 bits, and SHA256 and SHA512 have 256 bits and 512 bits, respectively. Some attacks on collision-resistance of SHA1 are starting to come out; they tend to employ similar inputs with well-chosen differences.
All of these hash functions (including MD5) rely on the Merkle-Damgård construction, which iterates a compression function over a sequence of fixed-length blocks. Such constructions seem to be a natural way both to scramble the data and compress it, but the family of attacks that is currently being explored exploits this structure to great advantage.
Because of these current weaknesses in hash functions, NIST (the National Institute for Standards and Technology) is holding conferences and will soon hold a competition for a new hash standard. See http://www.csrc.nist.gov/pki/HashWorkshop/index.html. The time line suggests that a new standard will be adopted around 2012.
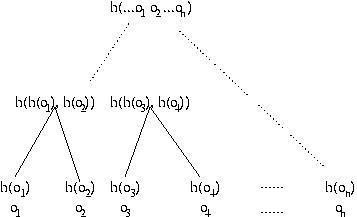
Hashes are very useful for checking authenticity of data, but sometimes the data is so large that we don't want to recompute the hash any time some small part of it changes, since computing hashes for large amounts of data is expensive. The solution is to use a Merkle hash tree, which is a tree of hash values. The data is divided into blocks, and the value of each node is the hash of the concatenation of that node's children, or the value is the hash of a block if the node is a leaf.

So instead of computing n hashes for n blocks, we compute 20 + 21 + 22 + ... + 2log(n) hashes initially (or equivalently 2*n-1) hashes). And now when we update a block, we need only update those hashes on the path from the node we updated to the root. This means that we only need to compute the height of the tree hash operations. If there are n leaf nodes, then the tree is of height log(n) + 1.
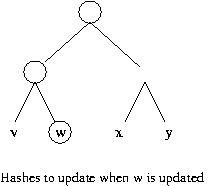
After updating block o2, why not just recompute h( h(o1), h(o2), .... h(on)) using the old values of h(oi) for all blocks but oi? This question requires a more careful accounting for the cost of invoking a hash function. This cost is linear in the number of bits of input. To simplify the exposition, suppose all the blocks consist b bits, and suppose the output of hash function h is B bits. Thus, the cost of computing the outermost invocation of h in h( h(o1), h(o2), .... h(on)) is n*B, so after updating a block, the total cost of computing a hash over all the data is n*B+b. With a Merkle hash tree, the total cost is (B*log n)+ b. Since log n is less than n, the Merkle Hash tree results in a cost savings.