Matrix multiply project
Due 2020-10-06.
Matrix multiply code base
There is a Github repository
with template code for the class. You should add your implementation
to
dgemm_mine.c,
unless you would prefer to implement in Fortran (in which case you
should send me a note and I will tell you how to proceed - you can see
dgemm_f2c.f and fdgemm.f to see the way that we can call Fortran
from C). The code in dgemm_blocked.c
dgemm_blocked.c
should give you an idea of how to think about blocking matrix
multiplication. You should not have to touch the driver matmul.c or
the plotter in plotter.py unless you want to do so, and you should
only need to touch the Makefile system if you want to adjust the C
flags (which is a good idea).
It is fine to develop on your own system, but you will want your
tuning and timing to be based off a Google E2 instance type, and that
is where I will run the code for the timing bake-off. It is also fine
to use a smaller number of test matrix sizes if you want (see the code
in matmul.c).
The competition
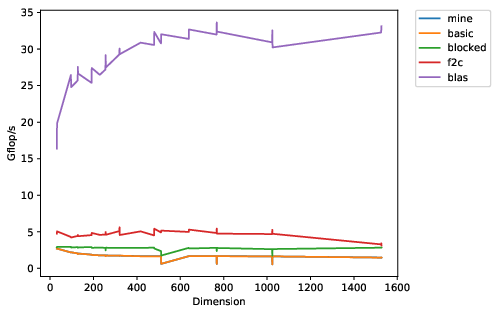
The plotting script shows you the effective single-core flop rates for
different matrix multiply routines and different matrix sizes. The
line at the top is good; that represents OpenBLAS, one of the
well-tuned BLAS libraries out there. The lines at the bottom
represent different untuned implementations. Your job is to take the
line for dgemm_mine.c and move it as high up across the board as you
can.
At the end of the project, you will get to see a plot of the performance of all the groups. Push your line as high as possible, and you get bragging rights - and a gift card to Gimme coffee, which you can redeem for either delicious coffee or delicious baked goods.
Desiderata
The objective of this assignment is to give you some experience playing with the low-level architecture and optimization ideas that we’ve discussed in the past couple weeks. It was a lot to digest in a short time, and the best way to think through these things is to try it out! Two weeks is meant to give you enough time to play with the ideas, but not enough time to get really obsessive. Remember, the goal is not really for you to produce the fastest matrix-multiply in the world; you probably won’t exceed OpenBLAS performance. Rather, the goal is to get you hands-on experience with tuning, timing, and reasoning about performance.
You have been assigned to small groups, with a variety of backgrounds represented in each group. That is deliberate. Try to find ways for all group members to be engaged! Keep in mind that not everyone in your group has the same level of background in C, Unix, etc. But not all of the work involved is programming (and this will be even more true of projects later in the course).
Recommended strategy
I recommend starting by tuning a small “kernel” multiply with
potentially fixed-size matrices. These might be odd sizes and strange
layouts; you just want them to go fast! Make sure you are looking at
matrices that are small enough so that everything fits into the lowest
levels of cache. This is important enough that it probably deserves
its own timing rig (you may want to borrow from the matmul.c code
for this). Play with different loop orders, compiler flags,
aligned memory, restrict pointers, etc. You may even decide you want
to manually use the AVX instructions! There are enough possible
variants that you may want to consider code generation or auto-tuning
strategies to explore the space of possible small multiplies available
to you.
After you have your small matrix multiplies, use a blocking strategy to build up to larger matrix multiplies. You can use the blocked code in the reference implementation as a model for how to do this. It may be worth considering ideas like copy optimization to allow you to better make use of the small kernel you developed initially. You may also want to use multiple levels of blocking associated with multiple levels of the cache hierarchy. Note that you will probably need to think a bit about how to handle edge blocks that may not be the “usual” block size.
I wrote a set of notes for this assignment a couple years ago that are still mostly relevant. There are also some pointers at the end of the code README.
Deliverables and rubric
As a group, you should submit
- A report discussing your experiments, the rationale for the tuning decisions you made, and any cool tricks that you might have found. You should connect your tuning ideas to what you have learned about vectorization and memory architecture from the class. You may use any references you find online, with appropriate citation.
- A CSV file with your timing results for the full set of matrix
sizes, run on an
n2-highcpu-2instance on GCP. This is the output ofmatmul-mine.xin the default drivers. - Your code base, either as an archive file (
zipor Uniztgzare fine) or as a pointer to a git repository that I can access. If you decide to use the git model, please make sure to give me read access to your repository (you will probably want to keep it private, otherwise).
If you have access to other machines, you may feel free to experiment with them and comment on your report, but you should not feel obliged.
As individuals, you should also provide me with an assessment of the group members (including yourselves), using this rubric. You may also give me a short description of the roles everyone played and what you think went particularly well or poorly.