CS 486: Spring 2003
Cornell University
Prof. Robert Constable

Lecture 3: Propositional Calculus

Summary of the Propositional Calculus

Restricted logical languages are designed to ignore some of the structure of propositions to concentrate on others. This is a common way of understanding a complex subject--abstract away some of the detail leaving a simpler part to analyze. In the case of the propositional calculus, we examine only the connections between propositions formed with the so-called logical connectives: and, or, implies, equivalence and not. Sometimes we also use constants for a proposition which has no proof, say False, and the proposition which needs no proof, True. An analogy from mathematics which explains our approach is the study of the algebra of integers in which we look at the arithmetic operations of plus, minus, times and the two constants with special algebraic properties, 0 and 1.

The heart of any mathematical abstraction is the idea of a variable used to define functions. In algebra the variables range over the integers, for instance; and they allow us to define functions denoted by polynomials. Variables are used to allow us to refer to functions in logic as well. In the case of logic, we are interested in the propositional functions built using the logical operators. These are denoted by propositional formulas which are like polynomials.

The propositional calculus is simple enough that we can settle many questions that are of interest for all logics. Based on a precise definition of logical truth (tautologies) and a precise notion of proof, we can decide whether a formula is true. If it is true, we can find a proof, and if it is not, we can find a counterexample to its truth. The fact that all true formulas are provable is called the completeness theorem. The fact that truth is decidable is called the decidability theorem. Their combination is the fundamental result about the calculus. We will prove it in great detail. This fundamental theorem is not true for many other logical calculi, and indeed there are many properties of this calculus that do not generalize. We will be most interested in the properties that are general.

Among the generally valid properties and generally useful concepts are the idea that the presentation of a logic involves syntax, semantics and proof mechanisms, that logical truth can be precisely defined, that proofs are systematic searches for counterexamples, that proofs can be presented in several styles, that the meaning of a formula is given by the methods of proving it, and that formulas can have several meanings. Study of this calculus reveals the ways in which computers can be used to build formulas, construct and check proofs and even find proofs, and transform them from one style to another. The fact that the connection between this formal logic of propositions and the informal logic of natural language is complex is another general result about logics, but not one that we will study in detail. Other courses do, especially in philosophy.

Labeled Disjoint Union

Definition   $l:A \; + \; r:B$   is the labeled disjoint union of sets or types A, B. We can think of this as the set of all pairs $\langle l, a \rangle, \langle r, b \rangle$ for each a $\in$ A, b $\in$ B. The labels are l and r.

Propositional Formulas are an Inductive Type

Form = var: $\!$Var + neg: Form + and: Form $\times$ Form
+ or: Form $\times$ Form + imp: Form $\times$ Form.

Discrimination is done by the case statement for F a formula.

case $F$ is
$var(v)$	$\rightarrow$	$exp(v)$
$neg(U)$	$\rightarrow$	$exp(U)$
$and(U,V)$	$\rightarrow$	$exp(U,V)$
$or(U,V)$	$\rightarrow$	$exp(U,V)$
$imp(U,V)$	$\rightarrow$	$exp(U,V)$
end

We examine how Smullyan uses the inductive character of the type of propositional formulas, which we write as Form. His account starts on page 8 under the heading Induction Principles, where he discusses definitions and proofs by induction.

For $X$ a formula, let Var$\!_X$ be the variables occurring in $X$, and let Form$\!_{X}$ be the subformulas of $X$.

Definition of Degree

We can define degree as a (primitive) recursive function as follows:

degree$(F)$ = case $F$ is
$var(v)$	$\rightarrow$	$0$
$neg(U)$	$\rightarrow$	degree$(U)+1$
$and(U,V)$	$\rightarrow$	degree$(U)+$ degree$(V)+1$
$or(U,V)$	$\rightarrow$	degree$(U)+$ degree$(V)+1$
$imp(U,V)$	$\rightarrow$	degree$(U)+$ degree$(V)+1$
end

Degree is a computable function from Form to $\Bbb{N}$; we symbolize this by: degree $\in$ Form $\rightarrow {\Bbb{N}}$.

Smullyan defines a recursive relation ``$X$ is of degree $n$.'' It is defined this way where op is one of the binary connectives, and, or, and implies.

$X$ is of degree $n$ iff

$(\exists \, V:Var.\, (F=V) \Rightarrow n=0) \hspace{.5em} \&$

$(\exists \, U:Form.\, \exists \, u: {\Bbb{N}}.\, (F=\,\sim U) \hspace{.5em} \& \hspace{.3em}$ $(U \mbox{ is of degree } u) \Rightarrow n=u+1) \hspace{.5em} \&$

$\exists \, U,V:Form.\, \exists \, u,v: {\Bbb{N}}.$

$(F=(U \mbox{ op } V)$ $\hspace{.5em} \& \hspace{.5em} (U \mbox{ is of degree } u)$ $\hspace{.4em} \& \hspace{.5em} (V \mbox{ is of degree } v))$

$\Rightarrow n=u+v+1.$

Let us also write $X$ is of degree $n$ as Degree$(X,n)$. Then we have defined Degree$(X,n)$ as a propositional function by (primitive) recursion on $X$. Another way to write the propositional function is Degree$(X)(n)$. Then we can say:

$$\mbox{Degree} \in Form \rightarrow({\Bbb{N}} \rightarrow Prop).$$

Definition of Valuation

Let $v_0$ be an interpretation of the variables in formula $X$, that is, $v_0 \in Var_X \rightarrow {\Bbb{B}}$
where ${\Bbb{B}}=${true, false}.

Let value$(v_0)(F)=$ case $F$ is
$var(v)$	$\rightarrow$	$v_0(v)$
$neg(U)$	$\rightarrow$	$not(value(v_0)(U))$
$bop(U \: op \: V)$	$\rightarrow$	$op(value(v_0)(U), \, value(x_0)(V))$
end

where the $bop$ (binary operator) case covers the operations $and,$ $or,$ $imp.$ These are operations defined on ${\Bbb{B}}$ in the usual way.

We can also define a (primitive) recursive predicate:

$Value(F,V_0,x)$ iff	$(\exists \,V:Var.(F=V) \Rightarrow x=V_0(F))$  &
	$\exists \,U,V:Form. \; \exists \,u,v: {\Bbb{B}}.$
	$(F=(U \; op \; V)$  & $Value(U,V_0,u)$  & $Value(V, V_0, u) \Rightarrow x=op\,(u,v)$

We can say that Value is a computable function of this type:

$Value \in Form \rightarrow (Var \rightarrow {\Bbb{B}}) \rightarrow ({\Bbb{B}} \rightarrow Prop).$

Smullyan does not use either of these methods exactly. He proves this theorem on page 11.

Valuation Theorem

		$\forall \, X:Form. \: \forall \, v_0:Var_X \rightarrow {\Bbb{B}}. \hspace{1em} \exists \: !f:(Form_X \rightarrow {\Bbb{B}}).$


				$\forall \, Y:Form_X [atomic(Y) \Rightarrow f(Y)=v_0(Y)$ &


						$\exists \, U:Form_X.(Y= \sim U) \Rightarrow f(Y)=not(f(U))$ &


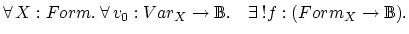
								$\exists \, U,V:Form_X.(Y=(U \; op \; V) \Rightarrow f(Y)=op(f(U),f(V)))]$

Proof by induction on $X$. Qed.

Smullyan suggests another proof in parentheses based on building a formation tree. We can prove it this way as well. Students sometimes think that the weak valuation theorem stated next captures the idea of valuations since it can be proved in such a way as to construct a valuation. It seems simpler since it does not use a recursive proposition nor does it explicitly build a recursive function; but the theorem has proofs that do not build valuations, so it does not fully describe valuations. Can you see why not?

Weak Valuation Theorem

(related to Smullyan, p. 11)

     $\forall X :$Form $. \forall v_{o} :$Var $_{X} \rightarrow {\Bbb{B}}.$

          $\forall Y :$Form $_{X}~.~ \exists !~ y~ :~ {\Bbb{B}}.$

                $\forall U, V :$ Form $_{Y}~.~ \exists ! u, v : {\Bbb{B}}$.

               (IsVar $(Y) \Rightarrow y = v_{o} (Y))~~ \&$

                [IsVar $(U) \Rightarrow u = v_{o} (U))~~ \&$

                (IsVar $(V) \Rightarrow v = v_{o} (V))~~ \&$

                 $Y = \sim U \Rightarrow~ y~ = not(u) ~~\&$

                 $Y = (U \wedge V) \Rightarrow y = and (u, v) ~~\&$

                 $Y = (U \vee V) \Rightarrow y = or (u, v) ~~\&$

                 $Y = (U \supset V) \Rightarrow y = imp (u, v) ~]$.

Proof

Let X be any formula, $v_{o}$ any interpretation, and Y any subformula of X (including X itself).

Proceed by induction on Y.

Base: Y is a variable. Then choose y to be $v_{o}(Y).$

Notice that there are no elements of Form$_{Y}$ in this case.

Induction case: Assume the theorem is true for all subformulas of Y, show that it is true for Y.

Let  U  or  U, V  be the immediate subformulas of Y. If  Y = $\sim\!$U  then by the induction hypothesis there is a unique truth value u  satisfying the conditions of the theorem. Take  y = not(u).  For any subformulas $U^{\prime}$  of  U,  there will be unique values $u^{\prime}$  in ${\Bbb{B}}$  satisfying the formula.

If Y = (U b V)  for any binany connective  b, then let u, v  be the unique truth values of U  and V  respectively, and take  y = b(u, v)  where b(u, v)  is the truth table definition of the operator b.

Qed.

Smullyan p. 11 translated

It is easily verified by induction on the degree of X (prove $\forall X :$ Form... by induction on X)

that there exists one and only one way of assigning truth values to all subformulas of X

[$\forall Y :$ Form $_{X}~.~ \exists !~ y~ :~ {\Bbb{B}}$] such that the atomic subformulas (variables) are assigned the same value

as $v_{o}~ {\em [IsVar}(Y) \Rightarrow y = v_{o} (Y)]~~$ and such that the truth value for each compound subformula Y of X

[ $\forall U, V :$ Form $_{Y}~.~ \exists ! u, v : {\Bbb{B}}$] is determined from the truth values of the immediate subformulas

of Y by the truth table rules B1 - B4 [ $Y = \sim U \Rightarrow~ y~ = not(u) ~~$ & Y = (U b V) $\Rightarrow$ y = b(u, v)].

The flaw in this reading of Smullyan is that the phrase ``there exists one and only one way of assigning truth values...'' really means that there is a function. A ``way of assigning'' is a synonym for a function.