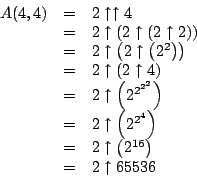- (a)
-
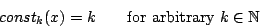
Define
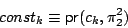
- (b)
-
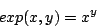
Define
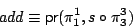
Define
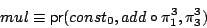
Define
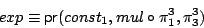
- (c)
-
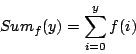
Define
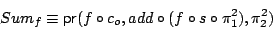
- (a)
-
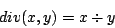
Define
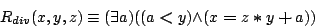
- (b)
-
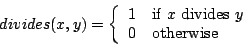
Define
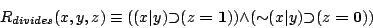
- (c)
-
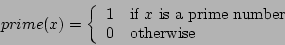
Define
![\begin{displaymath}
R_{prime}(x,z) \equiv
\begin{array}[t]{c}
({(({\forall...
...}})})}{\supset }{(z\boldsymbol{=}\mathbf{0})})
\end{array}
\end{displaymath}](img18.png)
- lemma1:
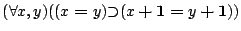
![\begin{displaymath}
\begin{array}{cll}
&
x\boldsymbol{=}y \\
\land &
...
...
\mbox{\texttt{add-base}[$y$],\texttt{subst}}
\end{array}
\end{displaymath}](img21.png)
- thm:
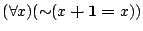
![\begin{displaymath}
\begin{array}{cll}
& &
\mbox{\texttt{base}[$x$]} \\
...
...\boldsymbol{+}\mathbf{1}$,$x$],\texttt{subst}}
\end{array}
\end{displaymath}](img22.png)
- (a)
-
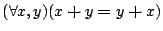
- (b)
-
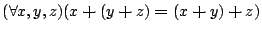
- (c)
-
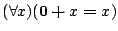
- (d)
-
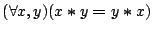
- (e)
-
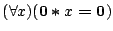
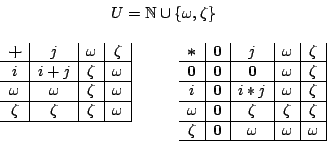
We show that the following laws are not valid in this model:
- (a)
-
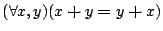
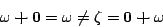
- (b)
-
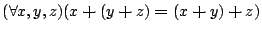
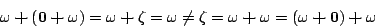
- (c)
-
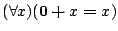
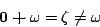
- (d)
-
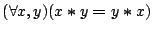
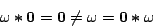
- (e)
-
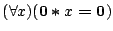
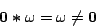
- non-surjective:

- injective:
![\begin{displaymath}
\begin{array}[t]{cl}
&
\omega\boldsymbol{+}\mathbf{1}\...
...omega \\
\supset &
x\boldsymbol{=}\omega
\end{array}
\end{displaymath}](img36.png)
![\begin{displaymath}
\begin{array}[t]{cl}
&
\zeta\boldsymbol{+}\mathbf{1}\b...
...}\zeta \\
\supset &
x\boldsymbol{=}\zeta
\end{array}
\end{displaymath}](img37.png)
- nonzero:
![\begin{displaymath}
\begin{array}[t]{cl}
&
\omega\boldsymbol{+}\mathbf{1} ...
...\boldsymbol{+}\mathbf{1}\boldsymbol{=}\zeta )}
\end{array}
\end{displaymath}](img38.png)
- add-base:

- add-step:
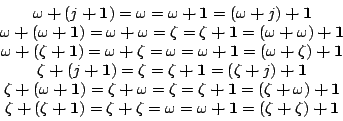
- mul-base:

- mul-step:
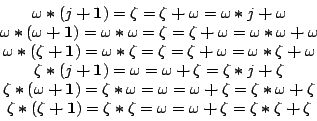
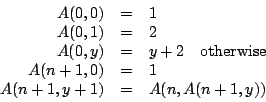
We show that
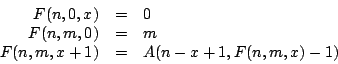
We note that the evaluation of
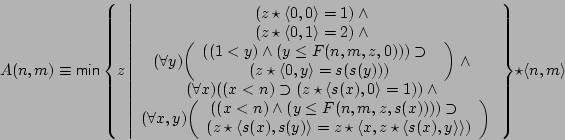
We calculate
-
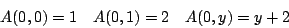
Obvious from the definition of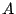 .
.
-
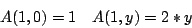
Proceed by induction on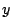 . Note
. Note 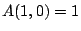 by the definition
of
by the definition
of 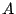 . Note
. Note
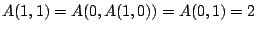 by the
definition of
by the
definition of  . Suppose
. Suppose
 for
for  . Note
. Note
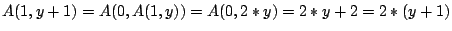 for
for 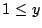 .
.
-
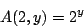
Proceed by induction on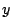 . Note
. Note 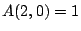 by the definition
of
by the definition
of 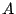 . Suppose
. Suppose 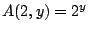 for
for 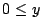 . Note
. Note
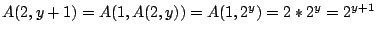 for
for 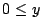 .
.
-
![\begin{displaymath}A(3, y) = 2\uparrow y =
\begin{array}[t]{c}
\underbrace{...
...dot^{\cdot^{\cdot^2}}}}} \\
\mbox{$y$\ times}
\end{array}\end{displaymath}](img75.png)
Proceed by induction on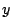 . Note
. Note 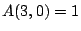 by the definition
of
by the definition
of 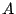 . Suppose
. Suppose
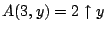 for
for 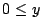 . Note
. Note
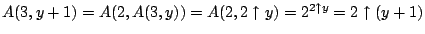 for
for 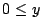 .
.
-
![\begin{displaymath}A(4, y) = 2\uparrow\uparrow y =
\begin{array}[t]{c}
\und...
...parrow(\cdots\uparrow2))} \\
\mbox{$y$\ times}
\end{array}\end{displaymath}](img79.png)
Proceed by induction on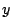 . Note
. Note 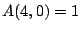 by the definition
of
by the definition
of 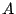 . Suppose
. Suppose
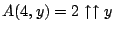 for
for 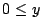 . Note
. Note
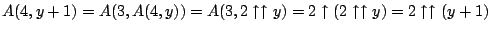 for
for 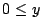 .
.