Solve the exercise on p. 24, items 1, 4, 5, and 8.
- (1)
![\begin{displaymath}
\begin{array}[t]{lccr}\mbox{(1)}&\mathsf{F}&{q}{\supset }{({...
...ox{(3)}\\
\multicolumn{4}{c}{\mathsf{X} \mbox{(2)}}\end{array}\end{displaymath}](img1.png)
- (4)
-
![\begin{displaymath}
\begin{array}[t]{lccr}\mbox{(1)}&\mathsf{F}&{[{({({p}{\supse...
...eauxAux} \end{array}}
\end{tableauxAux} \end{array}}\end{array}\end{displaymath}](img2.png)
- (5)
![\begin{displaymath}
\begin{array}[t]{lccr}\mbox{(1)}&\mathsf{F}&{{\neg }{({p}{\w...
...athsf{X} \mbox{(8)}}
\end{tableauxAux} \end{array}}\end{array}\end{displaymath}](img3.png)
- (8)
![\begin{displaymath}
\begin{array}[t]{lccr}\mbox{(1)}&\mathsf{F}&{({p}{\vee }{({q...
...lumn{4}{c}{\mbox{*}}
\end{tableauxAux} \end{array}}\end{array}\end{displaymath}](img4.png)
![\begin{displaymath}
\begin{array}[t]{lccr}\multicolumn{4}{c}{\mbox{*}}\\
\mbox{...
...thsf{X} \mbox{(11)}}
\end{tableauxAux} \end{array}}\end{array}\end{displaymath}](img5.png)
We prove that the tableaux method terminates.
We generate an analytic tableaux for the unsigned formula ![]() in the
following manner. At each stage, we have an ordered dyadic tree
in the
following manner. At each stage, we have an ordered dyadic tree
![]() , In the first stage, we construct the tree
, In the first stage, we construct the tree
![]() , a one-point tree whose origin is
, a one-point tree whose origin is ![]() .
In the
.
In the ![]() stage, we select from
stage, we select from
![]() the
left-most branch
the
left-most branch ![]() that is unclosed and incomplete. From
this branch, we consider all
that is unclosed and incomplete. From
this branch, we consider all ![]() on
on ![]() such that either
such that either
![]() or
or ![]() does not occur on
does not occur on ![]() and all
and all ![]() on
on ![]() such that neither
such that neither ![]() nor
nor ![]() occur on
occur on
![]() . We select the
. We select the ![]() or
or ![]() node that dominates all
others. If we select an
node that dominates all
others. If we select an ![]() node such that
node such that ![]() does not
occur on
does not
occur on ![]() , then extend
, then extend ![]() by
by ![]() to form
to form
![]() . If we select an
. If we select an ![]() node such that
node such that ![]() does not occur on
does not occur on ![]() , then extend
, then extend ![]() by
by ![]() to
form
to
form ![]() . If we select
. If we select ![]() node, then extend
node, then extend
![]() by
by ![]() ,
, ![]() to form
to form ![]() .
.
We show that the above method either closes or completes any branch
![]() by induction on the ``size'' of the branch. Define
by induction on the ``size'' of the branch. Define
![]() as follows:
as follows:
Note that an incomplete branch necessarily has an
Suppose
![]() . Then
. Then ![]() is closed or complete.
is closed or complete.
Suppose
![]() . Suppose an
. Suppose an ![]() node is selected.
In either one or two steps, we must close or complete
node is selected.
In either one or two steps, we must close or complete
![]() . Note
. Note
![]() because
because
![]() .
Hence, by the induction hypothesis, the method closes or completes
the branch. Suppose a
.
Hence, by the induction hypothesis, the method closes or completes
the branch. Suppose a ![]() node is selected. Then we must close
or complete
node is selected. Then we must close
or complete
![]() and
and
![]() . Note
. Note
![]() because
because
![]() ; likewise,
; likewise,
![]() because
because
![]() . Hence, by the induction hypothesis,
the method closes or completes both branches.
. Hence, by the induction hypothesis,
the method closes or completes both branches.
Hence, the method closes or completes any branch. In particular,
the method closes or completes the one-point tree whose origin is
![]() . Thus, the tableaux method terminates.
. Thus, the tableaux method terminates.
Let ![]() be a downward closed set satisfying for all
signed formulas
be a downward closed set satisfying for all
signed formulas ![]() ,
, ![]() iff
iff
![]() . We
show that
. We
show that ![]() satisfies the laws of a truth set:
satisfies the laws of a truth set:
- (0)
- Show that for any
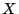 , exactly on of
, exactly on of 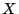 ,
, 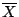 belongs
to
belongs
to 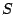 .
.
Let
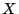 be a signed formula. If
be a signed formula. If 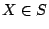 , then
, then
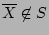 , by the definition of
, by the definition of  . If
. If 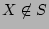 , then
, then
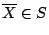 , by the definition of
, by the definition of 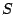 . Hence, exactly
one of
. Hence, exactly
one of 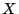 ,
, 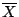 belongs to
belongs to 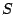 .
.
- (a)
- Show
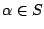 iff
iff
 and
and
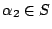 .
.
Consider
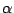 . If
. If 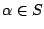 , then
, then
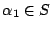 and
and
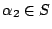 , by the definition of downward closed. Suppose
, by the definition of downward closed. Suppose
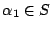 and
and
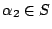 . By way of contradiction,
assume
. By way of contradiction,
assume
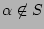 . By the definition of
. By the definition of 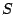 ,
,
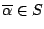 . By
. By 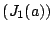 ,
,
 is some
is some 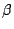 . Hence
. Hence 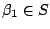 or
or 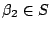 , by
the definition of downward closed. Furthermore, by
, by
the definition of downward closed. Furthermore, by 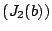 ,
,
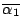 is
is 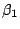 and
and
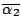 is
is
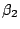 . Thus,
. Thus,
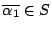 or
or
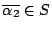 . If
. If
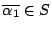 ,
then
,
then
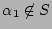 , by definition of
, by definition of 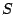 , but contrary to
the assumption. If
, but contrary to
the assumption. If
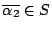 , then
, then
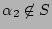 , by the definition of
, by the definition of 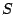 , but contrary to the
assumption. Hence
, but contrary to the
assumption. Hence 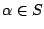 .
.
- (b)
- Show
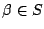 iff
iff 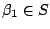 or
or 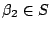 .
.
Consider
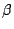 . If
. If 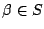 , then
, then 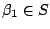 or
or
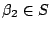 , by the definition of downward closed. Suppose
, by the definition of downward closed. Suppose
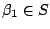 or
or 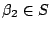 . By way of contradiction,
assume
. By way of contradiction,
assume
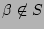 . By the definition of
. By the definition of 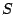 ,
,
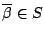 . By
. By 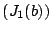 ,
,
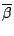 is
some
is
some 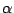 . Hence
. Hence
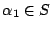 and
and
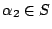 , by
the defintion of downward closed. Furthermore, by
, by
the defintion of downward closed. Furthermore, by 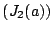 ,
,
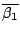 is
is 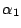 and
and
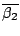 is
is
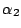 . Thus,
. Thus,
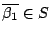 and
and
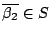 . Hence
. Hence
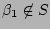 and
and
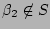 , by the defintion of
, by the defintion of 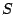 , but contrary to
the assumption. Hence,
, but contrary to
the assumption. Hence, 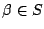 .
.
Form = var: Var +
neg: Form +
and: Form * Form +
or: Form * Form +
imp: Form * Form
Sign = t: Unit + f: Unit
Tableaux = index: Nat *
sign: Sign *
form: Form *
next: (closed: Int +
complete: Unit +
alpha: Int * Tableaux +
beta: Int * Tableaux * Tableaux)