Problem Set 11

Due Date: Thurs, May 1, 2003

Problems

1. Show that all functions that are representable in the theory $\cal Q$ are computable.

2. Let $B_1(x)$ and $B_2(x)$ be formulas in the language of $\cal Q$ with $x$ as sole free variable. Show how to construct formulas $G_1$ and $G_2$ such that

   $\models_Q$ $G_1$ $B_1(\lceil G_2 \rceil)$ and $\models_Q$ $G_2$ $B_2(\lceil G_1 \rceil)$.

3. Let $Prov$ be a provability predicate for a theory $\cal Q$ and $X$ and $Y$ be formulas in the language of $\cal Q$. Assume $\models_Q$ $Prov$($\lceil$$X$$\rceil$)$Y$ and $\models_Q$ $Prov$($\lceil$$Y$$\rceil$)$X$

   Show that both $X$ and $Y$ are theorems in $\cal Q$.

4. A pair of natural numbers $a$ and $a$ is called a stamps pair if for all $n\;{\mbox{\({{{{\geq}}}}\)}}\;a+b$ there are natural numbers $i$ and $j$ such that $n = i*3\,+\,j*5$.

   
   

   1. Prove in 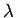-PRL that 3 and 5 is a stamps pair.

   2. Using 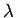-PRL notation, describe the algorithm implicitly contained in your proof.

   3. Extra credit. What other pairs of natural numbers are stamps pairs?

5. Prove in -PRL that every non-empty list of integers has a maximal element.

   l:list. ((l=[]) i:.(i l j:.(j l ji)))

   Give a -PRL definition of the predicate $i$ $l$, prove the above statement in -PRL's refinement logic, and describe the extracted algorithm in -PRL notation.