Problem Set 10

Due Date: Thurs, April 24, 2003

Problems

  1. Show how to express the following functions as $\mu$-recursive functions.


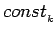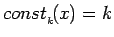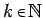
    1. The unary constant $const{\mbox{\(_{_k}\!\)}}$ with $const{\mbox{\(_{_k}\!\)}}(x)=k$ for arbitrary $k{\raisebox{0.15ex}{\(\,\scriptstyle\in\,\)}}{\mbox{\(\mathbb{N}\)}}$

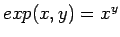
    2. Exponentiation $exp(x,y) = x^y$

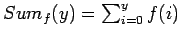
    3. Sum of a list of function values $Sum_f(y) = \sum_{i=0}^y f(i)$

    To express a function you may only use the functions $s$, $c_k$, and $\pi$$^n_i$; the operations $\circ$ (composition), pr (primitive recursion), and $\mu$ (minimization), and symbols for auxiliary functions that you prove to be $\mu$-recursive.

  2. Show how to represent the following functions in Peano Arithmetic


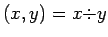
    1. Division div with div $(x,y) = x{\mbox{\(\div\)}}y$

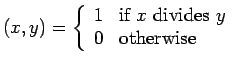
    2. The function divides with divides $(x,y) = \left\{\begin{array}{ll} 1 &\mbox{if $x$\ divides $y$}\\ 0 &\mbox{otherwise} \end{array} \right.$

    3. The function prime with prime 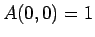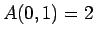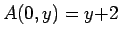$(x) = \left\{\begin{array}{ll} 1 &\mbox{if $x$\ is a prime number}\\ 0 &\mbox{otherwise} \end{array} \right.$

  3. Prove $({\mbox{\({\forall}\)}}x)(S\,x{\mbox{\({{{{\neq}}}}\)}}x)$ in Peano Arithmetic

  4. Show by providing an appropriate model that the following laws are not valid in $\cal Q$


    1. $({\mbox{\({\forall}\)}}x,y) \; (x+y = y+x)$
    2. $({\mbox{\({\forall}\)}}x,y,z) \; (x+(y+z) = (x+y)+z)$
    3. $({\mbox{\({\forall}\)}}x) \; (0 + x = x)$
    4. $({\mbox{\({\forall}\)}}x,y) \; (x*y = y*x)$
    5. $({\mbox{\({\forall}\)}}x) \; (0 * x = 0)$

  5. Extra credit. The function $A$:\(\mathbb{N}\)$^2$\(\rightarrow\)\(\mathbb{N}\) is defined recursively as follows


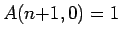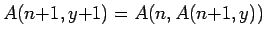
    Show that $A$ is $\mu$-recursive and calculate $A(4,4)$.


Juanita Heyerman 2003-04-18