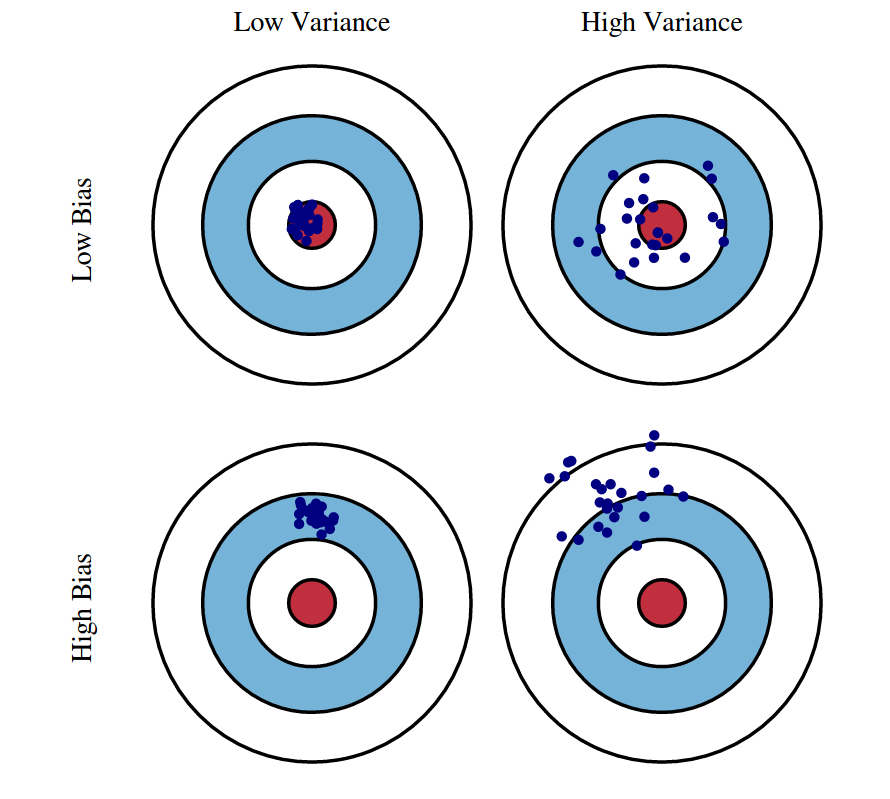
Fig 1: Graphical illustration of bias and variance.
Source: http://scott.fortmann-roe.com/docs/BiasVariance.html

Fig 1: Graphical illustration of bias and variance.
Source: http://scott.fortmann-roe.com/docs/BiasVariance.html
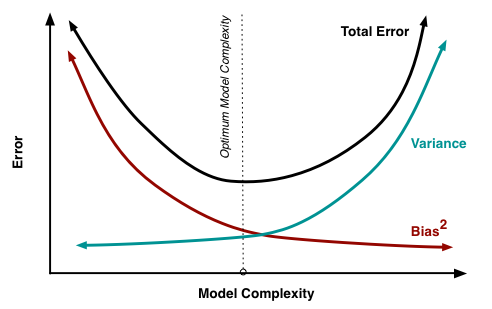
Fig 2: The variation of Bias and Variance with the model complexity. This is similar to the concept of overfitting and underfitting. More complex models overfit while the simplest models underfit.
Source: http://scott.fortmann-roe.com/docs/BiasVariance.html
The graph above plots the training error and the test error and can be divided into two overarching regimes. In the first regime (on the left side of the graph), training error is below the desired error threshold (denoted by $\epsilon$), but test error is significantly higher. In the second regime (on the right side of the graph), test error is remarkably close to training error, but both are above the desired tolerance of $\epsilon$.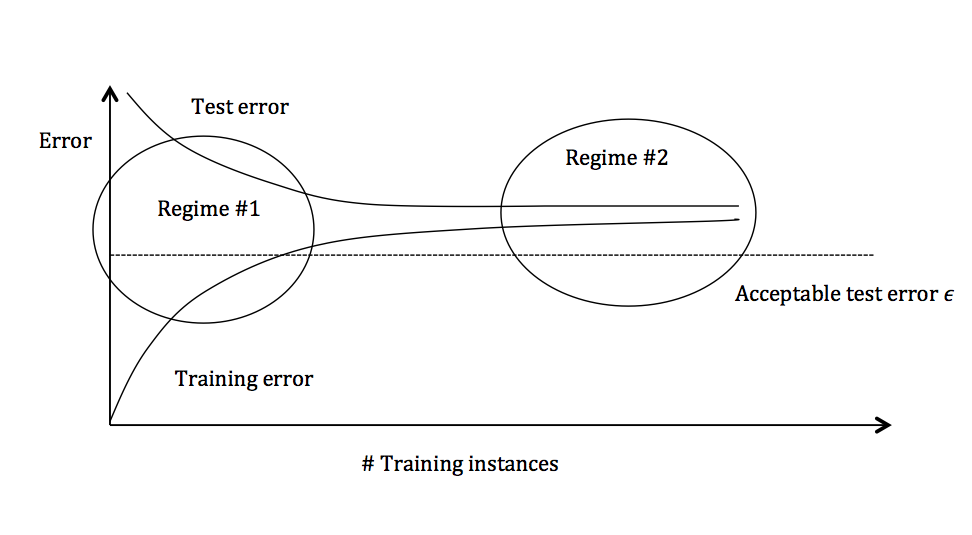
Figure 3: Test and training error as the number of training instances increases.
In the first regime, the cause of the poor performance is high variance.
Symptoms:
Remedies:
Symptoms:
Remedies: