

Binary decision tree. Only labels are stored.


Binary decision tree. Only labels are stored.
Gini impurity of a tree: \[G^T(S)=\frac{\left | S_L \right |}{\left | S \right |}G^T(S_L)+\frac{\left | S_R \right |}{\left | S \right |}G^T(S_R)\] where:
Fig: Gini Impurity Function

Fig 4: Example XOR
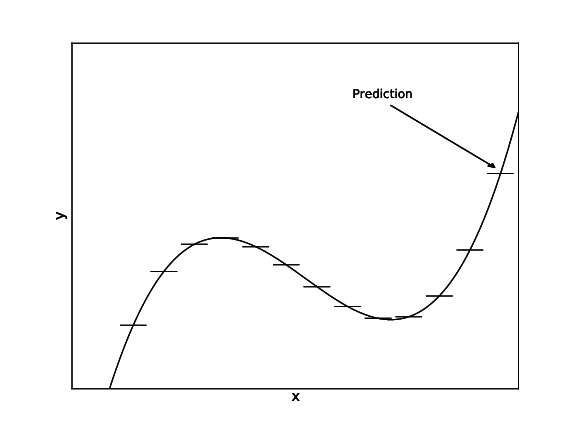
Fig: CART