Project 1 - ALU Design
CS 3410 Spring 2017
Project Due: February 17, 2017 at 11:59pm
Please submit all required documents to CMS.
You must work ALONE for this and all other individual
projects. Failure to adhere to this rule will result in an Academic
Integrity Violation. You will only be able to work in groups for
designated group projects. Updates to this assignment will be posted on
the course web page.
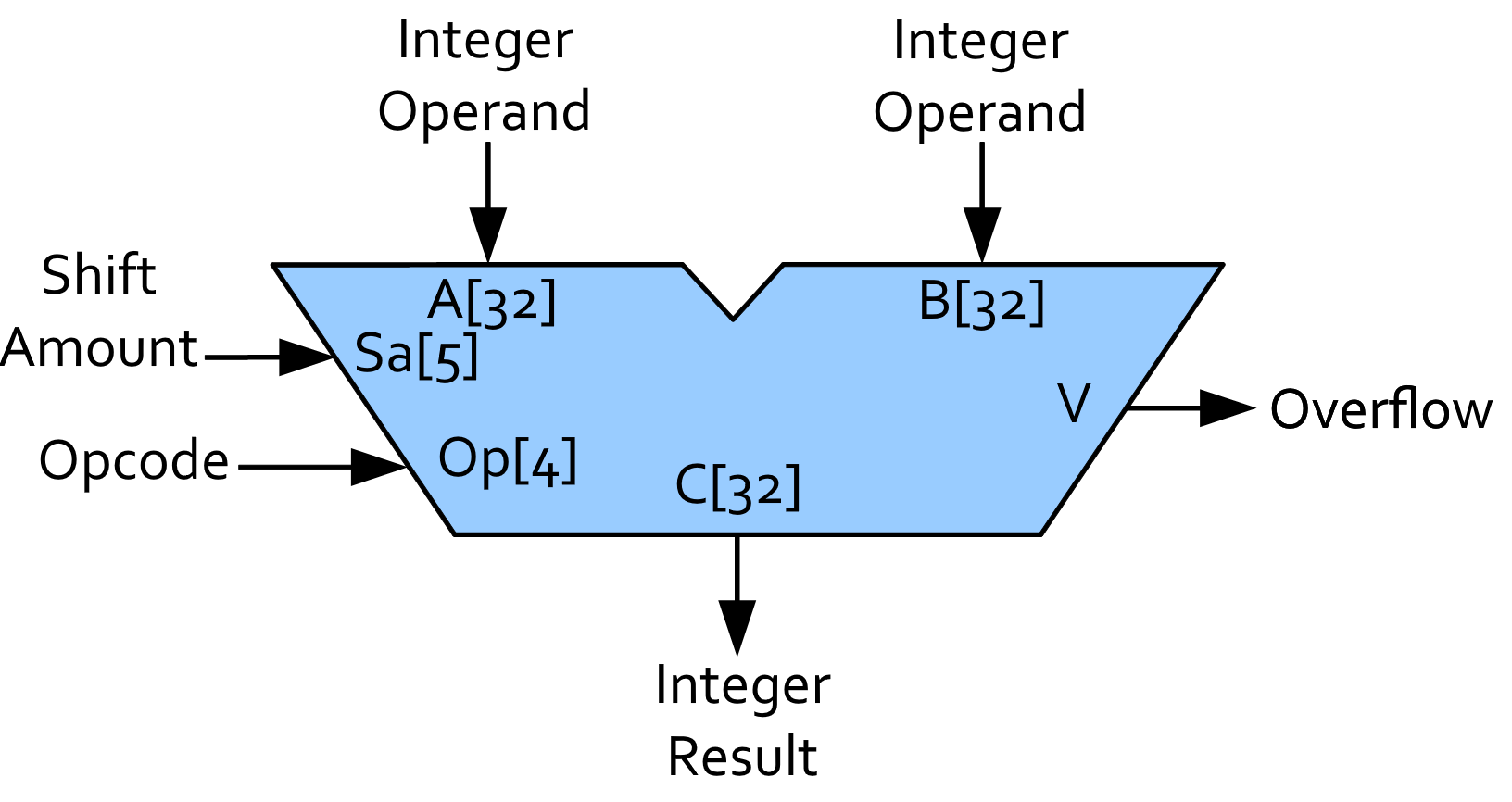
Overview
In the first four projects you will design a subset of the MIPS32 architecture in Logisim, a
software logic simulator. The goal of these projects is to move you from designing small special-purpose circuits to
building complex, general-purpose CPUs. By the end of the fourth project, you will have designed a 32-bit pipelined MIPS
CPU. For these assignments, we will ignore more advanced features, including the MIPS coprocessor instructions and
traps/exceptions.
In this project, you will design a MIPS ALU (arithmetic and logic unit) which performs all of the core computations
dictated by the assembly language. You have already seen pieces of the ALU, such as a 32-bit adder circuit, in class.
Section 3.7 of your zyBooks textbook describes a similar ALU but with a different layout than we present here.
We will be using Logisim, a free hardware design and circuit simulation tool. Logisim comes with libraries
containing basic gates, memory chips, multiplexers and decoders, and other simple components. In later assignments, you
will use many of these components to build your final CPU.
However, for this assignment you may only use the
following Logisim elements:
- Anything in the Wiring except for the resistor, constant, power, ground and transistor elements.
- Anything in the Base folder (wires, text, etc.)
- Anything in the Gates folder except for the even parity, odd parity, and controlled buffer elements
- Anything in the Plexers folder
**Important - Use this guideline for designing your circuits to avoid losing points!**
Academic Integrity. As one of the most widely studied architectures, MIPS has a wealth of information
available on the web and in textbooks. You may consult any MIPS documentation available to you in order to learn about
the instruction set, what each instruction does, how an ALU works, etc. However, we expect your design to be entirely your
own, and your submission should cite any significant sources of information you used. If you are unsure if it is okay
to borrow from some other source, just ask the TAs. If you are hesitant to ask the TAs or to cite the source, then it is
probably not okay. Plagiarism in any form will not be tolerated. It is also your responsibility to make sure your
sources match the material we describe here (warning: the top Google hit for "MIPS reference" contains several
inaccuracies).
All of the following should be subcircuits in a single Logisim circuit file. To get you started we've provided an ALU_template.circ file
with all the appropriate inputs and outputs specified.
What to Submit
- A single Logisim project file containing your ALU and all needed subcomponents. Please ensure that your circuit has no external dependencies!
- We will use Logisim's test vector function to test your circuits. In order for it to work correctly, you must ensure that the
Logisim circuits containing your solutions are named precisely "LeftShift32", "Add32", and "ALU32", and the
inputs/outputs are named "A", "B", "Op", "Sa", "C", and "V".
- A design document that details the implementation of your circuit.
- A README with your name, NetID, critical path, and gate count.
- Three text files containing your test vectors, one for each of the Left Shifter, Adder, and ALU circuits.
Circuit 1: LeftShift32
You implemented this circuit in Lab 2, but in case your design had issues, we've replicated the specification below.
The completed ALU you submit will need this piece to work.
| LeftShift32: | C = (B << Sa) | carrybits |
| Inputs: | B[32], Sa[5], Cin |
| Outputs: | C[32] |
The output C is computed by shifting B to the left Sa bits, and filling the
vacated bits on the right with carrybits, which is just Sa copies of Cin. The
shift amount Sa can be anything from 0 to 31, encoded as an unsigned integer.
Note: Some inputs and outputs are busses (as noted by the bus width in brackets); the rest are 1-bit wide.
One way to implement such a shifter is to perform the shift as a series of stages: the first stage shifts either 0 or
16 bits, the second stage either 0 or 8 bits, the third stage either 0 or 4 bits, and so on. By enabling different
combinations of stages, the circuit can shift any desired amount. Hint: Shifting a value on a 32-bit bus by a
constant amount, either left or right, is simply a matter of adding, removing, and renaming the wires on the bus, and so
requires no gates at all.
Circuit 2: Add32
| Add32: | C = A + B + Cin; V = overflow |
| Inputs: | A[32], B[32], Cin |
| Outputs: | C[32], V |
The output C is computed by adding A, B, and Cin.
A, B, and C are signed two's complement numbers. If overflow occurs, the output
V should be asserted. In such cases, the output C should correspond to the value computed if
all overflow errors are ignored. Hint: Use subcomponents to make wiring easier by building a 1-bit adder, then a 2-bit adder, then
a 4-bit adder, and so on up to 32-bits.
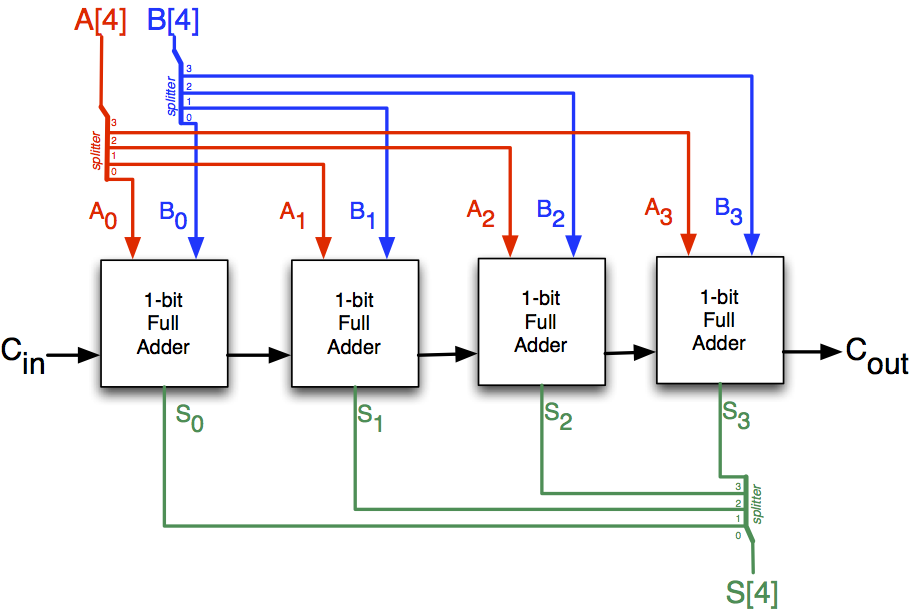
Signed vs. Unsigned Adders
There actually isn't a huge difference between signed and unsigned adders. In fact the only difference between the two is the way
that overflow is calculated. Below is a 4-bit unsigned adder, like the one you did in Lab 1...
...and here is a 4-bit two's complement signed adder.
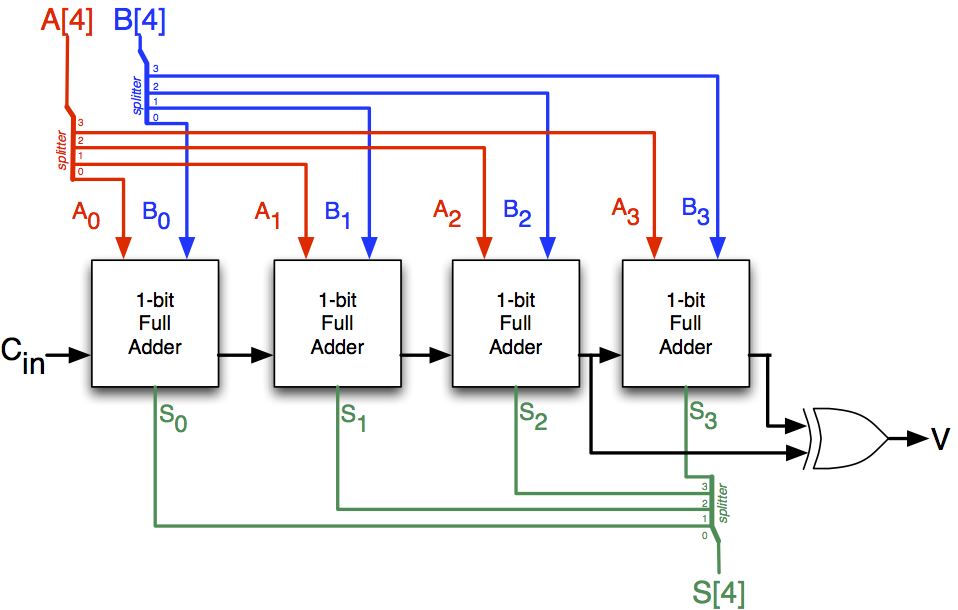
Note that the one-bit adder subcircuits in both the signed and unsigned 4-bit adders are identical (the one-bit adders are all unsigned adders).
Use this distinction when building your 32-bit signed adder.
Circuit 3: ALU32
| ALU32: | (C, V) = fOp(A, B, Sa) |
| Inputs: | A[32], B[32], Op[4], Sa[5] |
| Outputs: | C[32], V |
The C and V outputs are computed according the value of the
Op input based on the table of operations below. For the add and subtract operations, the
V output should be set to 1 if and only if the C output could be incorrect due to
a numerical overflow occurring during computation. The value C output in the presence of overflow should
correspond to the value computed if all overflow errors are ignored.
| Op | name | C | V |
|---|
| 000x | shift left logical | C = B << Sa | V = 0 |
| 001x | add | C = A + B | V = overflow |
| 0100 | shift right logical | C = B >>> Sa | V = 0 |
| 0101 | shift right arithmetic | C = B >> Sa | V = 0 |
| 011x | subtract | C = A - B | V = overflow |
| 1000 | and | C = A & B | V = 0 |
| 1010 | or | C = A | B | V = 0 |
| 1100 | xor | C = A ^ B | V = 0 |
| 1110 | nor | C = ~(A | B) | V = 0 |
| 1011 | eq | C = (A == B) ? 000...0001 : 000...0000 | V = 0 |
| 1001 | ne | C = (A != B) ? 000...0001 : 000...0000 | V = 0 |
| 1111 | gt | C = (A > 0) ? 000...0001 : 000...0000 | V = 0 |
| 1101 | le | C = (A ≤ 0) ? 000...0001 : 000...0000 | V = 0 |
An x in the opcode indicates that the circuit should not depend on the value of that bit when
determining the appropriate operation. For example, your circuit should shift left logical when the opcode is either
0000 or 0001.
The expression (test) ? 1 : 0 has a value of 1 if test is true, and 0
otherwise. In both cases, the upper 31 bits of the output are zero.
Note the difference between logical right shift (which fills with zero bits), and arithmetic right shift (which fills
the new bits with copies of the sign bit of B). The logical and (&), or
(|), xor (^), nor, and complement (~) operators are all bit-wise operations.
Don't duplicate components
Your ALU should use your adder and left shifter as components. But, as in
class, your ALU should only use a single 32-bit adder component to implement both
addition and subtraction. Similarly, your ALU should use only a single 32-bit left
shifter component to implement all of the shift operations. For instance, right
shifting can be accomplished by transforming the inputs and outputs to your
left shifter. You will be penalized if your final ALU circuit uses more than
one adder or left shifter. Of course, always strive to make your
implementation clear, but do not duplicate components in an effort to do
so.
Don't use unnecessarily large muxes
Your ALU will need to be able to select the appropriate output from your
components. Do not use a large mux as a way to select between your operations.
Foremost, some of the inputs to this large mux would be unused or duplicated which is poor
design. Additionally, larger muxes add much more complexity and gates, further increasing the critical path.
Likewise, do not use a large decoder in your design. Take some time to break this logic into
smaller, concise stages. You will be penalized if your final ALU circuit uses a large
mux (16 to 1) or decoder (4 to 16).
On specifications
It is important that your implementation of the three circuits described
above adhere to the specification in this document. Adhering to specification
is important in most all design processes, and it will also have a more
immediate effect on your grade for this lab. Automated grading will expect that
the three circuits above (and their inputs and outputs) are named
exactly as specified (case-sensitive!) and behave exactly as
specified.
Also recall that when the specification denotes a pin as A[32], the
pin should be named "A" and be 32 bits wide. The pin should not be
named "A[32]".
Design Documentation
The design document should include a diagram showing all the major components in the ALU (adder, shifter, etc.), and the datapath connections between them. For a well-designed design document, a screenshot of the Logisim circuit itself can serve as a diagram; otherwise, use the documentation to clarify and explain any parts of your circuit we might find confusing. You should provide an explanation for any more complex parts/subcomponents of your ALU.
Also include a description of your control and instruction decoding logic. For each control logic signal (or group of related control logic signals) you should provide (a) a brief description of what the signal does, e.g. what the values of the control signal mean; and (b) a truth table showing what value the signal takes for each possible opcode.
You will need to submit a design document along with your Logism project files and README via CMS by Feb 17, 2017.
Essentially, documentation provides you with another avenue of
communicating your intended design and implementation in case your
circuit has mistakes. For more help on the documentation, see
example design doc provided in your github repo (p1/design_doc.pdf).
README
In addition to the a design document, you are required to submit a short README. The README includes the following:
- Your name and NetID
- An estimate of the critical path length of the complete ALU
- An estimate of the number of gates required to implement the ALU
(including gates needed for subcomponents)
Critical Path
In synchronous logic (logic that is driven by a clock signal), the critical path is the slowest logic path in the circuit.
In Lab 1, we assumed that the operation of the ALU completes in one clock cycle. In order to determine how long the clock cycle is,
you need to figure out which path in your circuit is the longest path for the input signals to propagate through.
This particular path is called the critical path. The amount of time for the input signals to propagate through the critial path is the minimum length of one clock cycle.
The reciprocal of the clock period gives the maximum frequency of the input clock signal. You may express your critical path in terms of the number of gates in the path.
To determine the critical path you should use the following assumptions:
- Standard AND, OR, NOR, NAND, XOR, and NXOR gates have a gate delay of one unit
- NOT gates are ignored
- Multi-input and multi-bit gates have the same gate delay as their standard variants
Gate Count
In microprocessor design, gate count refers to the number of transistor switches, or gates, that are needed to implement a design.
Even with today's process technology providing what was formerly considered impossible numbers of gates on a single chip,
gate counts remain one of the most important overall factors in the end price of a chip.
Designs with fewer gates will typically cost less, and for this reason gate count remains a commonly used metric in the industry.
To determine the gate count you should use the following assumptions:
- Standard AND, OR, NOR, NAND, XOR and NXOR gates count as one gate
- NOT gates are ignored
- Multi-input gates count as a single gate
- An n-bit gate counts as n gates (the multi-bit gates logism provides aren't actually real; they are just a convenient shorthand for using a gate for each bit)
Test Vectors
Extensively testing your circuit is important to ensure correctness. Logisim, luckily, allows the use of test vectors for automated testing of circuits.
While it is not feasible to test every possible
input tuple, it is feasible in Logisim to test up to several thousand input tuples. For serious testing, you will want
to write programs (e.g. in Perl, Python, Java, Bash, etc.) to generate the test vectors.
You should strive to include enough
tuples, and to choose the tuples strategically enough, so as to exercise the
complete functionality of your circuits. Some of your tuples might be written by hand to test corner cases (e.g. adding
combinations of zero, +1, -1, max_int, min_int, etc.). Some might be generated systematically (e.g. testing every possible shift
amount, and every possible Op), and others might be generated randomly (to catch cases you didn't think
of). Testing is an important part of this project and will be graded.
For this lab, you should create three ASCII text test vector files, one for each of the Left Shifter, Adder, and ALU circuits.
These files should be formatted as Logisim test vectors (see Logisim's in-program help for the format).
A brief comment at the top of each file should indicate how the test vectors were chosen/generated.
Notes & Hints
Getting started: Design your circuits on paper before building them in Logisim. Design, then build and test
the left shifter circuit first. Next, design, build, and test a left/right shifting unit to be
used in the ALU. Think of the left/right shifter as miniature ALUs: it will have its own opcode-like control input of
your choice that selects between its different sub-operations. Repeat the same steps for circuit 2: design, build,
and test an adder/subtractor unit for use in your ALU. Then design a comparator unit that can
perform the four comparison operations by processing the output of the adder/subtractor or other subcomponents.
Finally, design, build, and test the complete ALU for circuit 3. The overall idea is to compute several potentially
needed values of the output C using the pieces you have already built and then to select the appropriate
one using a multiplexer.
Decoding logic: Your circuit will compute several values in parallel, but it will ultimately select only one for output. Your
decoding logic can often be simplified if you note that you only need the output of a sub-component to be correct (i.e.
for it to receive the correct inputs) if you know ultimately that it will be selected for output. In short, try to find
the cases where you really don't care about the inputs to, or outputs from, a sub-component.
Is optimal always best? We want you to build a good working circuit. What does good mean? It could mean speed,
readability, compactness, etc. Eventually, in later assignments, you will be asked to document your goals and
justify the choices you made. However, even if you opt for highly optimized circuits, you should make sure all of your
designs are clear and easy to follow. They should be annotated (with text labels on the circuits) for any unusual or
difficult parts of the circuit. Think and design before you implement. Laying down a very complicated circuit for
relatively simple functionality will not work in your favor during grading.
Logisim combinational analysis: Take advantage of Logisim's combinational analysis window (found under Project > Analyze Circuit), which can
automatically generate near-optimal circuits given a truth table. This only works for circuits with a few inputs, but is
very well suited to control logic.
Getting help: Ask the course staff for help. We are always available on Piazza.
Extra Credit
Although the ripple-carry adder that we designed in Lab 1 and covered in lecture is easy to teach and reason about, in practice it is far too
slow to be used in a real processor. A much faster and more effective design is the carry-lookahead adder which trades off a
high gate count for a vastly lower critical path. Some of the specifics of this approach are covered in
Section 24.5 of your textbook, and there are also a number of excellent online resources on the topic.
Particularly adventurous students who endeavour to optimize their critical path by building a carry-lookahead adder of
one sort or another will be rewarded with extra credit. Please note, however, that it is essential that your design must work.
Building a working CLA is significantly more difficult than building a working ripple adder, and every term, a few
students set out to do it and end up with no working adder at all. Don't let this happen to you!
Frequently Asked Questions
Logisim
- Q: How does component xxx work in Logisim?
-
We have had many questions asking about how to use a particular component in Logisim. In general, the help file in Logisim has explained things very well. You can access the help file from the 'Help' menu in Logisim. You could either search by keyword or browse the entire reference from the left pane.
- Q: How to create a sub-circuit in Logisim?
-
Please refer to Sub-circuit creation.
- Q: How to build a one-bit adder?
-
Logisim has a very nice feature for editing truth table and generating the corresponding logic circuit. You could refer to the following pages Edit truth table and Generate Circuit for an explanation.
The following steps have worked well:
- Place the desired input and output nodes in the canvas.
- Save the changes to the canvas.
- Right Click on the symbol that represents the current canvas in the explorer pane, and select 'Analyze Circuit' to bring up the 'Combinantional Analysis' window
- Edit the truth table and Generate the circuit
- Q: How does this multiplexer thing work?
-
It takes multiple inputs and selects one of them based on the control signal. For instance, suppose I have 4 inputs into the multiplexer in the following order: 1, 2, 3, 4. Since we have 4 inputs, our control needs 2 bits (base 2 log of the number of inputs) to determine the output of the multiplexer. In this particular case, the mapping would be: 00 => 1, 01 => 2, 10 => 3, 11 => 4.
Shift and overflow
- Q: Should our adder perform unsigned or two's complement addition? What is the difference?
- What is the difference, indeed?
- Q: How to do right shift with left shifter?
-
Hint: You need to manipulate the input bits before passing them to the left shifter, e.g. transform the input bits to an intermediate format, pass the input through the left shifter, and then do a reverse-transformation to get your result.
- Q: My overflow bits are buried within my 16-bit adders! How am I supposed to XOR the carry-in and carry-out of the MSB?
-
You could either add a few extra outputs to your adders and only use
them for the MSB, or you could detect overflows the alternate way: If
the sign bit of the two inputs is the same but different from the
output, you have an overflow.
Critical Path
- Q: What is a critical path?
-
In synchronous logic (logic that is driven by a clock signal), the critical path is the slowest logic path in the circuit. In lab 1, we assumed
that the operation of the ALU completes in one clock cycle. In order to determine how long the clock cycle is, you need to figure out which path in your
circuit is the longest path for the input signals to propagate through. This particular path is called the critical path. The amount of time for the
input signals to propagate through the critial path is the minimum length of one clock cycle. The reciprocal of the clock period gives the maximum
frequency of the input clock signal.
- Q: What is gate count?
-
In microprocessor design, gate count refers to the number of transistor switches, or gates, that are needed to implement a design.
Even with today's process technology providing what was formerly considered impossible numbers of gates on a single chip,
gate counts remain one of the most important overall factors in the end price of a chip. Designs with fewer gates will typically cost less,
and for this reason gate count remains a commonly used metric in the industry.
Testing
Q: How do we test our circuits?
The Cornell version of Logisim adds a special "Test Vector" feature to
Logisim for automated testing of circuits. The documentation for this is
accessed from within Logisim: select Help->User's Guide from the toolbar. On
the left pane of the help window that appears, look for and select the item
labeled "Test Vectors".
Q: How do we comment our test vector files?
# starts a comment.
Q: To write a test case for my test vector, I need to know what the correct result for a certain operation is. How could I ever do this?
All of the ALU's operations are clearly defined arithmetic operations. The results can easily be computed by hand. Even better, implementations of these arithmetic operations are available in every major programming language.
Q: We can just use Logisim's logging feature to generate a test vector, right?
Let's get this straight. To verify the correctness of your ALU, you are going to log the output of your ALU for a few inputs, and then you are going to verify that your ALU gives the same output when given those same inputs?
This is basically asking "does your ALU produce the same outputs as your ALU?"
The first rule of tautology club is the first rule of tautology club.


