Problem Set 1: SML Warm-up

Due Wednesday, January 31, 2007, 11:59 pm.

---

The goal of this problem set is to get you started with the SML language. If you are not already familiar with SML, it may be a fair amount of new material, and you will need to figure out how to use the SML software. So please begin early.

Instructions

This problem set has four parts. You will write your solution to each part in a separate file: part1.sml, part2.sml, part3.sml, and part4.sml. To get you started, we have provided stub files that you can download from CMS. Please write your name and NetID as a comment at the top of each file. In SML, comments are written (*like this*). Once you have finished, submit your solution using CMS.

Three important notes about grading

1. Compile errors: All programs that you submit must compile. Programs that do not compile will receive an automatic zero. If you are having trouble getting your assignment to compile, please visit consulting hours. If you run out of time, it is better to comment out the parts that do not compile and hand in a file that compiles, rather than handing in a more complete file that does not compile.
2. Missing functions: We will be using an automatic grading script, so it is crucial that you name your functions and order their arguments according to the problem set instructions, and that you place the functions in the correct files. Do not break this rule.
3. Code style: Finally, please pay attention to style. Refer to the CS 312 style guide and lecture notes; we expect you to stick to the formatting guidelines of the style guide. Poor style will count against your grade. Take the extra time to think out the problems and find the most elegant solutions before coding them up.

---

Part 0: Newsgroup

Post a message with your NetID in the subject to the cornell.class.cs312.talk newsgroup.

Note that the main course newsgroup is cornell.class.cs312 (without the talk), where you should not post this particular message. However, if you have questions about assignments (including this one) or the course in general, you should post to the main course newsgroup. (And we highly encourage the use of this newsgroup as a medium to get your questions answered.)

Part 1: Basic Functions

1. Write a function catalan: int -> int where catalan(n) gives the n^th Catalan number C_n. Here is the Wikipedia page that explains what a Catalan number is. You will find there several strategies for computing C_n; choose whichever method you like best. Make sure your solution is correct by checking your output with the Catalan numbers provided on the page.
2. Write a function days: {month:int, day:int, year:int} * int -> {year:int, days:int}. The first argument is a record that holds a date with a 2-digit year; the second is a 4-digit reference year (it doesn't have to be 4 digits, but it will be a full, unabbreviated year).

   The job of this function is to convert that 2-digit year into a fully specified year which falls within a range of -74 to +25 years from the reference year. For example, if the reference year is 2007, then all 2-digit years must represent something in the range 1933 to 2032 (1933 being 74 years less than 2007, and 2032 being 25 more). This range uniquely identifies any 2-digit year.

   The output should be a record with the full four-digit year, and the number of days from the beginning of the year until the specified month and day. The number of days may depend on whether it's a leap year. Note that the rules for leap years in the (standard) Gregorian calendar are more complicated than most people realize.

   For example, when the function is applied to the pair ({month=1, day=1, year=7},2006), the result should be {days=0, year=2007}. And when applied to ({month=3, day=1, year=0}, 1910), the result should be {days=59, year=1900}. (This is a change from the original problem spec. If you correctly implement the original spec, that is ok too.)
3. Write a function isSorted: int list -> bool that given a list of integers returns true if the list is sorted in non-descending order, and false otherwise. (Consider the empty list to be sorted. Try not to sort a copy of the list and then compare it with the original.)
4. Write a function normalize: string -> string that will remove excess spaces from a given string and capitalize the first (and only the first) letter of each word. Any sequence of non-space characters is considered a word. There should be exactly one space between any two words, and no leading or trailing spaces. For example:

   normalize "  dOn't TyPe l1ke  7HIs,  EVER! !! " = "Don't Type L1ke 7his, Ever! !!"

   You should browse the SML Basis Library for functions that might be of help to you here.

Part 2: Expressions and Types

Give the types of the following expressions.

1. (op +, true orelse false, [#"#"])

2. fun f(x::xs) = if (x = 0) then xs else []

3. fun g(a, b, c) = case a of
                      [] => (round c) = 1
                    | 1::xs => not (null xs)
                    | _ => b

4. let
     fun foo(a, b) = a b
     fun bar(z) = {x = 1, y = ""}
   in
     foo (foo, (bar, bar))
   end

For each of the following types, give an expression with that type. In addition, make sure each expression is bound to a variable or function name. (Note that strictly speaking, these names are not really "variables.")

5. real list * string * (int * int -> bool)

6. (char * int * (string -> int)) list list

In each of the following, replace ??? with a value that will make the whole expression evaluate to 42.

7. let
     val zardoz = ???
   in
     if (#1 (#2 zardoz)) then (#2 (#1 zardoz)) else ~42
   end

8. let
     fun zardoz(x) =
     let
       fun prod(y) = case y of
                       y::ys => y * prod(ys)
                     | [] => 1
     in
       prod(length(x)::x)
     end
   in
     zardoz(???)
   end

Part 3: Binding and Scope

For each of the following cope snippets, rename each variable, including function parameters, by appending a distinct number to it. (We suggest you start with 1 and work your way up the natural numbers.) Then at the point where each identifier goes out of scope—i.e., is no longer visible—add a comment of the form (*end scope: x1*). If more than one variable goes out of scope at the same point, you can put them all in the same comment, separated by commas.

For example, change

let
  val x = nil
in
  x
end

to

let
  val x1 = nil
in
  x1
end (*end scope: x1*)

1. fun area(r) =
   let
     val r = r * r
   in
     Math.pi * r
   end

2. let
     val x = 3
     fun f(z) = x
   in
     let
       fun g(z) =
       let
         val x = 4
       in
         f(z)
       end
     in
       (g(), f())
     end
   end

Part 4: Datatypes

In this problem, you will write some functions that work on binary trees. The datatype that we will use to represent our trees is this:

datatype tree = Null | Node of int * tree * tree

Each node in these trees will store an integer value, and Null represents the empty tree. The first tree in each Node (right after the int) is the left subtree, and the second is the right subtree.

Here are two example trees and how you would specify them using this datatype:

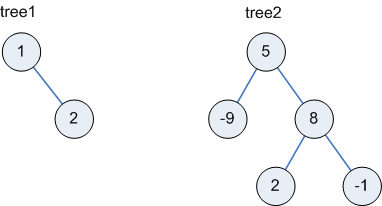
val tree1 = Node(1, Null, Node(2, Null, Null))
val tree2 = Node(5,
                 Node(~9, Null, Null),
                 Node(8,
                      Node(2, Null, Null),
                      Node(~1, Null, Null)))

Note that tree2 could have been specified on a single line, but judicious use of linebreaks and proper indentation help make the code a lot more readable.

1. Write a function inOrder: tree -> int list that given a binary tree returns the list of integers in that tree according to an in-order traversal of the tree. Using our examples above, you should get

   inOrder tree1 = [1, 2]
   inOrder tree2 = [~9, 5, 2, 8, ~1]

2. Define the sum of a tree to be the sum of all the integers in that tree. Write a function maxSubtreeSum: tree -> tree * int that given a tree will return:
   • the subtree within this tree which has the greatest sum over all possible subtrees, and
   • the sum of this maximal subtree.

   Notes: The empty tree is a subtree of any tree, and we define its sum to be 0. You can break ties arbitrarily if more than one subtree has the maximal sum. A subtree is defined only by where it starts; it always extends from that point on down to the leaves—you can't cut it short. The original tree itself is a possible subtree. (If you are wondering why the whole tree won't always give you the maximum sum, remember that integers can be negative.)

   For our two example trees, your function should give

   maxSubtreeSum tree1 = (Node(1, Null, Node(2, Null, Null)), 3)
   maxSubtreeSum tree2 = (Node(8, Node(2, Null, Null), Node(~1, Null, Null)), 9)

---