In recitation we talked a bit about graphs: how to represent them and how to traverse them. Today we will discuss one of the most important graph algorithms: Dijkstra's shortest path algorithm, a greedy algorithm that efficiently finds shortest paths in a graph. (Pronunciation: "Dijkstra" is Dutch and starts out like "dike").
Many more problems than you might at first think can be cast as shortest path problems, making this algorithm a powerful and general tool. For example, Dijkstra's algorithm is a good way to implement a service like MapQuest that finds the shortest way to drive between two points on the map. It can also be used to solve problems like network routing, where the goal is to find the shortest path for data packets to take through a switching network. It is also used in more general search algorithms for a variety of problems ranging from automated circuit layout to speech recognition.
Let's start by defining a data abstraction for weighted, directed graphs so we can express algorithms independently of the implementation of graphs themselves. In a weighted graph, each of its edges has a nonnegative weight that we can think of as the distance one must travel when going along that edge.
(* A signature for directed graphs. The signature is * simplified by not explicitly representing edges as * type. *) signature WGRAPH = sig type graph (* A directed graph comprising a set of * vertices and directed edges with nonnegative * weights. *) type vertex (* A vertex, or node, of the graph *) (* Whether two vertices are the same vertex. *) val eq: vertex*vertex->bool (* All vertices in the graph, without any duplicates. * Run time: O(|V|). *) val vertices: graph->vertex list (* outgoing(v) is a list of pairs (v_i,w_i), one for each * edge leaving the vertex v. For each index i, the * corresponding edge leaves v and goes to v_i, and * has weight w_i. * Run time is linear in the length of the result. *) val outgoing: vertex->(vertex*int) list end
There are some constraints on the running time of certain operations in this specification. Importantly, we assume that given a vertex, we can traverse the outgoing edges in constant time per edge. Some graph implementations do not have these properties, but we can easily write an almost trivial implementation that does:
structure Graph : WGRAPH = struct (* Note: vertex must contain a ref to allow graphs * containing cycles to be built and to give vertices * a notion of unique identity (ref identity). * The type vertex must be a datatype to permit it to * be defined recursively. *) datatype vertex = V of (vertex*int) list ref type graph = vertex list fun eq(V(v1), V(v2)) = (v1 = v2) fun vertices(g) = g fun outgoing(V(lr)) = !lr end
A path through the graph is a sequence (v1, ..., vn) such that the graph contains an edge e1 going from v1 to v2, an edge e2 going from v2 to v3, and so on. That is, all the edges must be traversed in the forward direction. The length of a path is the sum of the weights along these edges e1,..., en-1. We call this property "length" even though for some graphs it may represent some other quantity: for example, money or time.
To implement MapQuest, we need to solve the following shortest-path problem:
Given two vertices v and v', what is the shortest path through the graph that goes from v to v' ? That is, the path for which summing up the weights along all the edges from v to v' results in the smallest sum possible.
It turns out that we can solve this problem efficiently by solving a more general problem, the single-source shortest-path problem:
Given a vertex v, what is the length of the shortest path from v to every vertex v' in the graph?
It is this problem that we will investigate in this lecture.
The single-source shortest path problem can also be formulated on an undirected graph; however, it is most easily solved by converting the undirected graph into a directed graph with twice as many edges, and then running the algorithm for directed graphs. There are other shortest-path problems of interest, such as the all-pairs shortest-path problem: find the lengths of shortest paths between all possible source–destination pairs. The Floyd-Warshall algorithm is a good way to solve this problem efficiently.
Let's consider a simpler problem: solving the single-source shortest path problem for an unweighted directed graph. In this case we are trying to find the smallest number of edges that must be traversed in order to get to every vertex in the graph. This is the same problem as solving the weighted version where all the weights happen to be 1.
Do we know an algorithm for determining this? Yes: breadth-first search. The running time of that algorithm is O(V+E) where V is the number of vertices and E is the number of edges, because it pushes each reachable vertex onto the queue and considers each outgoing edge from it once. There can't be any faster algorithm for solving this problem, because in general the algorithm must at least look at the entire graph, which has size O(V+E).
We saw in recitation that we could express both breadth-first and depth-first search with the same simple algorithm that varied just in the order in which vertices are removed from the queue. We just need an efficient implementation of sets to keep track of the vertices we have visited already. A hash table fits the bill perfectly with its O(1) amortized run time for all operations. Here is an imperative graph search algorithm that takes a source vertex v0 and performs graph search outward from it:
(* Simple graph traversal (BFS or DFS) *) let val q: queue = new_queue() val visited: vertexSet = create_vertexSet() fun expand(v: vertex) = let val neighbors: vertex list = Graph.outgoing(v) fun handle_edge(v': vertex): unit = if not (member(visited,v')) then ( add(visited, v'); push(q, v') ) else () ) in app handle_edge neighbors end in add(visited, v0); expand(v0); while (not (empty_queue(q)) do expand(pop(q)) end
This code implicitly divides the set of vertices into three sets:
Except for the initial vertex v0, the vertices in set 2 are always neighbors
of vertices in set 1. Thus, the queued vertices form a frontier in the graph,
separating sets 1 and 3. The expand function moves a frontier
vertex into the completed set and then expands the frontier to include any
previously unseen neighbors of the new frontier vertex.
pop
function, which selects a vertex from a queue. If q is a FIFO queue, we
do a breadth-first search of the graph. If q is a
LIFO queue, we do a depth-first search.
If the graph is unweighted, we can use a FIFO queue and keep track of the number of edges
taken to get to a particular node. We augment the visited set to keep track
of the number of edges traversed from v0; it becomes a hash table
implementing a map from vertices to edge counts (ints). The only modification
needed is in expand, which adds to the frontier a newly found vertex at a
distance one greater than that of its neighbor already in the frontier.
(* unweighted single-source shortest path *) let val q: queue = new_queue() val visited: vertexMap = create_vertexMap() (* visited maps vertex->int *) fun expand(v: vertex) = let val neighbors: vertex list = Graph.outgoing(v) val dist: int = valOf(get(visited, v)) fun handle_edge(v': vertex) = case get(visited, v') of SOME(d') => () (* d' <= dist+1 *) | NONE => ( add(visited, v', dist+1); push(q, v') ) in app handle_edge neighbors end in add(visited, v0, 0); expand(v0); while (not (empty_queue(q)) do expand(pop(q)) end
Now we can generalize to the problem of computing the shortest path
between two vertices in a weighted graph. We can solve this problem by making minor
modifications to the BFS algorithm for shortest paths in unweighted graphs. As
in that algorithm, we keep a visited map that maps vertices to their distances
from the source vertex v0. We change
expand so that Instead of adding 1 to the
distance, its adds the weight of the edge traversed. Here is a first cut at an
algorithm:
let val q: queue = new_queue() val visited: vertexMap = create_vertexMap() fun expand(v: vertex) = let val neighbors: vertex list = Graph.outgoing(v) val dist: int = valOf(get(visited, v)) fun handle_edge(v': vertex, weight: int) = case get(visited, v') of SOME(d') => if dist+weight < d' then add(visited, v', dist+weight) else () | NONE => ( add(visited, v', dist+weight); push(q, v') ) in app handle_edge neighbors end in add(visited, v0, 0); expand(v0); while (not (empty_queue(q)) do expand(pop(q)) end
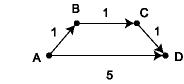
This is nearly Dijkstra's algorithm, but it doesn't work. To see why, consider the following graph, where the source vertex is v0 = A.

The first pass of the algorithm will add vertices B and D to the map visited,
with distances 1 and 5 respectively. D will then become part of the completed
set with distance 5. Yet there is a path from A to D with the shorter length 3.
We need two fixes to the algorithm just presented:
SOME case a check is needed to see whether the path just discovered
to the vertex v' is an improvement on the previously discovered path (which
had length d)pop(q) should be a
priority queue extract_min operation that removes the vertex with the
smallest distance.
increase_priority(q,v) that increases the priority of an element v
already in
the queue q. This new operation is easily implemented for heaps
using the same bubbling-up algorithm used when performing heap insertions.With these two modifications, we have Dijkstra's algorithm:
(* Dijkstra's Algorithm *) let val q: queue = new_queue() val visited: vertexMap = create_vertexMap() fun expand(v: vertex) = let val neighbors: vertex list = Graph.outgoing(v) val dist: int = valOf(get(visited, v)) fun handle_edge(v': vertex, weight: int) = case get(visited, v') of SOME(d') => if dist+weight < d' then ( add(visited, v', dist+weight); incr_priority(q, v', dist+weight) ) else () | NONE => ( add(visited, v', dist+weight); push(q, v', dist+weight) ) in app handle_edge neighbors end in add(visited, v0, 0); expand(v0); while (not (empty_queue(q)) do expand(pop(q)) end
There are two natural questions to ask at this point: Does it work? How fast is it?
Each time that expand is called, a vertex is moved from the
frontier set to the completed set. Dijkstra's algorithm is an example of a
greedy algorithm, because it just chooses the closest frontier vertex at every
step. A locally optimal, "greedy" step turns out to produce the global
optimal solution. We can see that this
algorithm finds the shortest-path distances in the graph example above, because
it will successively move B and C into the completed set, before D, and thus D's
recorded distance has been correctly set to 3 before it is selected by the
priority queue.
The algorithm works because it maintains the following two invariants:
For every completed vertex, the recorded distance (in visited) is the shortest-path distance to that vertex from v0.
For every frontier vertex v, the recorded distance is the shortest-path distance to that vertex from v0, considering just the paths that traverse only completed vertices and the vertex v itself. We will call these paths internal paths.
We can see that these invariants hold when the main loop starts, because the only completed vertex is v0 itself, which has recorded distance 0. The only frontier vertices are the neighbors of v0, so clearly the second part of the invariant also holds. If the first invariant holds when the algorithm terminates, the algorithm works correctly, because all vertices are completed. We just need to show that each iteration of the main loop preserves the invariants.
Each step of the main loop takes the closest frontier vertex v and promotes it to the completed set. For the first invariant to be maintained, it must be the case that the recorded distance for the closest frontier vertex is also the shortest-path distance to that vertex. The second invariant tells us that the only way it could fail to be the shortest-path distance is if there is another, shorter, non-internal path to v. Any non-internal path must go through some other frontier vertex v'' to get to v. But this path must be longer than the shortest internal path, because the priority queue ensures that v is the closest frontier vertex. Therefore the vertex v'' is already at least as far away than v, and the rest of the path can only increase the length further (note that the assumption of nonnegative edge weights is crucial!).
We also need to show that the second invariant is maintained by the loop.
This invariant is maintained by the calls to incr_priority and push
in handle_edge. Promoting v to the completed set may create new internal
paths to the neighbors of v, which become frontier vertices if they are
not already; these calls ensure that the recorded distances to these neighbors
take into account the new internal paths.
We might also be concerned that incr_priority could be called on
a vertex that is not in the priority queue at all. But this can't happen because
incr_priority is only called if a shorter path has been found to a
completed vertex v'. By the first invariant, a shorter path cannot exist.
Notice that the first part of the invariant implies that we can use Dijkstra's algorithm a little more efficiently to solve the simple shortest-path problem in which we're interested only in a particular destination vertex. Once that vertex is popped from the priority queue, the traversal can be halted because its recorded distance is correct. Thus, to find the distance to a vertex v the traversal only visits the graph vertices that are at least as close to the source as v is.
Every time the main loop executes, one vertex is extracted from the queue.
Assuming that there are V
vertices in the graph, the queue may contain O(V)
vertices. Each pop operation takes O(lg V)
time assuming the heap implementation
of priority queues. So the total time required to execute the main loop itself
is O(V lg V). In addition, we must consider the time spent in the function expand,
which applies the function handle_edge to each outgoing edge.
Because expand is only called once per vertex, handle_edge
is only called once per edge. It might call push(v'), but there can
be at most V
such calls during the entire execution, so the total cost of that
case arm is at most O(V lg V). The other case arm may be called
O(E) times,
however, and each call to increase_priority takes O(lg
V)
time with
the heap implementation. Therefore the total run time is O(V
lg V + E lg V),
which is O(E lg V) because V
is O(E) assuming a connected graph.
(There is another more complicated priority-queue implementation called a Fibonacci
heap that implements increase_priority in O(1)
time, so that the
asymptotic complexity of Dijkstra's algorithm becomes O(V
lg V + E); however,
large constant factors make Fibonacci heaps impractical for most uses.)