Induction is a method of proving statements about inductively defined sets. A set is inductively defined when it is generated from some base elements using some set of constructor operations.
The most common example of an inductively defined set is the set of nonnegative integers N={0,1,2,...}, also called the natural numbers. This set can be generated from the base element 0 and the successor function inc, where inc(x) = x+1. Induction over the natural numbers is often called mathematical induction.
There are many inductively defined sets other than the natural numbers, such as lists, trees, and ML expressions. Later in the semester we will look at induction over such sets. This type of induction is often called structural induction, but the principle is the same.
Induction is an example of logical abstraction. It essentially allows us to do infinitely many concrete arguments in a single abstract argument. This is very similar to the idea of functional abstraction. Recall that after getting tired of typing the expressions 3*3 ... 16*16 ... e*e ... 27717*27717 ... BIG-HAIRY-EXPRESSION*BIG-HAIRY-EXPRESSION etc., we packaged up the common part of these expressions using functional abstraction:
fun square(x:int):int = x*x
In a sense, square packages up infinitely many potential computations x*x in a single finite box.
Now we can do the same sort of abstraction with logical arguments. For example, suppose we had no built-in integer multiplication and had to build it using addition. Consider the following recursive program for multiplying nonnegative integers:
fun mult(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)
In arguing that this program is correct, we might go through the following thought process:
mult(A, 0) ==> (fun(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)) (A, 0) ==> if 0=0 then 0 else A+((fun(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)) (A, 0-1)) ==> 0
mult(A, 1) ==> (fun(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)) (A, 1) ==> if 1=0 then 0 else A+((fun(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)) (A, 1-1)) ==> A+((fun(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)) (A, 0)) ==> A+0; ==> A
mult(A, 2) ==> (fun(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)) (A, 2) ==> if 2=0 then 0 else A+((fun(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)) (A, 2-1)) ==> A+((fun(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)) (A, 1)) ==> A+A; ==> 2A
mult(A, 3) ==> (fun(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)) (A, 3) ==> if 3=0 then 0 else A+((fun(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)) (A, 3-1)) ==> A+((fun(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)) (A, 2)) ==> A+2A; ==> 3A
and so on, ad nauseam.
Now note that the argument for the base case 0 is different, but after that the arguments all look the same. It's only the numbers that are different. Using logical abstraction, we can do all these infinitely many cases at once.
mult(A, B) ==> (fun(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)) (A, B) ==> if B=0 then 0 else A+((fun(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)) (A, B-1)) ==> A+((fun(m:int, n:int):int = if n=0 then 0 else m+mult(m, n-1)) (A, B-1)) ==> A+(B-1)A ==> AB
Note that we were able to make this argument purely symbolically, by using a symbol B to stand for any positive number, without knowing what B is. The argument is therefore valid for any B > 0. We could in principle string these arguments together to get up as high as we like.
The induction principle says that in order to prove that a property is true of all natural numbers, it suffices to do the following:
One way to think about mathematical induction is that it allows us to show that we can climb as far as we want on a ladder, by first showing that we can get on the bottom rung (the basis), and then showing that if we have gotten to some rung (any rung), then we can get to the next one (the induction step). In effect induction provides us with infinitely many results by doing only a finite amount of work (although it may seem like an infinite amount of work when you are first learning how!).
In a proof by induction, we first show that the statement is true for the "smallest" values of our inductively defined set, which for the natural numbers is just 0. This is the basis. We then want to show that the statement holds for any arbitrary n > 0. We don't get to assume anything about n except that it is positive, but we do get to assume that the statement holds for all values less than n. This part of the argument is called the induction step. The assumption that the statement holds for all values less than n is called the induction hypothesis.
Once we have done these things, we are done: the induction principle allows us to conclude that the property is true for all n.
Here is a simple example of the use of induction. We want to prove that the sum of the first n squares is n(n+1)(2n+1)/6.
The expression
is mathematical shorthand for "the sum for i running from 0 to n of i2", or
02 + 12 + 22 + ... + n2
We wish to show that this property is true for all n. The variable we will do induction on is k.
and we wish to prove
We break this expression up in such a way that allows us to use the induction hypothesis. In this case, this means expressing the sum as the sum of (1) the first k terms and (2) the last (k+1st) term:
By the induction principle, we may now conclude that the property holds for all n>=0.
Let us show that for the set G={8,9,10,...}, each element of G is a sum of 3's and 5's. (Mathematically we say that these integers are a "linear combination" of 3 and 5.)
The variable we are doing induction on is n.
The property we are trying to prove is that for every n in the set G={8,9,10,...}, there exist nonnegative integers u and v such that n = 3u + 5v.
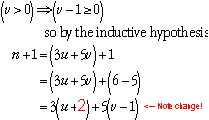
On the other hand, if v = 0, then u >= 3, because the
smallest number in G is 8. Then in this case we get
n+1 = 3(u-3) + 5*2, so we can take u' = u-3 and v' =
2.
Recursion and induction are closely related. Induction is often used to show that a recursive procedure computes the correct answer. We saw one example of this above.
This use of induction relies on the substitution model and mathematical induction. Consider the following function fact for computing n! = n(n-1)(n-2)...2 1.
fun fact(n:int):int = if n=1 then 1 else n*fact(n-1)
We will do induction on A, where A stands for any positive integer.
The property we wish to prove is
fact(1) ==> (fun fact(n:int):int = if n=1 then 1 else n*fact(n-1)) 1 ==> if 1=1 then 1 else 1*((fun fact(n:int):int = if n=1 then 1 else n*fact(n-1)) 0) ==> 1
so we are done with the basis.
fact(A+1) ==> (fun fact(n:int):int = if n=1 then 1 else n*fact(n-1)) (A+1) ==> if (A+1)=1 then 1 else (A+1)*((fun fact(n:int):int = if n=1 then 1 else n*fact(n-1)) A) ==> (A+1)*((fun fact(n:int):int = if n=1 then 1 else n*fact(n-1)) A) ==> (A+1)*A! <-- here we used the induction hypothesis ==> (A+1)!
In general we will not require proofs that contain this much detail. The level of detail in this example illustrates, however, that the process is quite mechanical, and could in principle be performed by a machine. The automatic verification of programs (checking that they meet a given specification) is an active area of research.